HDU 2722 Here We Go(relians) Again (最短路)

题目链接

Problem Description

The Gorelians are a warlike race that travel the universe conquering new worlds as a form of recreation. Given their violent, fun-loving nature, keeping their leaders alive is of serious concern. Part of the Gorelian security plan involves changing the traffic patterns of their cities on a daily basis, and routing all Gorelian Government Officials to the Government Building by the fastest possible route.

Fortunately for the Gorelian Minister of Traffic (that would be you), all Gorelian cities are laid out as a rectangular grid of blocks, where each block is a square measuring 2520 rels per side (a rel is the Gorelian Official Unit of Distance). The speed limit between two adjacent intersections is always constant, and may range from 1 to 9 rels per blip (a blip, of course, being the Gorelian Official Unit of Time). Since Gorelians have outlawed decimal numbers as unholy (hey, if you're the dominant force in the known universe, you can outlaw whatever you want), speed limits are always integer values. This explains why Gorelian blocks are precisely 2520 rels in length: 2520 is the least common multiple of the integers 1 through 9. Thus, the time required to travel between two adjacent intersections is always an integer number of blips.

In all Gorelian cities, Government Housing is always at the northwest corner of the city, while the Government Building is always at the southeast corner. Streets between intersections might be one-way or two-way, or possibly even closed for repair (all this tinkering with traffic patterns causes a lot of accidents). Your job, given the details of speed limits, street directions, and street closures for a Gorelian city, is to determine the fastest route from Government Housing to the Government Building. (It is possible, due to street directions and closures, that no route exists, in which case a Gorelian Official Temporary Holiday is declared, and the Gorelian Officials take the day off.)

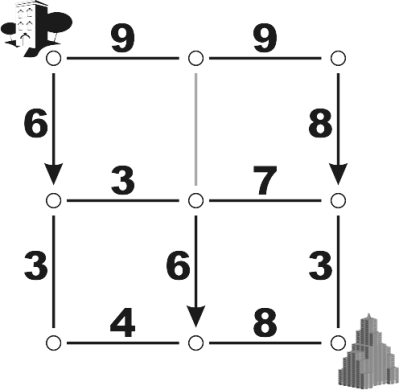
The picture above shows a Gorelian City marked with speed limits, one way streets, and one closed street. It is assumed that streets are always traveled at the exact posted speed limit, and that turning a corner takes zero time. Under these conditions, you should be able to determine that the fastest route from Government Housing to the Government Building in this city is 1715 blips. And if the next day, the only change is that the closed road is opened to two way traffic at 9 rels per blip, the fastest route becomes 1295 blips. On the other hand, suppose the three one-way streets are switched from southbound to northbound (with the closed road remaining closed). In that case, no route would be possible and the day would be declared a holiday.

Input

The input consists of a set of cities for which you must find a fastest route if one exists. The first line of an input case contains two integers, which are the vertical and horizontal number of city blocks, respectively. The smallest city is a single block, or 1 by 1, and the largest city is 20 by 20 blocks. The remainder of the input specifies speed limits and traffic directions for streets between intersections, one row of street segments at a time. The first line of the input (after the dimensions line) contains the data for the northernmost east-west street segments. The next line contains the data for the northernmost row of north-south street segments. Then the next row of east-west streets, then north-south streets, and so on, until the southernmost row of east-west streets. Speed limits and directions of travel are specified in order from west to east, and each consists of an integer from 0 to 9 indicating speed limit, and a symbol indicating which direction traffic may flow. A zero speed limit means the road is closed. All digits and symbols are delimited by a single space. For east-west streets, the symbol will be an asterisk '*' which indicates travel is allowed in both directions, a less-than symbol '<' which indicates travel is allowed only in an east-to-west direction, or a greater-than symbol '>' which indicates travel is allowed only in a west-to-east direction. For north-south streets, an asterisk again indicates travel is allowed in either direction, a lowercase "vee" character 'v' indicates travel is allowed only in a north-to-south directions, and a caret symbol '^' indicates travel is allowed only in a south-to-north direction. A zero speed, indicating a closed road, is always followed by an asterisk. Input cities continue in this manner until a value of zero is specified for both the vertical and horizontal dimensions.

Output

For each input scenario, output a line specifying the integer number of blips of the shortest route, a space, and then the word "blips". For scenarios which have no route, output a line with the word "Holiday".

Sample Input

2 2

9 * 9 *

6 v 0 * 8 v

3 * 7 *

3 * 6 v 3 *

4 * 8 *

2 2

9 * 9 *

6 v 9 * 8 v

3 * 7 *

3 * 6 v 3 *

4 * 8 *

2 2

9 * 9 *

6 ^ 0 * 8 ^

3 * 7 *

3 * 6 ^ 3 *

4 * 8 *

0 0

Sample Output

1715 blips

1295 blips

Holiday

分析：

有个n*m大小的矩形，起点在矩形的左上角， 终点在右下角， 里面一个小矩形代表一个街区（block)。

每个小矩形的边长都是2520， 小矩形的边有一个速度限制，范围是0～9， 如果是0表示这条边不能行驶。

关于输入部分，由上到下，从左到右，按照上图的对应的位置方式给出数据，

每一条边是 "数字"+“空格”+“符号”的形式，

数字表示这条边的限速，符号表示这条路是单向（还分东西， 南北）的还是双向的。

其实主旨思想就是在求一个最从左上角到右下角的最短路，关键就在于确定每一个点对应的编号，以及每一条路所对应的起点和终点。

每行输入的奇数行肯定是表示的横向的路径，路径条数就是列数，偶数行表示的是竖向的路径，路径条数就是列数+1，这些就没必要解释了把。

然后是确定每一个点所对应的编号：

对于横向的路径，第i行的第j个点所对应的编号就是(m+1)(i/2)+j，所连接的另一个点编号就是该点的编号加1、减1

而对于纵向的路径，第i行的第j个点所对应的编号就是(m+1)(i/2-1)+j，所连接的另一个点编号就是该点的编号加m、减m。

这样就完全把路径给保存下来了。

代码：

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<queue>
#include<utility>
using namespace std;
const int INF = 0x3f3f3f3f;
int n,m,u,w;
int  num;//一共涉及到的点的数目
char str[150];
const int vNum=445;
const int eNum=vNum*vNum/2;
int Count;
typedef pair<int,int>pii;
struct Node
{
    int to,val;
    int Next;
}node[eNum];
int head[vNum];
int dis[vNum];
struct Node1
{
    int len,num;
};
void add(int u,int v,int w)
{
    node[Count].to=v;
    node[Count].val=w;
    node[Count].Next=head[u];
    head[u]=Count;
    Count++;
}
void spfa(int src)
{
    for(int i=1;i<=num;i++)
        dis[i]=INF;
    dis[src]=0;
    queue<Node1>q;
    Node1 Now,Next;
    Now.len=dis[src];
    Now.num=src;
    q.push(Now);
    while(!q.empty())
    {
        Now=q.front();
        q.pop();
        int u=Now.num;//得到点
        if(dis[u]!=Now.len)continue;
        for(int i=head[u];i!=-1;i=node[i].Next)
        {
            int v=node[i].to;
            int temp=dis[u]+node[i].val;
            if(dis[v]>temp)
            {
                dis[v]=temp;
                Next.len=dis[v];
                Next.num=v;
                q.push(Next);
            }
        }
    }
}
int main()
{
    while(~scanf("%d%d",&n,&m)&&n&&m)
    {
        getchar();
        Count=0;
        num=(n+1)*(m+1);//最后一个点的标号
        memset(head,-1,sizeof(head));
        for(int i=1; i<=2*n+1; i++)//对于n行的图形，那么一共需要输入的路径就有2*n+1行
        {
            gets(str);
            int len=strlen(str);
            if(i&1)//输入的是行的信息
            {
                for(int j=0,k=1; j<len; j+=4,k++) //数字、空格、方向、空格四个一个循环
                {
                    u=(m+1)*(i/2)+k;//一个点对应的一个编号
                    w=str[j]-'0';//获得速度
                    if(w==0) continue;
                    if(str[j+2]=='*')//双向的
                    {
                        add(u,u+1,2520/w);
                        add(u+1,u,2520/w);
                    }
                    else if(str[j+2]=='<')//单向的从右到左
                    {
                        add(u+1,u,2520/w);
                    }
                    else//单向的从左到右
                    {
                        add(u,u+1,2520/w);
                    }
                }
            }
            else//输入的是列的信息
            {
                for(int j=0,k=1; j<len; j+=4,k+=1)
                {
                    u=(m+1)*(i/2-1)+k;//每次上面的那个点代表的数字
                    w=str[j]-'0';
                    if(w==0)continue;
                    if(str[j+2]=='*')//双向的
                    {
                        add(u,u+m+1,2520/w);
                        add(u+m+1,u,2520/w);
                    }
                    else if(str[j+2]=='v')//从上到下
                    {
                        add(u,u+m+1,2520/w);
                    }
                    else if(str[j+2]=='^')//从下到上
                    {
                        add(u+m+1,u,2520/w);
                    }
                }
            }
        }
        spfa(1);
        if(dis[num]!=INF)
            printf("%d blips\n",dis[num]);
        else
        printf("Holiday\n");
    }
    return 0;
}