沉迷AC自动机无法自拔之：穿越广场 square

如标题所言，我已经沉迷于AC自动机无法自拔了。。。

这又是一道AC自动的题，红红火火恍恍惚惚

穿越广场

[问题描述]

L 国的仪仗队要穿越首都广场了。首都广场可以看做是一块 N*M 的矩形网格,仪仗队要从左上角的格点(0,0)行进到右下角的格点(N,M),行进过程中只能向右走或者向下走。如果把向右走记为’R’,把向下走记为’D’,则仪仗队的行进序列是一个包含 M 个’R’和 N 个’D’的字符串。

这时,L 国的首长又提出了一个奇葩的要求。他认为仪仗队行走的序列中必须包含他给出的两个字符串。请你计算一下,满足首长要求的行进序列有多少种呢?

[输入]

第一行一个整数 T,表示数据组数。

每组数据的第一行是两个整数 M，N，表示行进序列由 M 个’R’ 和 N 个’D’ 构成。

每组数据的第二行和第三行是两个不相同的字符串,表示首长要求这两个字符串是行进序列的子串。

[输出]

一个整数,表示满足要求的行进序列的数量模 1000000007 的值

[输入输出样例]

Input

2

3 2

RRD

DDR

3 2

R

D

Output

1

10

[数据说明]

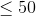对于 50% 的数据，，字符串长度，T=1；

对于 100% 的数据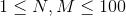，，字符串由’R’、’D’组成且长度，；

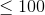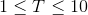首先，部分分怎么搞咧，哎呀这不是重点，用 kmp+dp xjb搞一下就好了嘛，我要讲的是AC自动机

好的，满分算法，AC自动机上dp。

先讲一下做法：将给出的两个串建成AC自动机，然后在这个建好的AC自动机上跑dp，根据题目要求，路径需要包含给出的两个字符串，也就是说，在AC自动机上跑的时候需要经过两个叶子节点。我们设状态 f[i][j][k][0/1/2/3] 为，当前走了 i 步，其中有 j 步为 R ，当前走到的节点为 k ，两个叶子节点的经过情况为后面的0/1/2/3时的方案数。

这时有转移：

　　f[i+1][j+1][ son[k]['R'] ][ l' ]+=f[i][j][k][l];

　　f[i+1][j][ son[k]['D'] ][ l' ]+=f[i][j][k][l];

　　,,

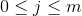当 son[k]['R']（son[k]['D']）为单词末尾时，l'=l |（1<<x(该单词编号，可以是0或1)），否则 l'=l；

所以最后的答案为：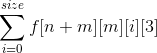

下面是代码，注意，这题有一点很坑，它是先输的 M 再输的 N，我因为这个调了好久。。。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define mod (1000000007)
#define ll long long
#define il inline
#define RG register
using namespace std;
il int gi(){ RG int x=0,q=1; RG char ch=getchar(); while( ( ch<'0' || ch>'9' ) && ch!='-' ) ch=getchar();
  if( ch=='-' ) q=-1,ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-48,ch=getchar(); return q*x; }
il void File(){freopen("square.in","r",stdin); freopen("square.out","w",stdout);}

int T,n,m;
char s[110];

struct Trie{
   int son[210][2],fail[210],size,root;
   int val[210];
   il void init(){
      size=1;root=0;
      memset(f,0,sizeof(f));
      memset(son,0,sizeof(son));
      memset(val,0,sizeof(val));
      memset(fail,0,sizeof(fail));
   }

   il int idx(char c){ return c=='D'; }

   il void insert(char *s,int q){
      RG int cur=root;
      for(RG int i=0;s[i];i++){
         RG int id=idx(s[i]);
         if(!son[cur][id]) son[cur][id]=size++;
         cur=son[cur][id];
      }
      val[cur]|=1<<q; return ;
   }

   il void build(){
      int que[1010];
      RG int hd=0,tl=0;
      for(RG int i=0;i<2;i++)
         if(son[root][i]){
            que[tl++]=son[root][i];
            fail[son[root][i]]=root;
         }
         else son[root][i]=root;

      while(hd<tl){
         RG int cur=que[hd++];
         for(RG int i=0;i<2;i++){
            RG int Son=son[cur][i];
            if(Son){
               RG int f=fail[cur];
               while(f && !son[f][i]) f=fail[f];
               fail[Son]=son[f][i];
               val[Son]|=val[fail[Son]];
               que[tl++]=Son;
            }
            else son[cur][i]=son[fail[cur]][i];
         }
      }
   }

   ll f[210][110][210][4];//当前走了i步，其中有j步是R，现在在k这个节点，两种字符串的出现情况是l
   il void dp(){
      f[0][0][0][0]=1;
      for(RG int i=0;i<n+m;i++)
         for(RG int j=0;j<=m;j++)
            for(RG int k=0;k<size;k++)
               for(RG int l=0;l<4;l++)
                  if(f[i][j][k][l])
                     for(RG int t=(j==m);t<2;t++){
                        RG int Son=son[k][t];
                        RG int jj=j+(t==0);
                        RG int ss=l|val[Son];
                        (f[i+1][jj][Son][ss]+=f[i][j][k][l])%=mod;
                     }
      RG ll ret=0;
      for(RG int i=0;i<size;i++) (ret+=f[n+m][m][i][3])%=mod;
      printf("%lld\n",ret);
   }

}AC;

il void init(){
   m=gi(),n=gi(); AC.init();
   scanf("%s",s); AC.insert(s,0);
   scanf("%s",s); AC.insert(s,1);
   AC.build();
}

il void work(){ AC.dp(); }

int main(){ File(); T=gi(); while(T--){ init(); work(); } return 0; }