P1155 双栈排序

题目描述

Tom最近在研究一个有趣的排序问题。如图所示，通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

操作aaa

如果输入序列不为空，将第一个元素压入栈S1​

操作b

如果栈S1不为空，将S1栈顶元素弹出至输出序列

操作c

如果输入序列不为空，将第一个元素压入栈S2​

操作d

如果栈S2不为空，将S2​栈顶元素弹出至输出序列

如果一个1−n的排列P可以通过一系列操作使得输出序列为1,2,…,(n−1),n，Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”，而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列：<a,c,c,b,a,d,d,b>

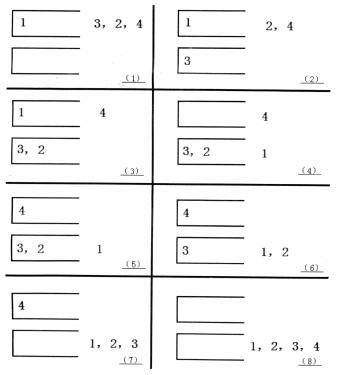
当然，这样的操作序列有可能有几个，对于上例(1,3,2,4)，<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

输入输出格式

输入格式：

第一行是一个整数n。

第二行有n个用空格隔开的正整数，构成一个1−n的排列。

输出格式：

共一行，如果输入的排列不是“可双栈排序排列”，输出数字0；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

输入输出样例

输入样例#1：

4
1 3 2 4

输出样例#1：

a b a a b b a b

输入样例#2：

4
2 3 4 1

输出样例#2：

0

输入样例#3：

3
2 3 1

输出样例#3：

a c a b b d

说明

30%的数据满足： n≤10

50%的数据满足：n≤50

100%的数据满足： n≤1000

Solution：

　　本题二分图染色+栈模拟。　　

　　若我们知道每个数应该放在哪个栈中，就可以去模拟了。

　　考虑数$a_i,a_j,a_k$不能在同一栈的情况，若$i<j<k,a_i<a_j,a_i>a_k$那么$i,k$是肯定不能在同一栈内的，我们对二元组建边，那么就是个二分图染色的模型了。

　　由于要字典序最小，所以每次染色时另当前未被染色的位置为栈1再去dfs，染色后每个位置所在的栈就确定了。

　　然后就是纯模拟咯。

　　（安利一个神奇的调试技巧：用iostream库下的cerr代替cout，在评测机测试时会直接跳过这条输出语句，但在终端可以输出，这样就能防止忘记删调试语句而写挂！>.^_^.<）

代码：

/*Code by 520 -- 9.5*/
#include<bits/stdc++.h>
#define il inline
#define ll long long
#define RE register
#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)
using namespace std;
const int N=;
int n,a[N],minn[N],col[N];
int to[N],net[N],h[N],cnt;
int stk1[N],stk2[N],top1,top2;

il void add(int u,int v){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt;}

bool dfs(int u){
    for(RE int i=h[u];i;i=net[i])
        if(!col[to[i]]) {
            col[to[i]]=col[u]^;
            if(!dfs(to[i]))return ;
        }
        else if(col[to[i]]==col[u]) return ;
    return ;
}

int main(){
    ios::sync_with_stdio();
    cin>>n,minn[n+]=0x7fffffff;
    For(i,,n) cin>>a[i];
    Bor(i,,n) minn[i]=min(minn[i+],a[i]);
    For(i,,n) For(j,i+,n) if(a[i]>minn[j+]&&a[i]<a[j]) add(i,j),add(j,i);
    For(i,,n) if(!col[i]) {
        col[i]=;
        if(!dfs(i))cout<<,exit();
    }
    For(i,,n) cerr<<col[i]<<' ';cerr<<endl;
    int cnt=;
    For(i,,n){
        if(col[i]==) stk1[++top1]=a[i],cout<<"a ";
        else stk2[++top2]=a[i],cout<<"c ";
        while(top1&&stk1[top1]==cnt||top2&&stk2[top2]==cnt){
            if(stk1[top1]==cnt) cout<<"b ",--top1;
            else cout<<"d ",--top2;
            ++cnt;
        }
    }
    return ;
}