一、下载安装Turbo C++

我安装的是Turbo C++ 3.2.2.0下载链接

二、画图

1.打开Turbo C++，点击右下角start turbo C++

2.点击file ->new

3.输入代码

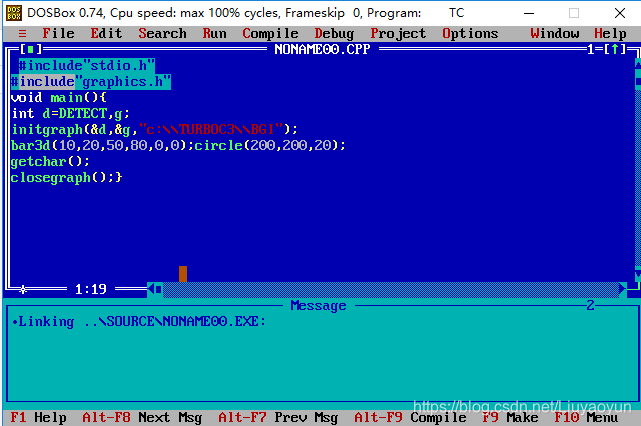
4.编译运行，如下图所示

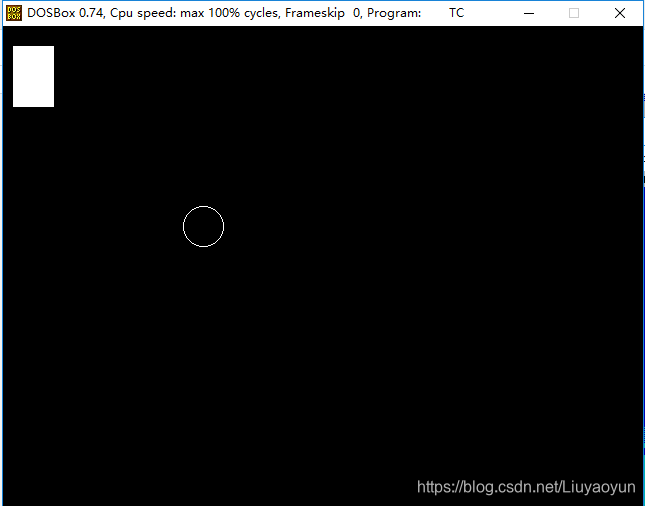
//为什么不试试用DEV呢 逃~

计算机图形学中使用Turbo C++画图步骤的更多相关文章

  1. Mathematics for Computer Graphics数学在计算机图形学中的应用 [转]

    最近严重感觉到数学知识的不足! http://bbs.gameres.com/showthread.asp?threadid=10509 [译]Mathematics for Computer Gra ...

  2. 3D游戏与计算机图形学中的数学方法-四元数

    说实话关于四元数这一节真的是不好懂,因为里面涉及到好多数学知识,单说推出来的公式就有很多.不怕大家笑话,对于四元数的学习我足足花了两天的时间,包括整理出这篇文章.在前面一章我写到了“变换”,这也是总结 ...

  3. 3D游戏与计算机图形学中的数学方法-变换

    1变换 在3D游戏的整个开发过程中,通常需要以某种方式对一系列的向量进行变换.通常用到的变换包括平移,缩放和旋转. 1.1通用变换 通常可将n x n可逆矩阵M看成是一个从坐标系到另一个坐标系的变换矩 ...

  4. 3D游戏与计算机图形学中的数学方法-点线面

    <易传·系辞上传>:”易有太极,是生两仪,两仪生四象,四象生八卦.” 借用一下古代先人们的智慧引一下本文的主题-三维图形中的点线面,在三维几何中也有一句话可以和上面的话相对应:由点成线,由 ...

  5. 3D游戏与计算机图形学中的数学方法-视截体

    视截体用来表示一个空间的范围,位于这个空间范围内的三维场景的任何物体都可以被看到. 视截体由六个平面围成,其中的四个平面与场景的边界相对应,分别被称为左,右,底,顶视截面.另外两个平面称为近视截面和远 ...

  6. 关于opengl中的矩阵平移，矩阵旋转，推导过程理解 OpenGL计算机图形学的一些必要矩阵运算知识

    原文作者:aircraft 原文链接:https://www.cnblogs.com/DOMLX/p/12166896.html 为什么引入齐次坐标的变换矩阵可以表示平移呢? - Yu Mao的回答 ...

  7. 随机L系统分形树 分类： 计算机图形学 2014-06-01 23:27 376人阅读 评论(0) 收藏

    下面代码需要插入到MFC项目中运行,实现了计算机图形学中的L系统分形树. class Node { public: int x,y; double direction; Node(){} }; CSt ...

  8. 计算机图形学课件pdf版

    为方便大家学习,我将自己计算机图形学的课件分享. 下载链接:http://pan.baidu.com/s/1kV5BW8n 密码:eqg4 注:本课件与教材配套PPT有所不同.教材配套PPT是编写教材 ...

  9. [计算机图形学]Blinn-Phong光照模型

    目录 一.前言 二.原理 三.代码 一.前言 Blinn-Phong光照模型以Phong模型为基础的,提供比Phong更柔和.更平滑的高光,而且由于Blinn-Phong的光照模型省去了计算反射光线的 ...

随机推荐

  1. CSS 解决Float后塌陷问题

    当父级元素没有设定高度时候,而子集元素设定float类型时候,此时父级元素不能靠子集元素撑起来,所以就形成了塌陷: 示例分析 **1.Float之前的效果** <!DOCTYPE html> ...

  2. javascript输出数据到文件

    function export(name, data) { var urlObject = window.URL || window.webkitURL || window var export_bl ...

  3. print函数与转义字符

    一.print函数 作用:1.输出数字. print(520) 2.输出字符串.(注意:输出字符串要添加单引号.双引号或三引号,告诉编译器可直接输出,不用分析) print('you are so b ...

  4. export html to canvas image

    export html to canvas image canvas.toDataURL https://developer.mozilla.org/en-US/docs/Web/API/HTMLCa ...

  5. HTMLMediaElement.srcObject & URL.createObjectURL & HTMLMediaElement.src

    HTMLMediaElement.srcObject & URL.createObjectURL & HTMLMediaElement.src Uncaught TypeError: ...

  6. js 实现各种算法 APP

    js 实现各种算法 APP 常见算法: 排序,搜索/查找,枚举,遍历,最短路径,二叉树 open source web app desktop app react native app flutter ...

  7. css var all in one & html & root & :root

    css var all in one number :root{ --num: 0; } html{ --num: 0; } let html = document.querySelector(`ht ...

  8. Axios & POST & application/x-www-form-urlencoded

    Axios & POST & application/x-www-form-urlencoded application/x-www-form-urlencoded https://g ...

  9. vue components registration & vue error & Unknown custom element

    vue components registration & vue error & Unknown custom element vue.esm.js:629 [Vue warn]: ...

  10. ts 索引签名 无视多余的属性类型

    interface SquareConfig { color?: string; width?: number; [propName: string]: any; } function asd(opt ...