CF 板刷总结

CF 板刷总结

这件事的开始要从万圣节那一天说起。当然，万圣节只用于描述时间，我显然是不参加任何万圣节活动的对吧。

以下是一些我觉得有必要拿出来讲的，有技术含量的题。会持续更新，断更了记得来催更。

CF1037E

有一个 \(n\) 个点 \(m\) 条边的图，每次删掉一条边，然后问你最多能选出多少个点，使得这些点的 导出子图 中每个点度数都 \(\ge k\)。

如果一个点度数 \(< k\)，它显然可以被删除：它不可能再变得 \(\ge k\) 了。然后用类似拓扑排序的思路：先把度数 \(<k\) 的加入队列，每次找队首的点，删掉它，更新周围点的度数；发现周围点有变得 \(<k\) 的，也加入队列。

每次删边就把两个有关点的度数更新。如果 \(<k\) ，就加入队列，跑一遍。

由于每个点只会被删除一次，所以，所有的删边操作加一块的复杂度也是 \(O(n)\) 的。

代码

CF1366E

在 trick - 反向操作日神仙 中

CF1327F

在 trick - 拆位 中

CF1437D

有一颗树，将每个点的所有儿子按编号从小到大排序，依次遍历，得到一个BFS序。现在给你这个BFS序，最小化树的深度。

很simple的贪心，每次找到一段最长的连续的上升的段，然后把它接到当前点的儿子即可。“根据题意模拟”。

代码

CF1413D

有一个序列初始为空，现在有 \(2n\) 个操作，每个操作为：加入某个数（不知道），或者取出指定的数。取出的数就不会放回去，并且必须存在并且是当前最小的数，否则就不满足条件。保证加入和取出各 \(n\) 次。试确定一个满足条件的加入数的方案，或者输出无解。

反向考虑，取数变加数，加数变取数，然后就可以直接确定了。确定的过程中判断一下是否有解即可。

代码

CF1421D

给一个被六边形覆盖的平面，并给每个点一个坐标，像 这样。然后现在起点是 \((0,0)\)，给你向六个方向走的代价（都是正的），求到 \((x,y)\) 的最短路。

假设是平面直角坐标系会不会做？显然会吧，路径显然是（至多）两根线，枚举两个方向，冲就完了。

为什么路径至多两根线呢？因为考虑一个拐弯，我们可以把拐回来的路径省去不走，像这样：

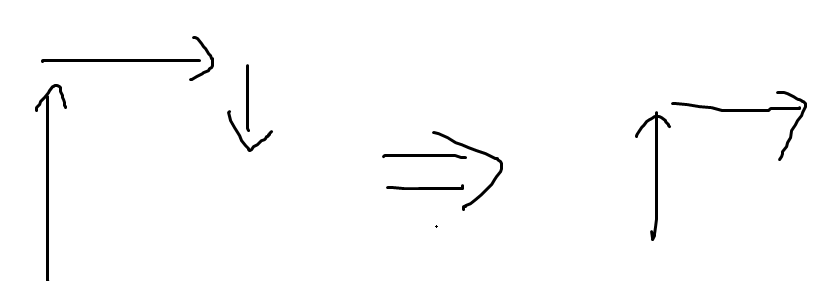
发现这个性质在六边形上也有，所以我们就枚举两个方向，exgcd 判断一下能否能走到，然后用这个代价更新答案就行了。复杂度 \(O(36\times \log V)\)，\(V\) 表示坐标的范围。

代码

CF1423J

数多项式 \(f\)：每一项系数都是 \([0,7]\) 间的整数，且 \(f(2)=m\)。多组询问，\(t\le 5e5\)。

\([0,7]\) 正好八个数，八是 \(2^3\)。考虑三个三个拆开，设系数为 \(c\)：

\((c_0+8c_3+64c_6\cdots)+(2c_1+16c_4+128c_7\cdots)+(4c_2+32c_5+256c_8\cdots )\)

\(=(c_0+8c_3+64c_6\cdots)+2(c_1+8c_4+64c_7\cdots)+4(c_2+8c_5+64c_8\cdots )\)

其中 \(c\) 中的每个数都是 \([0,7]\) 之间，然后我们可以把三个括号里的每一个式子，和一个自然数一一对应起来（写成八进制）。然后就是：\(X+2Y+4Z=m\)

\(x+2y=m\) 有 \(m/2+1\) 个自然数解。然后枚举 \(Z\)，求一下和：

\(\sum\limits_{Z=0}^{m/4} (m-4Z)/2+1=\sum\limits_{Z=0}^{m/4} m/2+1-2Z\)

设 \(S(n)\) 表示 \(1\) 加到 \(n\) 的自然数和。

\(=(m/2+1)\times (m/4+1) - 2S(m/4)\)

然后就可以 \(O(1)\) 算了。还需要代码吗？