Codeforces Round #649 (Div. 2) C、Ehab and Prefix MEXs D、Ehab's Last Corollary 找环和点染色

题目链接：C、Ehab and Prefix MEXs

题意;

有长度为n的数组a(下标从1开始),要求构造一个相同长度的数组b,使得b1,b2,....bi集合中没有出现过的最小的数是ai.

mex函数表示不在集合中的那个最小的自然数

例如：

mex(1,2,3)=0

mex(0,1,2)=3

mex(0,1,3)=2

对于题意你要保证

mex(b1)=a1

mex(b1,b2)=a2

mex(b1,b2,b3)=a3

题解：

首先这个题目肯定是有解的，无解的情况题目都给排除了。

给b数组初始值为n+1，对于ai的值，我们必须保证0——(ai-1) （这代表区间【0，(ai-1)】）这些值都在b1——bi（这代表b1,b2...bi）出现过了。那么我们取b1——bi 中最小的不是n+1的值为x（如果全是n+1，那么x=0），我们从bi向b1逆向枚举，每遇到一个n+1，那就给它赋值x，然后让x++。这样一直操作就没了

至于为什么要逆向操作，这是个贪心，因为小的值ai只会在前面出现（题目要求了ai<=a(i+1)），如果你把小的值放在前面会影响前面答案的正确性

代码：

 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<string>
 5 #include<queue>
 6 #include<string.h>
 7 #include<map>
 8 #include <iostream>
 9 #include <math.h>
10 using namespace std;
11 typedef long long ll;
12 const int maxn=1e5+10;
13 int v[maxn],w[maxn];
14 int main()
15 {
16
17     int n;
18     scanf("%d",&n);
19     for(int i=1; i<=n; ++i)
20     {
21         scanf("%d",&v[i]);
22         w[i]=n+1;
23     }
24     int k=0;
25     for(int i=1; i<=n; ++i)
26     {
27         for(int j=i; j>=1; --j)
28         {
29             if(k>=v[i]) break;
30             if(w[j]==n+1)
31             {
32                 w[j]=k++;
33             }
34         }
35     }
36     for(int i=1; i<=n; ++i)
37     {
38         if(i==n)
39             printf("%d\n",w[n]);
40         else printf("%d ",w[i]);
41     }
42
43     return 0;
44 }

题目链接：D、Ehab's Last Corollary  参考链接：https://www.cnblogs.com/Last--Whisper/p/13143897.html#

题意：

给出一张 nn 个点的无向连通图和一个常数 kk。你需要解决以下任何一个问题中的一个:

• 找出一个大小为⌈k/2⌉的独立集。
• 找出一个大小不超过k的环。

一条边的长度算作1

独立集: 独立集是一个点的集合，满足其中任意两点之间在原图上没有边直接相连。

题解：

这道题也是肯定是有解的，如果它没有环，那么k/2个点的独立集肯定能找到

如果有环，环的长度小于k直接输出，如果大于k，因为它是最小的环，那么任意一个点只会与环中两个点相连才一起构成一个环。那么这个环绝对能找出来k/2个点独立集

我们可以先假设这个图没有环，那只需要随便找一个点开始染色。然后给与这个点相连的其他点染成另外一种颜色。这样不停的染色直到这个图的每一个点都被染色就可以了

如果后面我们确定了就是没有环，那就输出相同颜色的点就可以了

对于确定是否含有环，我们可以事先定义一个vector容器p用它来装已经dfs遍历过的点，并且如果一个点在这个p容器中那就把这个点在数组is_circle中标记一下。如果一个图里面包含环的话，如下图

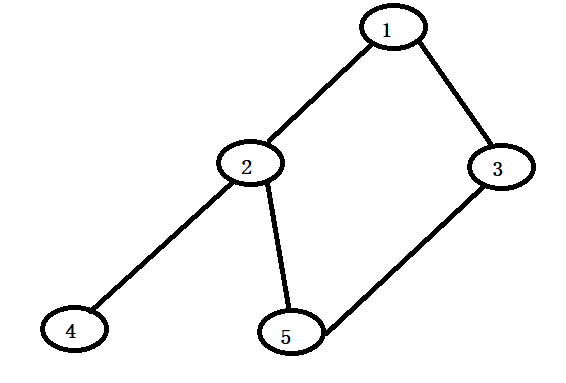
我们从1点开始进行dfs，我们可以看到1，2，3，5构成了一个环。我们进行模拟dfs，从1我们会dfs到2，然后从2我们dfs到5，从5我们dfs到3，从3我们dfs到1我们发现1这个点已经被标记过了。那就证明存在环

如果我们发现了环我们不管这个环是不是最小环（例如，如果多一条边2——3，那么1，2，3，5里面就包含一个小环1，2，3），直接让我们遇到那个标记过的点1到我们dfs到现在遇到的所有点都装入一个容器（也就是把1，2，5，3装入另一个容器）

我们这里说一下height数组，这个数组表示的是某一个点是第几深度遍历到的，对于序列1，2，5，3。height[1]=0,height[2]=1,height[5]=2，height[3]=3;

然后枚举每一条边，如果某条边的两个节点x和y的深度不一样且这两个点都在环中，那就证明这个环不是最小环(假设2——3这条边存在)，那么x和y就是2和3，那就从这个1，2，3，5的开头和结尾删除节点，直到遇见x或者y就截至

代码：

  1 #include<stdio.h>
  2 #include<algorithm>
  3 #include<iostream>
  4 #include<string>
  5 #include<queue>
  6 #include<deque>
  7 #include<string.h>
  8 #include<map>
  9 #include <iostream>
 10 #include <math.h>
 11 using namespace std;
 12 typedef long long ll;
 13 const int maxn=2e5+10;
 14 struct shudui
 15 {
 16     int x,y;
 17 } edge[maxn];
 18 int n,m,k,height[maxn],is_circle[maxn];
 19 vector<int> w[maxn],p,colour[2];
 20 deque<int> circle;
 21 void dfs(int x,int fa)
 22 {
 23     height[x]=p.size();
 24     p.push_back(x);
 25     colour[p.size()%2].push_back(x);
 26     for(int i=0; i<w[x].size(); ++i)
 27     {
 28         int to=w[x][i];
 29         if(to==fa) continue;
 30         if(height[to]==-1)
 31         {
 32             dfs(to,x);
 33         }
 34         else
 35         {
 36             if(circle.empty())
 37             {
 38                 for(int i=height[to]; i<=height[x]; ++i)
 39                 {
 40                     circle.push_back(p[i]);
 41                     is_circle[p[i]]=1;
 42                 }
 43             }
 44         }
 45     }
 46     p.pop_back();
 47 }
 48 int main()
 49 {
 50     memset(height,-1,sizeof(height));
 51     scanf("%d%d%d",&n,&m,&k);
 52     for(int i=0; i<m; ++i)
 53     {
 54         int x,y;
 55         scanf("%d%d",&x,&y);
 56         edge[i].x=x;
 57         edge[i].y=y;
 58         w[x].push_back(y);
 59         w[y].push_back(x);
 60     }
 61     dfs(1,0);
 62     if(circle.empty())
 63     {
 64         printf("1\n");
 65         if(colour[0].size()<colour[1].size()) swap(colour[0],colour[1]);
 66         for(int i=0; i<(k+1)/2; ++i)
 67         {
 68             if(i==0) printf("%d",colour[0][i]);
 69             else printf(" %d",colour[0][i]);
 70         }
 71         printf("\n");
 72         return 0;
 73     }
 74
 75     for(int i=0; i<m; ++i)
 76     {
 77         int x=edge[i].x;
 78         int y=edge[i].y;
 79         if(is_circle[x] && is_circle[y] && abs(height[x]-height[y])>1)
 80         {
 81             while (circle.front() != x && circle.front() != y)
 82             {
 83                 is_circle[circle.front()] = false;
 84                 circle.pop_front();
 85             }
 86             while (circle.back() != x && circle.back() != y)
 87             {
 88                 is_circle[circle.back()] = false;
 89                 circle.pop_back();
 90             }
 91         }
 92     }
 93
 94     if(circle.size()<=k)
 95     {
 96         printf("2\n%d\n",circle.size());
 97         for(int i=0;i<circle.size();++i)
 98         {
 99             if(i==0) printf("%d",circle[i]);
100             else printf(" %d",circle[i]);
101         }
102         printf("\n");
103     }
104     else
105     {
106         printf("1\n");
107         int sum=0;
108         for(int i=0;i<circle.size();i+=2)
109         {
110             if(i==0) printf("%d",circle[i]);
111             else printf(" %d",circle[i]);
112             sum++;
113             if(sum>=(k+1)/2) break;
114         }
115         printf("\n");
116     }
117     return 0;
118 }