GYM101810 ACM International Collegiate Programming Contest, Amman Collegiate Programming Contest (2018) M. Greedy Pirate (LCA)

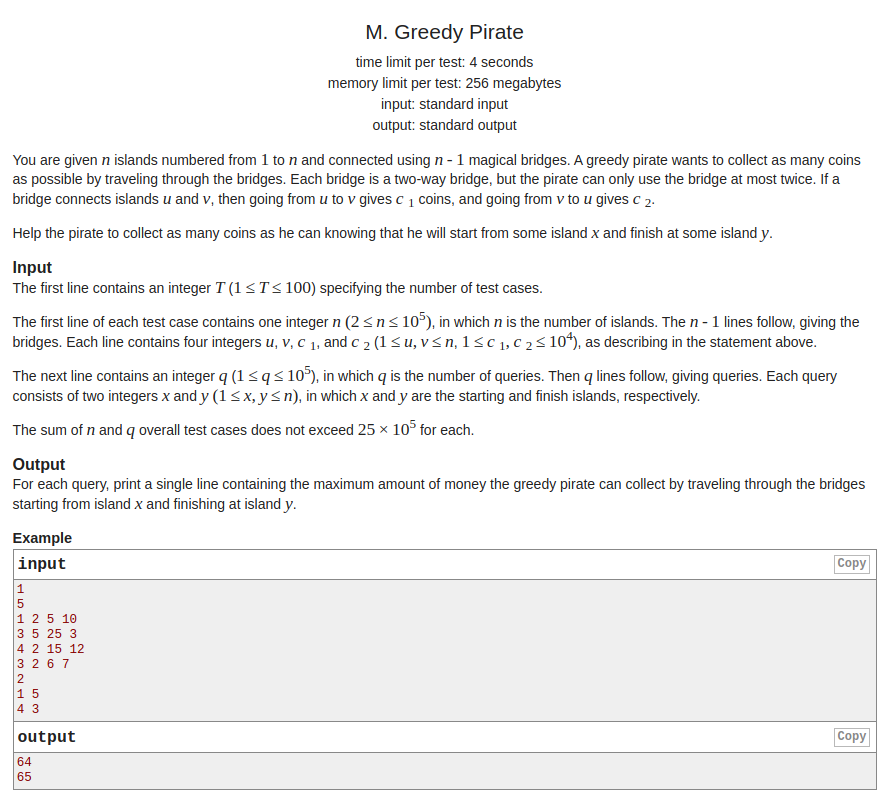
• 题意:有\(n\)个点,\(n-1\)条边,每条边正向和反向有两个权值,且每条边最多只能走两次,有\(m\)次询问,问你从\(u\)走到\(v\)的最大权值是多少.

• 题解:可以先在纸上画一画,不难发现,除了从\(u\)走到\(v\)的路径上的反向权值我们取不到,其他所有边的正反权值均能取到,所以答案就是:\(sum-u->v路径的反向权值\),问题也就转换成了求\(v->u\)的权值,那么这里我们就可以用LCA来求了.

  首先,令一个点为根节点,然后求出\(v\)到根节点的距离和根节点到\(u\)的距离,再减去根节点到\(LCA(u,v)\)的正反权值,就是\(v->u\)的权值.

  这题会卡读入,记得用scanf.

• 代码:

  struct misaka{
  	int out;
  	int val1,val2;
  }p;
  
  int t;
  int n,m;
  int sum;
  vector<misaka> V[N];
  int fa[N][30];
  int depth[N];
  int lg[N];
  int dis1[N],dis2[N];
  bool st[N];
  
  void dfs(int node){            //求每个节点到根节点的距离.
  	st[node]=true;
  	for(auto w:V[node]){
  		int now=w.out;
  		int val1=w.val1;
  		int val2=w.val2;
  		if(st[now]) continue;
  		dis1[now]=dis1[node]+val1;
  		dis2[now]=dis2[node]+val2;
  		dfs(now);
  	}
  }
  
  void presol(int node,int fath){
  	fa[node][0]=fath;
  	depth[node]=depth[fath]+1;
  	for(int i=1;i<=lg[depth[node]]-1;++i){
  		fa[node][i]=fa[fa[node][i-1]][i-1];
  	}
  	for(auto w:V[node]){
  		if(w.out!=node){
  			presol(w.out,node);
  		}
  	}
  }
  
  int LCA(int x,int y){
  	if(depth[x]<depth[y]){
  		swap(x,y);
  	}
  	while(depth[x]>depth[y]){
  		x=fa[x][lg[depth[x]-depth[y]]-1];
  	}
  	if(x==y) return x;
  	for(int k=lg[depth[x]]=1;k>=0;--k){
  		if(fa[x][k]!=fa[y][k]){
  			x=fa[x][k];
  			y=fa[y][k];
  		}
  	}
  	return fa[x][0];
  }
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
  	cin>>t;
  	 while(t--){
  	 	cin>>n;
  	 	sum=0;
  	 	for(int i=1;i<=n-1;++i){
  	 		int u,v,val1,val2;
  	 		cin>>u>>v>>val1>>val2;
  	 		p.out=v,p.val1=val1,p.val2=p.val2;
  	 		V[u].pb(p);
  	 		p.out=u,p.val1=val2,p.val2=p.val1;
  	 		V[v].pb(p);
  	 	}
  
  		for(int i=1;i<=n;++i){
  			lg[i]=lg[i-1]+(1<<lg[i-1]==i);
  		}	 	
  
  		dfs(1);
  		presol(1,0);
  
  		cin>>m;
  		for(int i=1;i<=m;++i){
  			int u,v;
  			cin>>u>>v;
  			cout<<sum-(dis1[u]+dis2[v]-dis1[LCA(u,v)]-dis2[LCA(u,v)])<<endl;
  		}
  
  	 }
  
      return 0;
  }