POJ - 1654 利用叉积求三角形面积 去 间接求多边形面积

题意：在一个平面直角坐标系，一个点总是从原点出发，但是每次移动只能移动8个方向的中的一个并且每次移动距离
只有1和√2这两种情况，最后一定会回到原点（以字母5结束），请你计算这个点所画出图形的面积

题解：

叉积又叫向量积，如下图

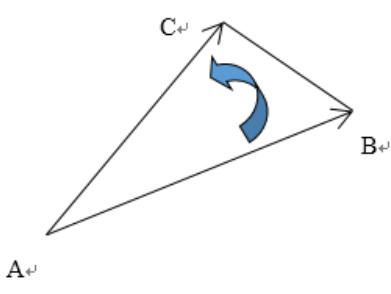
设AC这条边为向量a，AB这条边为向量b，夹角为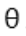

那么会有：

那么一个多边形肯定是可以分解成多个三角形的，把它们的面积加到一起就行了

我们知道三角形的角度不是那么容易就可以求出来的，而且通过向量坐标也可以求向量积的模（下面给出三维模式下的）

二位模式下：

向量a=（x1,y1）,向量b=（x2,y2）

（向量a*向量b）的模=x1*y2-x2*y1

代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<iostream>
 4 #include<algorithm>
 5 #include<math.h>
 6 #include<vector>
 7 #include<queue>
 8 #include<stack>
 9 #include<map>
10 using namespace std;
11 typedef long long ll;
12 const int maxn=1e6+10;
13 const int INF=0x3f3f3f3f;
14 const double eps=1e-8;
15 const double PI=3.1415926;
16 const int mod = 1e9+7;
17 #define mt(A,B) memset(A,B,sizeof(A))
18 #define lson l,m,rt*2
19 #define rson m+1,r,rt*2+1
20 #define SIS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
21 #define zero(x) (((x)>0?(x):-(x))<eps)
22 int dir[8][2]={{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,1},{1,-1},{-1,-1}};//8个方向
23 char str[maxn];
24 int main()
25 {
26     int T;
27     int n,m,i,j;
28     int x,y,u,v;
29     long long A;
30     cin>>T;
31     while(T--)
32     {
33         cin>>str;
34         n=strlen(str);
35         x=0;
36         y=0;
37         A=0;
38         for(i=0;i<(n-1);i++)
39         {
40             if(str[i]=='8')
41             {
42                 u=x+dir[0][0];
43                 v=y+dir[0][1];
44             }
45             else if(str[i]=='2')
46             {
47                 u=x+dir[1][0];
48                 v=y+dir[1][1];
49             }
50             else if(str[i]=='6')
51             {
52                 u=x+dir[2][0];
53                 v=y+dir[2][1];
54             }
55             else if(str[i]=='4')
56             {
57                 u=x+dir[3][0];
58                 v=y+dir[3][1];
59             }
60             else if(str[i]=='9')
61             {
62                 u=x+dir[4][0];
63                 v=y+dir[4][1];
64             }
65             else if(str[i]=='7')
66             {
67                 u=x+dir[5][0];
68                 v=y+dir[5][1];
69             }
70             else if(str[i]=='3')
71             {
72                 u=x+dir[6][0];
73                 v=y+dir[6][1];
74             }
75             else if(str[i]=='1')
76             {
77                 u=x+dir[7][0];
78                 v=y+dir[7][1];
79             }
80             A+=(u*y)-(v*x);//（u,v）,（x,y）和（0,0）原点的叉积算出三角形的面积
81             x=u;
82             y=v;
83         }
84         if(A<0)//顺时针计算是负值
85             A=-A;
86         if(A%2==0)//如果面积可以整除2那么不会有精度缺失
87             cout<<A/2<<endl;
88         else//否则要加上0.5
89             cout<<A/2<<".5"<<endl;
90     }
91     return 0;
92 }