图的广度优先遍历算法（BFS）

在上一篇文章我们用java演示了图的数据结构以及图涉及到的深度优先遍历算法，本篇文章将继续演示图的广度优先遍历算法。广度优先遍历算法主要是采用了分层的思想进行数据搜索。其中也需要使用另外一种数据结构队列，本篇文章为了使代码更加优雅，所有使用java中Linkedlist集合来进行模拟队列。因为该集合有在队列尾部添加元素和从队头取出元素的API。

算法思想：

1.先访问一个元素，然后放到队列中，并且标记已经访问过该元素。

2.然后判断队列是否为空，不为空则取出队头元素。

3.然后取出队头元素的第一个邻接节点并判断该元素是否存在。

4.如果存在再次判断该元素有没有被访问过。

5.如果没有访问过则标记为访问过。同时放到队列中。

6.如果访问过则以头节点为前驱节点，第一个邻接节点为第二个参数查找队头节点的下面的邻接节点

代码以下图为参考：

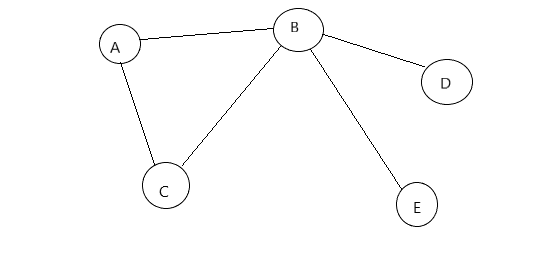
代码如下：

  1 import java.util.ArrayList;
  2 import java.util.Arrays;
  3 import java.util.LinkedList;
  4
  5
  6 public class Graph {
  7
  8     //创建一个集合用来存放顶点
  9     private ArrayList<String> arrayList;
 10     //创建一个二位数组来作为邻接矩阵
 11     private int[][] TwoArray;
 12     //边的数目
 13     private int numOfEdges;
 14     //使用一个数组记录节点是否被访问过
 15     private boolean[] isVisted;
 16     public static void main(String[] args) {
 17         Graph graph = new Graph(5);
 18         //测试
 19         String[] ver={"A","B","C","D","E"};
 20         //将节点放到集合中
 21         for (String s : ver) {
 22          graph.InsertVex(s);
 23         }
 24         //设置边
 25         //A-B A-C B-C B-D B-E
 26         graph.InsertEdeges(0,1,1);
 27         graph.InsertEdeges(0,2,1);
 28         graph.InsertEdeges(1,2,1);
 29         graph.InsertEdeges(1,3,1);
 30         graph.InsertEdeges(1,4,1);
 31         //显示
 32         graph.Show();
 33         graph.BFS();
 34     }
 35
 36     //初始化数据
 37     public Graph(int n){
 38         arrayList=new ArrayList<>(n);
 39         TwoArray=new int[n][n];
 40         numOfEdges=0;
 41         isVisted=new boolean[n];
 42     }
 43
 44     /**
 45      * 根据节点的下标返回第一个邻接节点的下标
 46      * @param index 节点的下标
 47      * @return
 48      */
 49     public int getFirstVex(int index){
 50         for (int i = 0; i < arrayList.size(); i++) {
 51             if(TwoArray[index][i]!=0){
 52                 return i;
 53             }
 54         }
 55         return -1;
 56     }
 57
 58     /**
 59      * 根据前一个节点下标获取下一个节点的下标
 60      * @param v1 找到的第一个节点的
 61      * @param v2 找到的第一个邻接节点并且被访问过的
 62      * @return
 63      */
 64     public int getNextVex(int v1,int v2){
 65         for (int i = v2+1; i < numEdges(); i++) {
 66             if(TwoArray[v1][i]!=0){
 67                 return i;
 68             }
 69         }
 70         return -1;
 71     }
 72
 73     /**
 74      * 广度优先遍历
 75      * @param isVisted 记录是否被访问过的数组
 76      * @param i 想要访问的节点下标
 77      */
 78     public void BFS(boolean[] isVisted,int i){
 79        //表示队列头节点的下标
 80         int u;
 81         //用于存放队列头节点的第一个邻接节点
 82         int w;
 83         //定义一个队列用来存放节点
 84         LinkedList<Object> queue = new LinkedList<>();
 85         //访问该节点
 86         System.out.print(getValue(i)+"->");
 87         //在数组中标记为该下标已经被访问过了
 88         isVisted[i]=true;
 89         //把访问过的节点下标放到队列中，放到队列的尾部
 90         queue.addLast(i);
 91         //判断队列是否为空
 92         while (!queue.isEmpty()){
 93             //队列不为空，那么取出队列的头节点的下标
 94             u=(Integer) queue.removeFirst();
 95             //获取头节点的第一个邻接节点的下标
 96             w = getFirstVex(u);
 97             //判断该节点是否存在
 98             while (w!=-1){
 99                 //说明存在，在判断是否被访问过
100                 if(!isVisted[w]){
101                     //没有访问过，标记为已访问
102                     isVisted[w]=true;
103                     //输出
104                     System.out.print(getValue(w)+"->");
105                     //访问完加入队列中
106                     queue.addLast(w);
107                 }
108                 //以u作为前驱节点，w作为u刚刚访问过的节点，来查找w的下一个邻接节点
109                 w = getNextVex(u, w);
110             }
111         }
112     }
113
114     public void BFS(){
115         for (int i = 0; i < arrayList.size(); i++) {
116             if(!isVisted[i]){
117                 BFS(isVisted,i);
118             }
119         }
120     }
121
122     /**
123      * 添加节点
124      * @param vex
125      */
126     public void InsertVex(String vex){
127         arrayList.add(vex);
128     }
129
130     /**
131      * 设置边
132      * @param v1 第一个节点对应的下标
133      * @param v2  第二节点对应的下标
134      * @param weight 两个节点对应的权值
135      */
136     public void InsertEdeges(int v1,int v2,int weight){
137         TwoArray[v1][v2]=weight;
138         TwoArray[v2][v1]=weight;
139         numOfEdges++;
140     }
141
142     /**
143      * 返回节点对应的个数
144      * @return
145      */
146     public int numVex(){
147         return arrayList.size();
148     }
149
150     /**
151      * 返回边的总个数
152      * @return
153      */
154     public int numEdges(){
155         return numOfEdges;
156     }
157
158     /**
159      * 显示邻接矩阵（图的展示）
160      */
161     public void Show(){
162         for (int[] ints : TwoArray) {
163             System.out.println(Arrays.toString(ints));
164         }
165     }
166
167     /**
168      * 根据下标获取对应的数据
169      * @param i 下标
170      * @return
171      */
172     public String getValue(int i){
173         return arrayList.get(i);
174     }
175
176     public int getWeight(int v1,int v2){
177         int weight=TwoArray[v1][v2];
178         return weight;
179     }
180 }