【AtCoder Beginner Contest 181】A~F题解

越学越菜系列

于2020.11.2,我绿了（错乱）

A - Heavy Rotation

签到题，奇数Black，偶数White。

code:

#include<bits/stdc++.h>
#define N 10000005
#define LL long long
using namespace std;

int t;
int a,b;

inline LL qr()
{
	LL x=0,w=1;char a=0;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

int main()
{
	t=qr();
	if(t%2==1)
	      cout<<"Black"<<endl;
	else
	      cout<<"White"<<endl;
	return 0;
}

B - Trapezoid Sum

依旧是签到题，对于输入每一对数(a,b)求以a为首项，公差为1的等差数列和即可。

code:

#include<bits/stdc++.h>
#define N 1000005
#define LL long long
using namespace std;

int n;
LL a[N],b[N];

inline LL qr()
{
	LL x=0,w=1;char a=0;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

LL ans;

int main()
{
	n=qr();
	for(register int i=1;i<=n;i++)
		a[i]=qr(),b[i]=qr();
	for(register int i=1;i<=n;i++)
		ans+=(b[i]+a[i])*(b[i]-a[i]+1)/2;
	cout<<ans<<endl;
	return 0;
}

C - Collinearity

给你N∈[3,100]个点，判断其中是否有三个点在同一条直线上。

做法：

暴力枚举所有三元组(i,j,k)，根据初中知识，先计算出i,j所在直线的表达式在把k的x轴坐标

代入表达式判断k的y轴坐标与计算结果是否相同即可，注意考虑斜率不存在的情况。

code:

#include<bits/stdc++.h>
#define N 1000005
#define LL long long
using namespace std;

int n;
int x[122],y[122];

inline LL qr()
{
	LL x=0,w=1;char a=0;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

LL ans;
int flag=0;

int main()
{
	n=qr();
	for(register int i=1;i<=n;i++)
		x[i]=qr(),y[i]=qr();
	for(register int i=1;i<=n;i++)//枚举所有三元组
		for(register int j=1;j<=n;j++)
			for(register int k=1;k<=n;k++)
			{
				if(i==j||k==j||i==k)
					continue;
				if(x[i]==x[j])//考虑斜率不存在
				{
					if(x[j]==x[k])
						flag=1;
					continue;
				}
				if(x[k]==x[j])
				{
					if(x[j]==x[i])
					      flag=1;
					continue;
				}
				if(x[k]==x[i])
				{
					if(x[j]==x[i])
						flag=1;
					continue;
				}
                                //y=kx+b;
				double kl=(double)(y[j]-y[i])/(double)(x[j]-x[i]);//计算斜率，表达式中的k
				double kb=y[i]-x[i]*kl;//表达式中的b
				double ky=(double)x[k]*kl+kb;//将x代入表达式
				double yyy=y[k];
				if(yyy-0.00000001<=ky&&ky<=yyy+0.00000001)//浮点数比较
				{
					//cout<<i<<' '<<j<<' '<<k<<endl;
					flag=1;
					break;
				}
			}
	if(flag)
		cout<<"Yes"<<endl;
	else
		cout<<"No"<<endl;
	return 0;
}

D - Hachi

输入一个字符串，每个字符为1~9中一个数字

判断是否能通过重新排列字符串，使得字符串代表的数字为8的倍数。

做法:

暴力枚举

猜测8的所有倍数满足一定性质（类比3的倍数各项和也为3的倍数）

通过对一定范围内8的倍数打表，结果没找到性质QWQ。

最后通过百度，发现所有8的倍数，满足后三位也为8的倍数（度娘吼啊！）。

那么即可先统计字符串内所有数字的数量，再枚举1~999所有8的倍数，统计这一个数各个位数数字的数量，

与之前统计的字符串内所有数字的数量比较判断即可。

要注意字符串长度≤2的情况，特判一下。

code:

#include<bits/stdc++.h>
#define N 1000005
#define LL long long
using namespace std;

char a[200005];

inline LL qr()
{
	LL x=0,w=1;char a=0;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

LL ans;
int flag=0;
int cnt[111];
int cn[11]={};

int main()
{
	cin>>(a+1);
	int n=strlen(a+1);
	for(register int i=1;i<=n;i++)//统计字符串内所有数字的数量
		cnt[a[i]^48]++;
	for(register int i=1;i*8<1000;i++)
	{
		int op=i*8;//枚举1~999所有8的倍数
		for(register int j=0;j<=9;j++)//清空上一次枚举的情况
			cn[j]=0;
		int c=0;
		while(op)//统计op的位数及所有位数字数量
		{
			c++;
			cn[op%10]++;
			op/=10;
		}
		if(n>3&&c<3)//特判
			continue;
		if(n==2&&c!=2)
			continue;
		if(n==1&&c!=1)
			continue;
		int ko=1;
		for(register int j=0;j<=9;j++)//比较判断
			if(cnt[j]<cn[j])
				ko=0;
		if(ko==1)
		{
			//cout<<i*8<<endl;
			cout<<"Yes"<<endl;
			return 0;
		}
	}
	cout<<"No"<<endl;
	return 0;
}

E - Transformable Teacher

有一个含有n个数的数列a，和一个含有m个数的数列b。在b中选择一个数插入a中，并排列a，使得下面的式子最小。

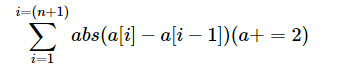
做法:

推论:要使该式子最小，a序列应满足单调性。

可得到以下做法：

将原a数组排序，对于b中每一个数插入到与其值相近的a中计算答案。

时间复杂度为O（nm）。

考虑优化：

• 维护a数组差分前缀和可避免大量重复计算。
• 可以发现在枚举判断a时，a存在单调性，可通过二分查找较快的找到相应位置。
  
  时间复杂度可优化到O((m+n)logn)。
• 也可以先将b数组排序，建立双指针，顺序枚举所有的a数组，当满足b[i]的值与a[i]相邻时，
  
  计算该情况答案，最后统计答案最小值即可。
  
  复杂度O(nlogn+mlogm)。

下面给出该做法的代码(因为我比较懒，代码中可能有部分冗余，见谅):

#include<bits/stdc++.h>
#define N 1000005
#define LL long long
using namespace std;

int n,m;
LL a[200005],b[200005];
LL cha[200005],sum[200004];

inline int qr()
{
	int x=0,w=1;char a=0;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

LL ans=0x3f3f3f3f3f3f3f3f;

int main()
{
	n=qr();
	m=qr();
	for(register int i=1;i<=n;i++)
		a[i]=qr();
	for(register int j=1;j<=m;j++)
		b[j]=qr();
	sort(a+1,a+n+1);
	sort(b+1,b+m+1);//对a,b排序
	for(register int i=2;i<=n;i++)
		cha[i]=a[i]-a[i-1];
	for(register int i=1;i<=n;i++)
		if(i>=2)//sum[i]为以i为结尾，从后往前两两作查的前缀和
			sum[i]=sum[i-2]+cha[i];//维护前缀和，至于为什么是i-2,显然QAQ
	int tot=1;//建立数组b的指针（假的）
	for(register int i=1;i<=n;i++)
	{
		if(tot>m)
			break;
		if(i==1)//特判i==1
			while(b[tot]<=a[i]&&tot<=m)
			{
				ans=min(ans,a[i]-b[tot]+sum[n]-sum[1]);
				tot++;
			}
		if(i==n)//特判i==n
			while(b[tot]>=a[i]&&tot<=m)
			{
				ans=min(ans,sum[i-1]+b[tot]-a[i]);
				tot++;
			}
		while((b[tot]>=a[i]&&b[tot]<=a[i+1])&&tot<=m)
		{
			if(i%2==0)
				ans=min(ans,sum[i]+abs(a[i+1]-b[tot])+sum[n]-sum[i+1]);
			else
				ans=min(ans,sum[i-1]+abs(b[tot]-a[i])+sum[n]-sum[i]);
			tot++;
		}
	}
	cout<<ans<<endl;
	return 0;
}

F - Silver Woods

设y=100，y=-100为平面直角坐标系上下界，在坐标系中有n（1≤n≤100）个钉子，现要使半径为r的气球从坐标系左端移动到右端，并使得气球不超过上下界且不能碰到钉子，求气球的最大半径，精度为(10^(-4))。

做法：

• 首先，考虑二分答案，答案上下界分别为0和100显然。
• 其次，有一个十分巧妙的做法，将每一个钉子看做半径为r的圆，将气球看做点，气球路径上下界分别看做100-r和-100+r。
• 那么，则钉子所代表的圆相交的话则代表“此路不通”，那么如果存在一系列相交的圆横贯上下界，则该r无法成立（妙哇Orz）。

综上：用二分答案的方式枚举可能的r，用并查集维护相交的圆以及集合的最高点和最低点，最后对于每个集合判断即可。

Code:

#include<bits/stdc++.h>
using namespace std;

int n,fa[300];
double dis[300][300];
double l=0.0,r=100.0;
const double inf=0.000000000001;
double x[300],y[300],hig[300],dep[300];

inline int qr()
{
	char a=0;int x=0,w=1;
	while(a<'0'||a>'9'){if(a=='-')w=-1;a=getchar();}
	while(a<='9'&&a>='0'){x=(x<<3)+(x<<1)+(a^48);a=getchar();}
	return x*w;
}

inline int Find(int x)//并查集路径压缩
{
	int t1=x,t2;
	while(fa[t1]!=t1)
		t1=fa[t1];
	while(fa[x]!=x)
	{
		t2=fa[x];
		fa[x]=t1;
		x=t2;
	}
	return x;
}

int main()
{
	n=qr();
	for(register int i=1;i<=n;i++)
		x[i]=qr(),y[i]=qr();
	for(register int i=1;i<=n;i++)
		for(register int j=1;j<=n;j++)
			dis[i][j]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));//预处理出任意两点间距离
	while(l+inf<r)
	{
		double mid=(l+r)/2;
		for(register int i=1;i<=n;i++)
		{
			hig[i]=y[i]+mid;//处理集合中最高点
			dep[i]=y[i]-mid;//处理集合中最低点
			fa[i]=i;//预处理并查集
		}
		int flag=1;
		for(register int i=1;i<=n;i++)//
			for(register int j=1;j<=n;j++)
			{
				if(i==j)
					continue;
				if(dis[i][j]<(mid*2))
				{
					int fi=Find(i);
					int fj=Find(j);
					fa[fj]=fi;//并查集合并
					hig[fi]=max(hig[fi],hig[fj]);//更新并查集最高点
					dep[fi]=min(dep[fi],dep[fj]);//更新并查集最低点
				}
			}
		for(register int i=1;i<=n;i++)//枚举每一个并查集如果有一个集合将道路全部封死则不可通过
			if(fa[i]==i)
				if(hig[i]+mid>100.0000&&dep[i]-mid<-100.0000)
					flag=0;
		if(flag)
			l=mid+inf;
		else
			r=mid;
	}
	printf("%.10f\n",l);
	return 0;
}