jzoj 6798. 【2014广州市选day2】regions

Description

在平面上堆叠着若干矩形，这些矩形的四边与平面X坐标轴或Y坐标轴平行。下图展示了其中一种情况，3个矩形的边将平面划分成8个区域：



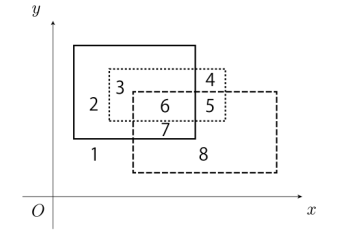
下面展示了另一种稍稍复杂一些的情况：



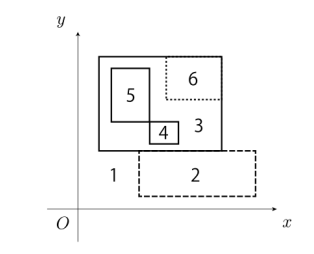
你的任务是写一个程序，判断这些矩形将平面分成了几个区域。

Input

输入的第一行是一个正整数n（n<=50），分别矩形的数目，接下来的n行，每行有4个用空格分隔的整数li,ti,ri,bi（1<=i<=n）代表了第i个矩形的坐标，（li,ti）代表该矩形左上角的X坐标和Y坐标，(ri,bi)代表该矩形右下角的X坐标和Y坐标，0<=li<ri<=\(10^{6}\)，0<=bi<ti<=\(10^{6}\)）

Output

输出只有一个整数，代表这些矩形将平面划分成多少区域。

Solution

这道题有两个做法。

首先先将横坐标纵坐标离散化。

第一个做法：

用并查集，将相连的块连接起来，最后查有多少个块

第二个做法：

将边打上标记，将没被打标记的点进行扩散，统计块数

（作者用的是第一个做法）

Code

#include <cstdio>
#include <algorithm>
#define open(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout);
using namespace std;
int i,p,last,fa[500001],n,j,heng,shu,l,r,ans,u,v,bj[500001];
bool bz[1001][1001];
struct re{
    int x1,x2,y1,y2;
}a[51];
struct node{
    int a,pl;
}k[100001];
const int d[5][2]={{0,0},{-1,0},{1,0},{0,1},{0,-1}};
bool cmp(node x,node y){return x.a<y.a;}
bool rec(node x,node y){return (x.pl<y.pl)||(x.pl==y.pl && x.a<y.a);}
int gf(int x)
{
    if (x==fa[x]) return x;
    fa[x]=gf(fa[x]);
    return fa[x];
}
void ls()
{
    sort(k+1,k+2*n+1,cmp);
    p=0,last=0;
    for (i=1;i<=n+n;i++)
    {
        if (k[i].a==k[i-1].a) k[i-1].a=last;else
        {
            k[i-1].a=last;
            last=++p;
        }
    }
    k[n+n].a=last;
    sort(k+1,k+2*n+1,rec);
}
int main()
{
    open("regions");
    scanf("%d",&n);
    for (i=1;i<=n;i++)
    {
        scanf("%d%d%d%d",&a[i].x1,&a[i].y1,&a[i].x2,&a[i].y2);
        k[i].a=a[i].x1;k[i+n].a=a[i].x2;
        k[i].pl=k[i+n].pl=i;
    }
    ls();
    heng=p*2;
    for (i=1;i<=n;i++)
    {
        a[i].x1=k[2*i-1].a*2;a[i].x2=k[2*i].a*2;
    }
    for (i=1;i<=n;i++)
    {
        k[i].a=a[i].y1;k[i+n].a=a[i].y2;
        k[i].pl=k[i+n].pl=i;
    }
    ls();
    shu=p*2;
    for (i=1;i<=n;i++)
    {
        a[i].y1=k[2*i-1].a*2;a[i].y2=k[2*i].a*2;
    }
    for (i=1;i<=n;i++)
    {
        l=a[i].x1;r=a[i].x2;
        for (j=a[i].y1;j<=a[i].y2;j++)
            bz[l][j]=bz[r][j]=1;
        l=a[i].y1;r=a[i].y2;
        for (j=a[i].x1;j<=a[i].x2;j++)
            bz[j][l]=bz[j][r]=1;
    }
    for (i=0;i<=heng;i++)
    {
        for (j=0;j<=shu;j++)
            fa[i*shu+j]=i*shu+j;
    }
    for (i=0;i<=heng;i++)
    {
        for (j=0;j<=shu;j++)
        {
            if (bz[i][j]) continue;
            for (l=1;l<=4;l++)
            {
                if (i+d[l][0]<=heng && i+d[l][0]>=0 && j+d[l][1]<=shu && j+d[l][1]>=0)
                {
                    if (!bz[i+d[l][0]][j+d[l][1]])
                    {
                        u=gf(i*shu+j);
                        v=gf((i+d[l][0])*shu+j+d[l][1]);
                        if(fa[v]!=u) fa[u]=v;
                    }
                }
            }
        }
    }
    for (i=0;i<=heng;i++)
    {
        for (j=0;j<=shu;j++)
        {
        	if (bz[i][j]) continue;
        	u=gf(i*shu+j);
            if (!i || !j || i==heng || j==shu)
            {
                if (!bj[u])bj[u]=2;
                if (bj[u]==1) bj[u]=2,ans--;
            }
            if (!bj[u])
            {
                bj[u]=1;
                ans++;
            }
        }
    }
    printf("%d",ans+1);
    return 0;
}