[BZOJ 4818/LuoguP3702][SDOI2017] 序列计数 (矩阵加速DP)

题面:

传送门:https://www.lydsy.com/JudgeOnline/problem.php?id=4818

Solution

看到这道题,我们不妨先考虑一下20分怎么搞

想到暴力,本蒟蒻第一反应就是dfs,想法也很简单:

枚举n个数中的每一个数,枚举完每一种情况都判断一下是否满足要求

复杂度O（n^m）

显然,这样的复杂度一分都得不到,但是可以作为对拍用的暴力程序

既然dfs行不通了,那我们换个想法吧,考虑一下用dp来搞这个问题

设 f[i][j] 表示选到第i个数,前i个数的总和%p为j

转移也很好写

我们枚举一下上一个数字是啥就好

f[i][j]= sigma f[i-1][((j-k)%p+p)%p]   k:[1,m]

i:[1,n] j:[0,p-1] 

注意一下: j-k有可能是负数,所以要用负数取模的方法

初始化 f[0][0]=1 (没有数字时,仅有总和为0的情况有一种可行方法)

题目要求的有质数用一个简单的容斥就可以了

我们再做一个没有质数的dp,转移方程跟上面一样,仅需要保证 k 不为质数就行

最后将两者的i为n,j为0的状态相减就是最后答案了.

时间复杂度 O(n*p*m),20分

接下来,我们可以考虑一个很妙的优化

我们发现上面的转移方程

f[i][j]= sigma f[i-1][((j-k)%p+p)%p]   k:[1,m]

i:[1,n] j:[0,p-1]

j是从0~p-1的,而k是从1~m的

这说明了,f[i-1][j]中的某些项是会重复计算到下一个状态的

这样子,我们可以考虑做一个预处理,减少重复计算造成的时间的浪费

考虑这样做:

我们通过一个O(m)的预处理,计算出每一个从0~p-1的数可能从多少个1~m中的数%p计算而得

用一个tot[k]存储下来,tot[k]的意义为:1~m的数%p为k的有多少个

那么这样子,我们的转移方程可优化成这样子

f[i][j]= sigma f[i-1][((j-k)%p+p)%p]*tot[k]   k:[0,p-1]

i:[1,n] j:[0,p-1] 

因为 (j-k)%p = j%p - k%p;

所以说,每一个f[i-1][j%p - k%p]被算的次数仅与有多少个 K1%p=K2%p=K3%p=....有关

我们可以设K1%p=K2%p=K3%p=...=y

原式就可以变为f[i][j]=sigma f[i][j%p-y]*tot[y]

而tot[y]已在前面的预处理解决了

这样,时间复杂度就成功的降为了:O(n*p*p)

然而并没有什么卵用,因为出题者并没有设计这一档的分

我们再考虑一个优化

f[i][j]= sigma f[i-1][((j-k)%p+p)%p]*tot[k]   k:[0,p-1]

i:[1,n] j:[0,p-1] 

原转移式是不是有一个特征?对,那就是式子是固定死的,这意味着我们可以用矩阵优化至O(m^3long n)

这种类型的转移矩阵我称为"一层层"的转移,可以考虑这样列转移矩阵

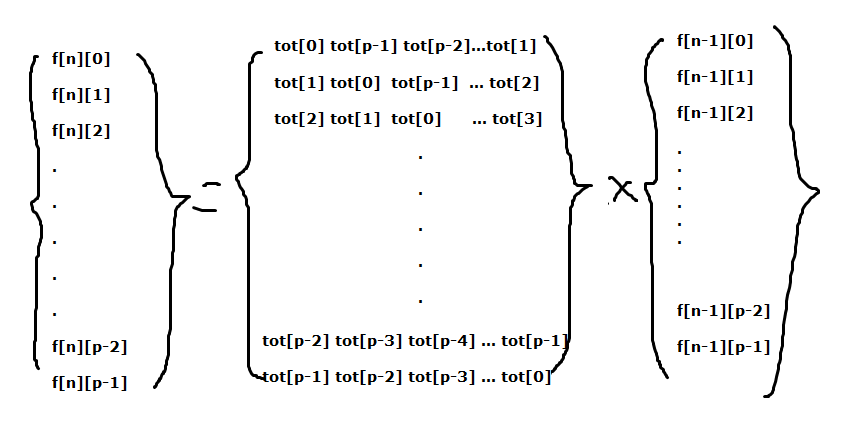
然后就OK啦

Code

//Luogu P3702 [SDOI2017]序列计数
//Apr,11th,2018
//矩阵加速DP
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int P=100+10;
const int M=20000000+100;
const int poi=20170408;
struct MAT
{
    int x,y;
    long long a[P][P];
    MAT (int tx,int ty)
    {
        x=tx,y=ty;
        memset(a,0,sizeof a);
    }
    friend MAT operator * (MAT A,MAT B)
    {
        MAT ans=MAT(B.x,A.y);
        for(int i=1;i<=ans.y;i++)
            for(int j=1;j<=ans.x;j++)
                for(int k=1;k<=A.x;k++)
                {
                    ans.a[i][j]+=A.a[i][k]*B.a[k][j];
                    if(ans.a[i][j]>=poi) ans.a[i][j]%=poi;
                }
        return ans;
    }
};
MAT FastPow(MAT a,int b)
{
    if(b==1) return a;
    MAT ans=FastPow(a,b/2);
    ans=ans*ans;
    if(b%2==1) ans=ans*a;
    return ans;
}
int n,m,p,tot[P];
bool IsPrime[M];
int prime[M],p_tot;
void GetPrime()
{
    memset(IsPrime,1,sizeof IsPrime);
    IsPrime[0]=IsPrime[1]=0;
    for(int i=2;i<=m;i++)
    {
        if(IsPrime[i]==true) prime[++p_tot]=i;
        for(int j=1;j<=p_tot and prime[j]*i<=m;j++)
        {
            IsPrime[prime[j]*i]=false;
            if(i%prime[j]==0) break;
        }
    }
}
int main()
{
    n=read(),m=read(),p=read();

    for(int i=1;i<=m;i++)
        tot[i%p]++;
    GetPrime();
    MAT A=MAT(p,p);
    for(int i=1;i<=p;i++)
        for(int j=1;j<=p;j++)
            A.a[i][j]=tot[((i-j)%p+p)%p];
    MAT B=MAT(1,p);
    for(int i=1;i<=p;i++)
        B.a[i][1]=tot[i-1];
    long long ans=(FastPow(A,n-1)*B).a[1][1];

    memset(tot,0,sizeof tot);
    for(int i=1;i<=m;i++)
        if(IsPrime[i]==false)
            tot[i%p]++;
    for(int i=1;i<=p;i++)
        for(int j=1;j<=p;j++)
            A.a[i][j]=tot[((i-j)%p+p)%p];
    for(int i=1;i<=p;i++)
        B.a[i][1]=tot[i-1];
    ans-=(FastPow(A,n-1)*B).a[1][1];

    printf("%lld",(ans%poi+poi)%poi);
    return 0;
}

C++