题解 洛谷 P5465 【[PKUSC2018]星际穿越】

首先考虑题目的性质，发现点向区间连的边为双向边，所以也就可以从一个点向右跳到区间包含该点的点，如图所示：

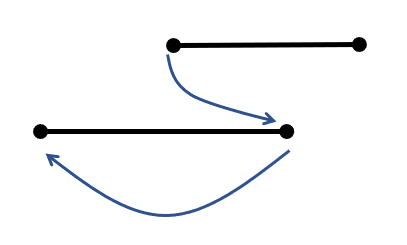
但事实上向后跳其实是不优的，可以有更好的方法来节省花费：

因此我们发现一个点跳到其前一个区间的花费为 \(1\)，且在跳跃过程中不会向右跳，同时我们还证明了一个点向左的花费单调递增。

但是从起点进行第一步跳跃时，有可能会向后跳：

其通过向后跳来到达一个更大的包含该点的区间，然后使下一步跳跃到达一个更向前的位置，第一步采取向后跳方案的花费为 \(2\)。

发现只有第一步是特殊的，所以单独来考虑第一步的情况。

设 \(pos_i=\min\limits_{j=i}^n l_j\)，即 \(l_i\) 的后缀最小值，\(pos_i\) 即为位置 \(i\) 第一步采取向后跳方案来到达的最向前的位置。

对每个位置建可持久化线段树，线段树中对应的值为该位置不考虑第一步的花费，位置 \(i\) 的线段树从位置 \(pos_i\) 转移过来，然后在区间 \([1,i-1]\) 通过标记永久化来实现区间加一，表示不是第一步跳的花费。

查询时只需在 \(l_x\) 所对应的线段树上查询区间 \([l,min(r,l_x-1)]\) 的和，其为位置 \(x\) 除去第一步的总花费，然后再加上第一步花费的贡献即可。

\(code:\)

#include<bits/stdc++.h>
#define maxn 300010
#define maxm 10000010
#define mid ((l+r)>>1)
using namespace std;
typedef long long ll;
template<typename T> inline void read(T &x)
{
    x=0;char c=getchar();bool flag=false;
    while(!isdigit(c)){if(c=='-')flag=true;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    if(flag)x=-x;
}
int n,q,tot;
int a[maxn],pos[maxn],rt[maxn],ls[maxm],rs[maxm];
ll sum[maxm],add[maxm];
ll gcd(ll a,ll b)
{
    return b?gcd(b,a%b):a;
}
void modify(int L,int R,int l,int r,int &cur)
{
    int x=++tot;
    ls[x]=ls[cur],rs[x]=rs[cur],add[x]=add[cur];
    sum[x]=sum[cur]+(min(R,r)-max(L,l)+1),cur=x;
    if(L<=l&&R>=r)
    {
        add[cur]++;
        return;
    }
    if(L<=mid) modify(L,R,l,mid,ls[cur]);
    if(R>mid) modify(L,R,mid+1,r,rs[cur]);
}
ll query(int L,int R,int l,int r,int cur)
{
    if(L>R) return 0;
    if(L<=l&&R>=r) return sum[cur];
    ll v=add[cur]*(min(R,r)-max(L,l)+1);
    if(L<=mid) v+=query(L,R,l,mid,ls[cur]);
    if(R>mid) v+=query(L,R,mid+1,r,rs[cur]);
    return v;
}
int main()
{
    read(n);
    for(int i=2;i<=n;++i) read(a[i]),pos[i]=a[i];
    for(int i=n-1;i>=2;--i) pos[i]=min(pos[i],pos[i+1]);
    for(int i=2;i<=n;++i) rt[i]=rt[pos[i]],modify(1,i-1,1,n,rt[i]);
    read(q);
    while(q--)
    {
        int l,r,x;
        ll g,v;
        read(l),read(r),read(x),v=r-l+1;
        v+=query(l,min(r,a[x]-1),1,n,rt[a[x]]);
        g=gcd(v,r-l+1),printf("%lld/%lld\n",v/g,(r-l+1)/g);
    }
    return 0;
}