7.20试机测 T3 阶乘之和 暴力AC题解
7.20试机测 T3 阶乘之和 暴力AC题解
题外话:此乃本蒟蒻发表的第一篇题解,大家多多关照,支持一下,谢谢
题面
3、阶乘之和(sum.pas/in/out)
问题描述: 给定一个非负整数 n,请你判断 n 是否可以由一些非负整数的阶乘相加得到。
问题输入: 有若干组数据。每行一个整数 n,保证 n<1000000。 以负数结束输入。
问题输出: 对于每组数据输出一行,若可以则输出‘YES’,否则输出‘NO’。
输入样例: 9 -1
样例输出: YES
分析
这个题嘛
大概了解了一下题意,就是给出n,判断n能不能被几个数的阶乘加起来。(虽然题目没有说清楚数字能不能重复,但是我们知道1的阶乘是1,如果数字可以重复的话,那么任何n都是YES了,所以我推测所选数字不能重复)
题目让输入多组数据,我们先针对一个数据进行操作,在结尾再弄关于输入多组数据的问题…………
下面算出一些较小数的阶乘(千万不要忘记0)(这一步可以在Excel完成,用FACT函数)


看到数据范围, n<1000000,可以了解到所选的数字应该在0~9里。
那么,n的最大值就确定了,即0~9的阶乘之和(1+1+2+6+24+...+40320+362880=409114)
也就是说,只要n的值超过了409114,那么这个n就不符合条件,可以提前判断一部分n是不是NO。
还有,0的阶乘是1,那么如果n的值为0,就没有非负整数满足n,也是直接NO。
if(n> || n==)
cout<<"NO"<<endl;
下面怎么办呢,暴力?!
在这里,我还没有学一些什么神奇01背包,二进制什么玩意……
我就简简单单地用几个for循环来搜出所有情况吧。
先开一个数组(第一个开0是防止有??的情况 其实第一个完全可以不开0,不开0还节省了时间)
long long x[]= {,,,,,,,,,,};
我们知道,题目给定一个n,这个n可能由上面数组中的1个数相加得到,也可能是2个,也可能是多个……
(比如n=4时,n是1+1+2,由数组中的3个数相加得到;n=25时,则为1+24,由数组中的2个数相加得到)
那么,我们先假设n由上面选1个数得到,则可以
for(int a=; a<; ++a)
if(x[a]==n)
{
cout<<"YES"<<endl;
}
如果一个数不行,那就看看2个数加起来能不能得到n
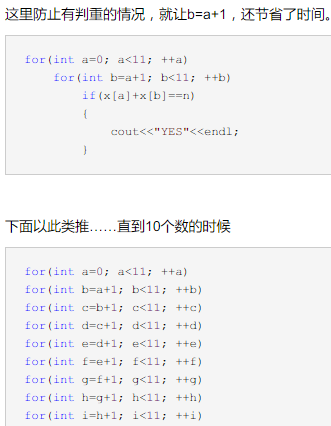
这里防止有判重的情况,就让b=a+1,还节省了时间。
for(int a=; a<; ++a)
for(int b=a+; b<; ++b)
if(x[a]+x[b]==n)
{
cout<<"YES"<<endl;
}
下面以此类推……直到10个数的时候
for(int a=; a<; ++a)
for(int b=a+; b<; ++b)
for(int c=b+; c<; ++c)
for(int d=c+; d<; ++d)
for(int e=d+; e<; ++e)
for(int f=e+; f<; ++f)
for(int g=f+; g<; ++g)
for(int h=g+; h<; ++h)
for(int i=h+; i<; ++i)
for(int j=i+; j<; ++j)
if(x[a]+x[b]+x[c]+x[d]+x[e]+x[f]+x[g]+x[h]+x[i]+x[j]==n)
{
cout<<"YES"<<endl;
}
这样就行了?此处忽略了一个地方,假设n由5个数相加就能得到,那么下面的6次,7次循环再执行岂不是浪费掉了时间嘛。
所以,我们开一个布尔变量,用来判断n是不是已经被配对了
bool yes=false;
好了,现在我们可以研究输入多组数据的问题了,因为不研究这个,布尔变量就没法展现它的作用。
题意说输入负数的时候结束程序(千万不要被样例迷惑了,不一定是-1结束程序)
那么,可以用while循环输入数据。
每输入一个n,就对n执行一次下面的操作。 直到n<0时,return 0 结束程序。
<0
int main()
{
while(scanf("%d",n) && n>=)
{
yes=false;
//此处往下写程序,每次当n配对时,把布尔变量变成true。
}
return 0;
}
当n被配对时,变量yes的值为true。我们可以在程序中疯狂检测 yes的值,只要是true就立即让它输出“YES”,然后扔掉此时的n,再对下一个数字n进行操作。
具体操作如下(拿n由4个数相加得到 举例):
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
if(x[a]+x[b]+x[c]+x[d]==n)
{
cout<<"YES"<<endl;
yes=true; //只要n被配对成功,就把布尔设为true
break;
}
if(yes==true) break; //让被配对成功的n 一路顺风,跳出循环
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue; //此时的 continue 与 while 读入操作在同一层。这样就可以读入下一个n了
这样看起来好像有点麻烦,但是我觉得理解起来不难吧qwq.
最后当10次循环都走一遍,结果n没有找到合适的数字,就在末尾输出“NO”.
AC代码:
/*---------------------------------
*Title number: 7.20 试机测 T3 阶乘之和
*Creation date: 2020-07-20 afternoon
*By: EdisonBa
*-------------------------------*/
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std; long long x[]= {,,,,,,,,,,};
long long n;
bool yes=false; int main()
{
while(cin>>n && n>=)
{
yes=false; //每一次对n操作都要重置一下布尔变量 yes
//下面判一下最大值和0
if(n> || n==)
{
cout<<"NO"<<endl;
continue;
}
//下面进行第 1 次循环
for(int a=; a<; ++a)
if(x[a]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
} if(yes==true) continue;
//下面进行第 2 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b) if(x[a]+x[b]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 3 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c) if(x[a]+x[b]+x[c]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 4 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
if(x[a]+x[b]+x[c]+x[d]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 5 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
{
for(int e=d+; e<; ++e)
if(x[a]+x[b]+x[c]+x[d]+x[e]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 6 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
{
for(int e=d+; e<; ++e)
{
for(int f=e+; f<; ++f)
if(x[a]+x[b]+x[c]+x[d]+x[e]+x[f]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 7 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
{
for(int e=d+; e<; ++e)
{
for(int f=e+; f<; ++f)
{
for(int g=f+; g<; ++g)
if(x[a]+x[b]+x[c]+x[d]+x[e]+x[f]+x[g]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 8 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
{
for(int e=d+; e<; ++e)
{
for(int f=e+; f<; ++f)
{
for(int g=f+; g<; ++g)
{
for(int h=g+; h<; ++h)
if(x[a]+x[b]+x[c]+x[d]+x[e]+x[f]+x[g]+x[h]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 9 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
{
for(int e=d+; e<; ++e)
{
for(int f=e+; f<; ++f)
{
for(int g=f+; g<; ++g)
{
for(int h=g+; h<; ++h)
{
for(int i=h+; i<; ++i) if(x[a]+x[b]+x[c]+x[d]+x[e]+x[f]+x[g]+x[h]+x[i]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
//下面进行第 10 次循环
for(int a=; a<; ++a)
{
for(int b=a+; b<; ++b)
{
for(int c=b+; c<; ++c)
{
for(int d=c+; d<; ++d)
{
for(int e=d+; e<; ++e)
{
for(int f=e+; f<; ++f)
{
for(int g=f+; g<; ++g)
{
for(int h=g+; h<; ++h)
{
for(int i=h+; i<; ++i)
{
for(int j=i+; j<; ++j)
if(x[a]+x[b]+x[c]+x[d]+x[e]+x[f]+x[g]+x[h]+x[i]+x[j]==n)
{
cout<<"YES"<<endl;
yes=true;
break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
}
if(yes==true) break;
} if(yes==true) continue;
// 10次循环完毕,若n没有合适的数字,输出"NO" cout<<"NO"<<endl; } return ;
}
https://www.luogu.com.cn/record/35414283
(此代码对于 第10个毒瘤点来说 能过就是奇迹)
这份代码,显然不是最优解(第10个测试点的时间快要爆了),如果把x数组里的0删去,可能时间会稍微短那么几毫秒。
但是这个理解起来很容易,只要有充足的时间就能写出来(大概半个多小时)。
我觉得这个代码的关键就是在每次大循环中,下层的for的变量值是上层的变量值+1(无法表述啊这)
-----------------------------------------------------------------------------------------------------------------------------------------------
看图:
-----------------------------------------------------------------------------------------------------------------------------------------------
这样节省了大部分时间,也防止出现了判重的情况,使得多次大循环顺利过测试点。
感谢您观看此题解。
这是本蒟蒻发表的第一篇题解,岂不妙哉?!
希望在接下来的时间里,大家共同成长,共同进步,多多交流,共创辉煌!
EdisonBa
2020/7/20
7.20试机测 T3 阶乘之和 暴力AC题解的更多相关文章
- HPU 第三次积分赛:阶乘之和(水题)
阶乘之和 描述 对于整数pp,给出以下定义 p=x_{1}!+x_{2}!+x_{3}!+...+x_{q}!(x_{i}<x_{j}for\ all\ i<j )p=x1!+x2!+ ...
- nyoj阶乘之和
/*阶乘之和 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描写叙述 给你一个非负数整数n,推断n是不是一些数(这些数不同意反复使用,且为正数)的阶乘之和, 如9=1! ...
- PTA 阶乘之和取模
阶乘之和取模 (25 分) 输入正整数n, 计算S = 1!+2!+...+n!的末6位(不含前导0). 这里1<=n<=109. 输入样例: 例如输入: 20 输出样例: 输出: ...
- 7-49 求前n项的阶乘之和 (15 分)
从键盘输入一个整数n,求前n项的阶乘之和,1+2!+3!+...+n!的和 输入格式: 输入一个大于1的整数.例如:输入20. 输出格式: 输出一个整数.例如:2561327494111820313. ...
- Java实现 洛谷 P1009 阶乘之和
import java.util.Scanner; public class 阶乘之和 { public static void main(String[] args) { Scanner sc = ...
- nyoj 91 阶乘之和(贪心)
阶乘之和 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描述 给你一个非负数整数n,判断n是不是一些数(这些数不允许重复使用,且为正数)的阶乘之和,如9=1!+2!+3! ...
- ACM 阶乘之和
阶乘之和 时间限制:3000 ms | 内存限制:65535 KB 难度:3 描述 给你一个非负数整数n,判断n是不是一些数(这些数不允许重复使用,且为正数)的阶乘之和,如9=1!+2!+3! ...
- 阶乘之和--nyoj91
描述 给你一个非负数整数n,判断n是不是一些数(这些数不允许重复使用,且为正数)的阶乘之和,如9=1!+2!+3!,如果是,则输出Yes,否则输出No: 输入 第一行有一个整数0<m<10 ...
- nyoj 91 阶乘之和
点击打开链接 阶乘之和 时间限制:3000 ms | 内存限制:65535 KB 难度: 描述 给你一个非负数整数n,判断n是不是一些数(这些数不允许重复使用,且为正数)的阶乘之和,如9=1!+2 ...
随机推荐
- intellij配置github
一.在IDEA中设置Git,在File-->Setting->Version Control-->Git-->Path to Git executable选择你的git安装后的 ...
- 为什么说String是线程安全的
String是final修饰的类,是不可变的,所以是线程安全的. 一.Java String类为什么是final的? 1.为了实现字符串池 2.为了线程安全 3.为了实现String可以创建HashC ...
- 计算机网络之DDOS
1.什么是DDOS DDOS(Distributed Denial of Service),中文意思为“分布式拒绝服务”,就是利用大量合法的分布式服务器对目标发送请求,从而导致正常合法用户无法获得服务 ...
- openstack Rocky 社区版部署1.3 安装OpenStack packages
1 installing the Rocky release on all nodes. yum install centos-release-openstack-rocky 安装之后,会在/etc/ ...
- JavaScript基础函数的配置对象Configuration Objects(020)
配置对象通常用在API库的实现中,当程序中需要编写要多次的模块,也可以采用这种模式.这种模式的好处是接口明确,扩展方便.比如,一个 addPerson在设计的最初需要两个参数作为初始化时人的姓名: f ...
- python 的迭代
字典的迭代: #创建字典 dict={'a':1,'b':2,'c':3} #key和value的迭代 for key,value in dict.items(): print(key,':',val ...
- 01-springboot整合elasticsearch初识
1.elasticsearch 1.es简介 Elasticsearch 是一个分布式.高扩展.高实时的搜索与数据分析引擎.它能很方便的使大量数据具有搜索.分析和探索的能力.充分利用Elas ...
- (三)ansible playbook
一,YAML语法 YAML的语法和其他高阶语言类似并且可以简单表达清单.散列表.标量等数据结构.(列表用横杆表示,键值对用冒号分割,键值对里又可以嵌套另外的键值对) YAML文件扩展名通常为.yaml ...
- Django---进阶5
目录 单表操作 必知必会13条 测试脚本 查看内部sql语句的方式 神奇的双下划线查询 一对多外键增删改查 多对多外键增删改查 正反向的概念 多表查询 子查询(基于对象的跨表查询) 联表查询(基于双下 ...
- day30 继承、派生与多态,类中方法和内置函数
目录 一.多继承出现的问题(mixins机制) 二.派生与方法重用 三.多态 1 什么是多态 2 为什么要有多态 3 python中多态的鸭子类型 四.绑定方法与非绑定方法 1 绑定方法 1.1对象的 ...
