Notes on Probabilistic Latent Semantic Analysis (PLSA)
转自:http://www.hongliangjie.com/2010/01/04/notes-on-probabilistic-latent-semantic-analysis-plsa/
I highly recommend you read the more detailed version of http://arxiv.org/abs/1212.3900
Formulation of PLSA
There are two ways to formulate PLSA. They are equivalent but may lead to different inference process.
Let’s see why these two equations are equivalent by using Bayes rule.
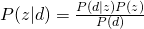
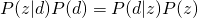
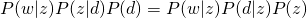
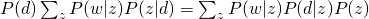
The whole data set is generated as (we assume that all words are generated independently):
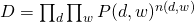
The Log-likelihood of the whole data set for (1) and (2) are:
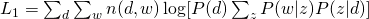
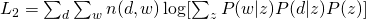
EM
For 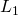 or
or 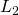 , the optimization is hard due to the log of sum. Therefore, an algorithm called Expectation-Maximization is usually employed. Before we introduce anything about EM, please note that EM is only guarantee to find a local optimum (although it may be a global one).
, the optimization is hard due to the log of sum. Therefore, an algorithm called Expectation-Maximization is usually employed. Before we introduce anything about EM, please note that EM is only guarantee to find a local optimum (although it may be a global one).
First, we see how EM works in general. As we shown for PLSA, we usually want to estimate the likelihood of data, namely 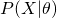 , given the paramter
, given the paramter 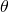 . The easiest way is to obtain a maximum likelihood estimator by maximizing
. The easiest way is to obtain a maximum likelihood estimator by maximizing 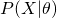 . However, sometimes, we also want to include some hidden variables which are usually useful for our task. Therefore, what we really want to maximize is
. However, sometimes, we also want to include some hidden variables which are usually useful for our task. Therefore, what we really want to maximize is 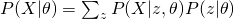 , the complete likelihood. Now, our attention becomes to this complete likelihood. Again, directly maximizing this likelihood is usually difficult. What we would like to show here is to obtain a lower bound of the likelihood and maximize this lower bound.
, the complete likelihood. Now, our attention becomes to this complete likelihood. Again, directly maximizing this likelihood is usually difficult. What we would like to show here is to obtain a lower bound of the likelihood and maximize this lower bound.
We need Jensen’s Inequality to help us obtain this lower bound. For any convex function 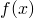 , Jensen’s Inequality states that :
, Jensen’s Inequality states that :
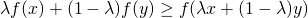
Thus, it is not difficult to show that :
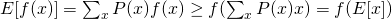
and for concave functions (like logarithm), it is :
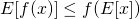
Back to our complete likelihood, we can obtain the following conclusion by using concave version of Jensen’s Inequality :
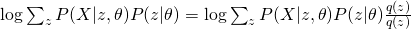
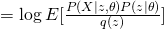
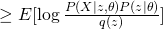
Therefore, we obtained a lower bound of complete likelihood and we want to maximize it as tight as possible. EM is an algorithm that maximize this lower bound through a iterative fashion. Usually, EM first would fix current 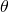 value and maximize
value and maximize 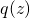 and then use the new
and then use the new 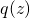 value to obtain a new guess on
value to obtain a new guess on 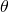 , which is essentially a two stage maximization process. The first step can be shown as follows:
, which is essentially a two stage maximization process. The first step can be shown as follows:
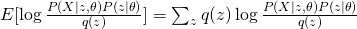
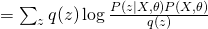
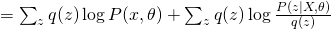
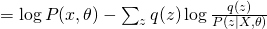
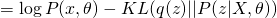
The first term is the same for all  . Therefore, in order to maximize the whole equation, we need to minimize KL divergence between
. Therefore, in order to maximize the whole equation, we need to minimize KL divergence between 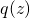 and
and 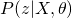 , which eventually leads to the optimum solution of
, which eventually leads to the optimum solution of 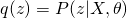 . So, usually for E-step, we use current guess of
. So, usually for E-step, we use current guess of 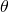 to calculate the posterior distribution of hidden variable as the new update score. For M-step, it is problem-dependent. We will see how to do that in later discussions.
to calculate the posterior distribution of hidden variable as the new update score. For M-step, it is problem-dependent. We will see how to do that in later discussions.
Another explanation of EM is in terms of optimizing a so-called Q function. We devise the data generation process as 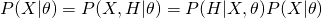 . Therefore, the complete likelihood is modified as:
. Therefore, the complete likelihood is modified as:
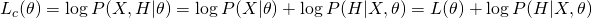
Think about how to maximize 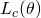 . Instead of directly maximizing it, we can iteratively maximize
. Instead of directly maximizing it, we can iteratively maximize 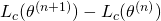 as :
as :
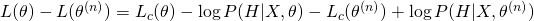
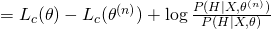
Now take the expectation of this equation, we have:

The last term is always non-negative since it can be recognized as the KL-divergence of 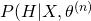 and
and 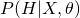 . Therefore, we obtain a lower bound of Likelihood :
. Therefore, we obtain a lower bound of Likelihood :
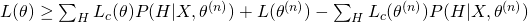
The last two terms can be treated as constants as they do not contain the variable 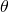 , so the lower bound is essentially the first term, which is also sometimes called as “Q-function”.
, so the lower bound is essentially the first term, which is also sometimes called as “Q-function”. 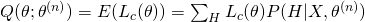
EM of Formulation 1
In case of Formulation 1, let us introduce hidden variables 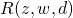 to indicate which hidden topic
to indicate which hidden topic  is selected to generated
is selected to generated 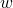 in
in 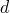 (
(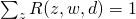 ). Therefore, the complete likelihood can be formulated as :
). Therefore, the complete likelihood can be formulated as :
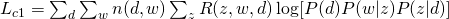
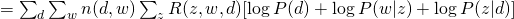
From the equation above, we can write our Q-function for the complete likelihood 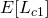 :
:
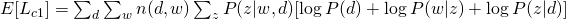
For E-step, simply using Bayes Rule, we can obtain:
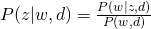
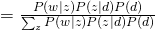
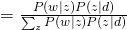
For M-step, we need to maximize Q-function, which needs to be incorporated with other constraints:
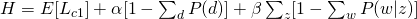

and take all derivatives:
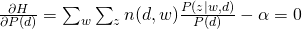
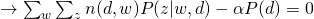
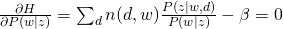
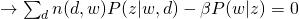
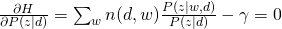
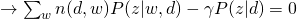
Therefore, we can easily obtain:
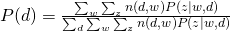
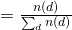
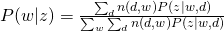
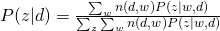
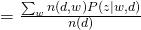
EM of Formulation 2
Use similar method to introduce hidden variables to indicate which  is selected to generated
is selected to generated 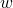 and
and 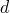 and we can have the following complete likelihood :
and we can have the following complete likelihood :
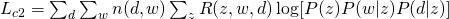
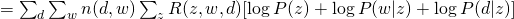
Therefore, the Q-function 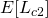 would be :
would be :
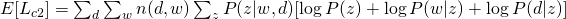
For E-step, again, simply using Bayes Rule, we can obtain:
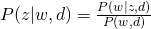
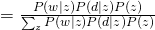
For M-step, we maximize the constraint version of Q-function:
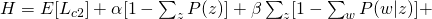
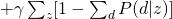
and take all derivatives:
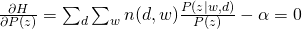
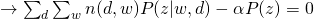
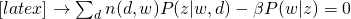
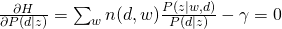
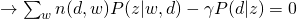
Therefore, we can easily obtain:
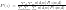
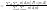
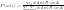
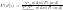
Notes on Probabilistic Latent Semantic Analysis (PLSA)的更多相关文章
- NLP —— 图模型(三)pLSA(Probabilistic latent semantic analysis,概率隐性语义分析)模型
LSA(Latent semantic analysis,隐性语义分析).pLSA(Probabilistic latent semantic analysis,概率隐性语义分析)和 LDA(Late ...
- 主题模型之概率潜在语义分析(Probabilistic Latent Semantic Analysis)
上一篇总结了潜在语义分析(Latent Semantic Analysis, LSA),LSA主要使用了线性代数中奇异值分解的方法,但是并没有严格的概率推导,由于文本文档的维度往往很高,如果在主题聚类 ...
- Latent semantic analysis note(LSA)
1 LSA Introduction LSA(latent semantic analysis)潜在语义分析,也被称为LSI(latent semantic index),是Scott Deerwes ...
- 主题模型之潜在语义分析(Latent Semantic Analysis)
主题模型(Topic Models)是一套试图在大量文档中发现潜在主题结构的机器学习模型,主题模型通过分析文本中的词来发现文档中的主题.主题之间的联系方式和主题的发展.通过主题模型可以使我们组织和总结 ...
- Latent Semantic Analysis (LSA) Tutorial 潜语义分析LSA介绍 一
Latent Semantic Analysis (LSA) Tutorial 译:http://www.puffinwarellc.com/index.php/news-and-articles/a ...
- 潜语义分析(Latent Semantic Analysis)
LSI(Latent semantic indexing, 潜语义索引)和LSA(Latent semantic analysis,潜语义分析)这两个名字其实是一回事.我们这里称为LSA. LSA源自 ...
- 潜在语义分析Latent semantic analysis note(LSA)原理及代码
文章引用:http://blog.sina.com.cn/s/blog_62a9902f0101cjl3.html Latent Semantic Analysis (LSA)也被称为Latent S ...
- 海量数据挖掘MMDS week4: 推荐系统之隐语义模型latent semantic analysis
http://blog.csdn.net/pipisorry/article/details/49256457 海量数据挖掘Mining Massive Datasets(MMDs) -Jure Le ...
- Latent Semantic Analysis(LSA/ LSI)原理简介
LSA的工作原理: How Latent Semantic Analysis Works LSA被广泛用于文献检索,文本分类,垃圾邮件过滤,语言识别,模式检索以及文章评估自动化等场景. LSA其中一个 ...
随机推荐
- 【JavaScript学习笔记】if使用
<html> <body> <script language="JavaScript"> var a=4; var b=2; if(a==3) ...
- 多层感知机及其BP算法(Multi-Layer Perception)
Deep Learning 近年来在各个领域都取得了 state-of-the-art 的效果,对于原始未加工且单独不可解释的特征尤为有效,传统的方法依赖手工选取特征,而 Neural Network ...
- 顶 兼容各种浏览器js折叠菜单
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...
- Selenium IDE- 不同的浏览器
Selenium IDE- 不同的浏览器 Selenium IDE脚本只能对火狐的工具Firefox插件运行测试.使用Selenium-IDE开发的测试可以对其他浏览器所保存为Selenium网络驱动 ...
- 你可能不知道的30个Python语言的特点技巧
1 介绍 从我开始学习Python时我就决定维护一个经常使用的“窍门”列表.不论何时当我看到一段让我觉得“酷,这样也行!”的代码时(在一个例子中.在StackOverflow.在开源码软件中,等等), ...
- ajax 访问--提高安全性
首先受到struts token的启发,产生了客户端发起的ajax请求进行验证的想法,大致思路是客户端每次请求产生一个key ,然后服务端接收到key,然后解析,判断是否为合法key, 对于不带key ...
- ninject学习笔记一:IOC的实现
这篇文章主要介绍ninject在IOC方面的实现,至于IOC的含义,网络资源很丰富,我这儿就不再赘述了.官方的文档其实挺好的,只是本人英语很烂,看起来比较费劲,下面这些东西是看官方的代码推敲的,我觉得 ...
- [转]Python文件操作
前言 这里的“文件”不单单指磁盘上的普通文件,也指代任何抽象层面上的文件.例如:通过URL打开一个Web页面“文件”,Unix系统下进程间通讯也是通过抽象的进程“文件”进行的.由于使用了统一的接口,从 ...
- 项目常用jquery/easyui函数小结
#项目常用jquery/easyui函数小结 ##背景 项目中经常需要使用到一些功能,封装.重构.整理后形成代码沉淀,在此进行分享 ##代码 ```javascript /** * @author g ...
- brew 更新
更新: brew update brew update —system 安装, 如:brew install unrar 卸载, 如:brew uninstall unrar


