hdu 4828 Grids 卡特兰数+逆元

Grids

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65535/65535 K (Java/Others)

Problem Description

　　度度熊最近很喜欢玩游戏。这一天他在纸上画了一个2行N列的长方形格子。他想把1到2N这些数依次放进去，但是为了使格子看起来优美，他想找到使每行每列都递增的方案。不过画了很久，他发现方案数实在是太多了。度度熊想知道，有多少种放数字的方法能满足上面的条件？

 

Input

　　第一行为数据组数T(1<=T<=100000)。
　　然后T行，每行为一个数N(1<=N<=1000000)表示长方形的大小。

 

Output

　　对于每组数据，输出符合题意的方案数。由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。

 

Sample Input

2
1
3

 

Sample Output

Case #1:
1
Case #2:
5

Hint

对于第二组样例，共5种方案，具体方案为：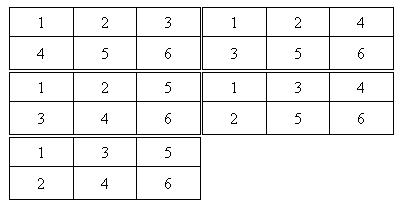

 

Source

2014年百度之星程序设计大赛 - 初赛（第一轮）

思路：卡特兰数；

　　　

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
const int N=2e5+10,M=4e6+10,inf=1e9+10,mod=1e9+7;
const ll INF=1e18+10;
ll a[M];
ll inv[M];
void init()
{
    inv[1] = 1;
    for(int i=2;i<=1000010;i++)
    {
        if(i >= mod)break;
        inv[i] = (mod - mod / i) * inv[mod % i]% mod;
    }
}
ll pows(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)ans*=a,ans%=mod;
        a*=a;
        a%=mod;
        b>>=1;
    }
    return ans;
}
int main()
{
    a[0]=1;
    init();
    for(ll i=1;i<=1000000;i++)
    {
        a[i]=(((a[i-1]*(4*i-2))%mod)*inv[i+1])%mod;
    }
    int T,cas=1;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        scanf("%d",&n);
        printf("Case #%d:\n%lld\n",cas++,a[n]);
    }
    return 0;
}