leetcode：Count Primes

Description:Count the number of prime numbers less than a non-negative number, n.

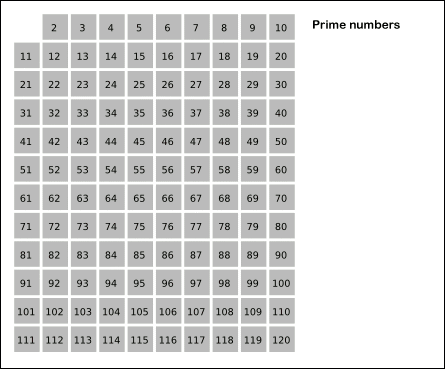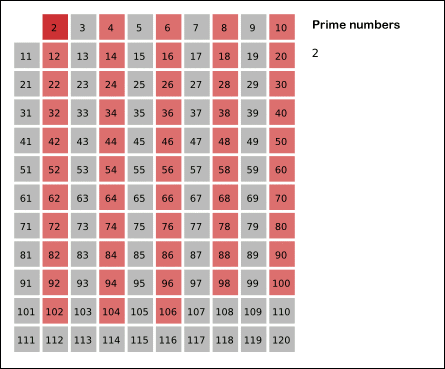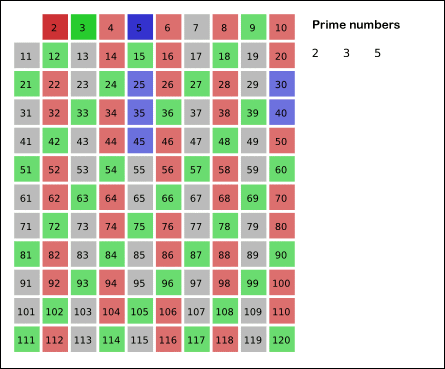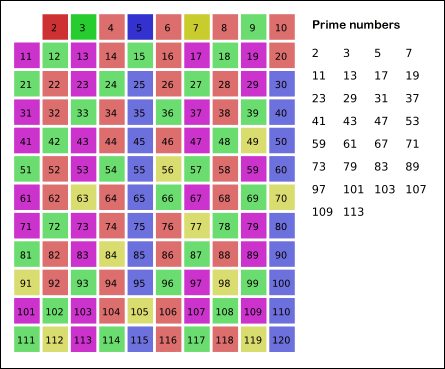
本题给定一个非负数n，让我们求小于n的质数的个数，解题方法就在第二个提示埃拉托斯特尼筛法Sieve of Eratosthenes中，这个算法的过程如下图所示，我们从2开始遍历到根号n，先找到第一个质数2，然后将其所有的倍数全部标记出来，然后到下一个质数3，标记其所有倍数，一次类推，直到根号n，此时数组中未被标记的数字就是质数。我们需要一个n-1长度的bool型数组来记录每个数字是否被标记，长度为n-1的原因是题目说是小于n的质数个数，并不包括n。 然后我们用两个for循环来实现埃拉托斯特尼筛法，难度并不是很大，代码如下所示：

class Solution {
public:
    int countPrimes(int n) {
        vector<bool> num(n - 1, true);
        num[0] = false;
        int res = 0, limit = sqrt(n);
        for (int i = 2; i <= limit; ++i) {
            if (num[i - 1]) {
                for (int j = i * i; j < n; j += i) {
                    num[j - 1] = false;
                }
            }
        }
        for (int j = 0; j < n - 1; ++j) {
            if (num[j]) ++res;
        }
        return res;
    }
};

其他解法：

1、（56ms）
class Solution {
public:
    int countPrimes(int n) {
        if (n < 2)
        {
            return 0;
        }
        bool prime[n];
        memset(prime, true, n*sizeof(bool));  //memset：作用是在一段内存块中填充某个给定的值，第三个参数指定块的大小
        prime[0] = false;
        prime[1] = false;  

        int result = 0;
        int limit = sqrt(n);  

        for (int i = 2; i <= limit; i++)
        {
            if (prime[i])
            {
                for (int j = i*i; j < n; j += i)
                {
                    prime[j] = false;
                }
            }
        }  

        for (int i = 0; i < n; i++)
        {
            if (prime[i])
            {
                result++;
            }
        }  

        return result;
    }
};

　　

2、（86ms）
class Solution {
public:
    int countPrimes(int n) {
        if(n<3)
            return 0;
        int *flag=new int[n];
        fill(flag,flag+n,1);//fill（）作用是设置指定范围【flag，flag+n）内的元素值为1
        int c=n-2,m=n/2;//1和n都不在，故为n-2
        for(int i=2;i<=m;i++)
        {
            if(flag[i])
            {
                for(int j=2;i*j<n;j++)
                {
                    if(flag[i*j])
                    {
                        flag[i*j]=0;
                        c--;
                    }
                }
            }
        }
        delete []flag;
        return c;
    }
};