树的prufer编码

prufer是无根树的一种编码方式，一棵无根树和一个prufer编码唯一对应，也就是一棵树有唯一的prufer编码，而一个prufer编码对应一棵唯一的树。

第一部分：树编码成prufer序列。

树编码成prufer序列的方式是：prufer序列初始为空。每次从树上选出一个编号最小的叶子节点，然后将与该叶子节点相邻的那个节点的编号写入prufer序列的末尾，之后从树上删掉这个叶子节点。循环这个步骤n-2次，最后得到一个长度为n-2的prufer序列（此时树中只有一条边，我们就不管它了）。

我们以下面这个树为例。

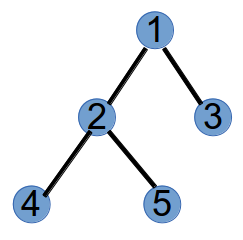
step1:编号最小的叶子节点为3，将与其相连的节点1加到prufer的末尾，并将3从树上删掉，此时prufer序列为(1)，树变为如下：

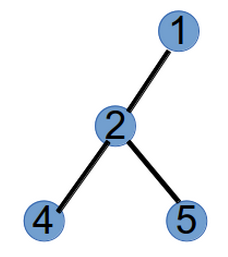
step2:编号最小的叶子节点为1，将与其相连的节点2加到prufer末尾，此时prufer序列为(1,2),并将节点1删掉，树变为如下：

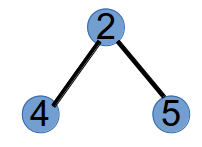
step3:编号最小的叶子节点为4，将与其相连的节点2加入到prufer的末尾，此时prufer序列为(1,2,2)，并将节点4删掉，树变为如下：

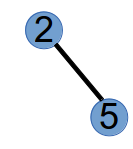
此时，结束，我们得到了prufer序列为(1,2,2)。

第二部分：由prufer序列得到树。首先，将每个节点的度数设为1加上该节点在prufer序列中出现的次数。然后以下循环执行n-2次。第i次循环，选择此时度数为1的编号最小的节点u，将其与此时prufer序列的第i个元素v连边，然后将u和v的度数都减去1。这n-2次执行完之后，仅剩下两个节点他们的度数都是1，将这两个点连边，这样就得到一个有n-1条边的树。

下面，我们以上面的prufer序列为例还原这个树。初始的prufer为(1,2,2)，初始的度数为：

step1：选择度数为1的最小编号的节点3与prufer的第一个元素1连边，并将3和1的度数都减去1，得到树和新的度数：

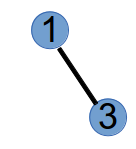
step2：选择度数为1的最小节点1和prufer中的第二个元素2连边，并将1和2的度数都减去1，得到树和新的度数：

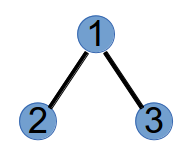
step3：选择度数为1的最小节点4和prufer中的第三个元素2连边，并将4和2的度数都减去1，得到树和新的度数：

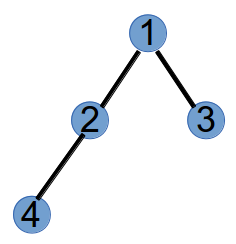
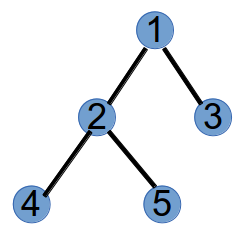
最后，将仅有的度数为1的两个节点2和5，连边，得到：