Java实现拓扑排序

1 问题描述

给定一个有向图，求取此图的拓扑排序序列。

那么，何为拓扑排序？

定义：将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv，在最后的排序结果中，顶点u总是在顶点v的前面。

2 解决方案

2.1 基于减治法实现

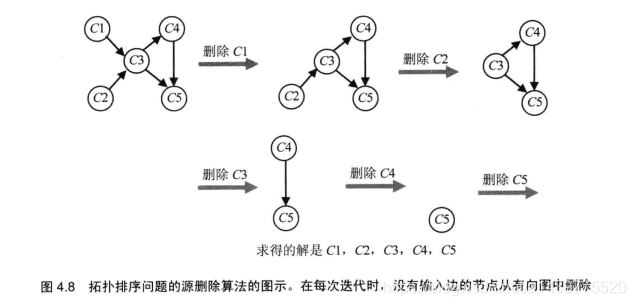
实现原理：不断地做这样一件事，在余下的有向图中求取一个源（source）（PS：定义入度为0的顶点为有向图的源），它是一个没有输入边的顶点，然后把它和所有从它出发的边都删除。（如果有多个这样的源，可以任意选择一个。如果这样的源不存在，算法停止，此时该问题无解），下面给出《算法设计与分析基础》第三版上一个配图：

package com.liuzhen.chapterFour;

import java.util.Stack;

public class TopologicalSorting {
    //方法1：基于减治法：寻找图中入度为0的顶点作为即将遍历的顶点，遍历完后，将此顶点从图中删除
    /*
     * 参数adjMatrix:给出图的邻接矩阵值
     * 参数source:给出图的每个顶点的入度值
     * 该函数功能：返回给出图的拓扑排序序列
     */
    public char[] getSourceSort(int[][] adjMatrix,int[] source){
        int len = source.length;          //给出图的顶点个数
        char[] result = new char[len];   //定义最终返回路径字符数组
        int count = 0;                  //用于计算当前遍历的顶点个数
        boolean judge = true;
        while(judge){
            for(int i = 0;i < source.length;i++){
                if(source[i] == 0){                 //当第i个顶点入度为0时，遍历该顶点
                    result[count++] = (char) ('a'+i);
                    source[i] = -1;                  //代表第i个顶点已被遍历
                    for(int j = 0;j < adjMatrix[0].length;j++){   //寻找第i个顶点的出度顶点
                        if(adjMatrix[i][j] == 1)
                            source[j] -= 1;          //第j个顶点的入度减1
                    }
                }
            }
            if(count == len)
                judge = false;
        }
        return result;
    }
    /*
     * 参数adjMatrix:给出图的邻接矩阵值
     * 函数功能：返回给出图每个顶点的入度值
     */
    public int[] getSource(int[][] adjMatrix){
        int len = adjMatrix[0].length;
        int[] source = new int[len];
        for(int i = 0;i < len;i++){
            //若邻接矩阵中第i列含有m个1，则在该列的节点就包含m个入度，即source[i] = m
            int count = 0;
            for(int j = 0;j < len;j++){
                if(adjMatrix[j][i] == 1)
                    count++;
            }
            source[i] = count;
        }
        return source;
    }

    public static void main(String[] args){
        TopologicalSorting test = new TopologicalSorting();
        int[][] adjMatrix = {{0,0,1,0,0},{0,0,1,0,0},{0,0,0,1,1},{0,0,0,0,1},{0,0,0,0,0}};
        int[] source = test.getSource(adjMatrix);
        System.out.println("给出图的所有节点（按照字母顺序排列）的入度值：");
        for(int i = 0;i < source.length;i++)
            System.out.print(source[i]+"\t");
        System.out.println();
        char[] result = test.getSourceSort(adjMatrix, source);

        System.out.println("给出图的拓扑排序结果：");
        for(int i = 0;i < result.length;i++)
            System.out.print(result[i]+"\t");
    }
}

运行结果：

给出图的所有节点（按照字母顺序排列）的入度值：
0    0    2    1    2
给出图的拓扑排序结果：
a    b    c    d    e

2.2 基于深度优先查找实现

引用自网友博客中一段解释：

除了使用上面2.1中所示算法之外，还能够借助深度优先遍历来实现拓扑排序。这个时候需要使用到栈结构来记录拓扑排序的结果。

同样摘录一段维基百科上的伪码：

L ← Empty list that will contain the sorted nodes

S ← Set of all nodes with no outgoing edges

for each node n in S do
    visit(n)
function visit(node n)
    if n has not been visited yet then
        mark n as visited
        for each node m with an edgefrom m to ndo
            visit(m)
        add n to L

DFS的实现更加简单直观，使用递归实现。利用DFS实现拓扑排序，实际上只需要添加一行代码，即上面伪码中的最后一行：add n to L。

需要注意的是，将顶点添加到结果List中的时机是在visit方法即将退出之时。

此处重点在于理解：上面伪码中的最后一行：add n to L，对于这一行的理解重点在于对于递归算法执行顺序的理解，递归执行顺序的核心包括两点：1.先执行递归，后进行回溯；2.遵循栈的特性，先进后出。此处可以参考本人另外一篇博客：递归执行顺序的探讨

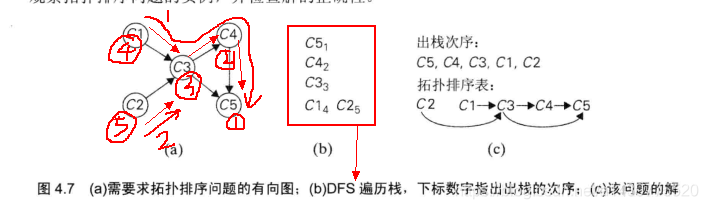
下面请看一个出自《算法设计与分析基础》第三版上一个配图：

package com.liuzhen.chapterFour;

import java.util.Stack;

public class TopologicalSorting {

    //方法2：基于深度优先查找发（DFS）获取拓扑排序
    public int count1 = 0;
    public Stack<Character> result1;
    /*
     * adjMatrix是待遍历图的邻接矩阵
     * value是待遍历图顶点用于是否被遍历的判断依据，0代表未遍历，非0代表已被遍历
     */
    public void dfs(int[][] adjMatrix,int[] value){
        result1 = new Stack<Character>();
        for(int i = 0;i < value.length;i++){
            if(value[i] == 0)
                dfsVisit(adjMatrix,value,i);
        }
    }
     /*
    * adjMatrix是待遍历图的邻接矩阵
    * value是待遍历图顶点用于是否被遍历的判断依据，0代表未遍历，非0代表已被遍历
    * number是当前正在遍历的顶点在邻接矩阵中的数组下标编号
    */
    public void dfsVisit(int[][] adjMatrix,int[] value,int number){
        value[number] = ++count1;               //把++count1赋值给当前正在遍历顶点判断值数组元素，变为非0，代表已被遍历
        for(int i = 0;i < value.length;i++){
            if(adjMatrix[number][i] == 1 && value[i] == 0)         //当，当前顶点的相邻有相邻顶点可行走且其为被遍历
                dfsVisit(adjMatrix,value,i);   //执行递归，行走第i个顶点
        }
        char temp = (char) ('a' + number);
        result1.push(temp);
    }

    public static void main(String[] args){
        TopologicalSorting test = new TopologicalSorting();
        int[][] adjMatrix = {{0,0,1,0,0},{0,0,1,0,0},{0,0,0,1,1},{0,0,0,0,1},{0,0,0,0,0}};

        int[] value = new int[5];
        test.dfs(adjMatrix, value);
        System.out.println();
        System.out.println("使用ＤＦＳ方法得到拓扑排序序列的逆序：");
        System.out.println(test.result1);
        System.out.println("使用ＤＦＳ方法得到拓扑排序序列：");
        while(!test.result1.empty())
            System.out.print(test.result1.pop()+"\t");

    }
}

运行结果：

使用ＤＦＳ方法得到拓扑排序序列的逆序：
[e, d, c, a, b]
使用ＤＦＳ方法得到拓扑排序序列：
b    a    c    d    e