【30分钟学完】canvas动画|游戏基础(6)：坐标旋转探究

前言

本篇主要讲坐标旋转及其应用，这是编程动画必不可少的技术。
阅读本篇前请先打好前面的基础。
本人能力有限，欢迎牛人共同讨论，批评指正。

坐标旋转

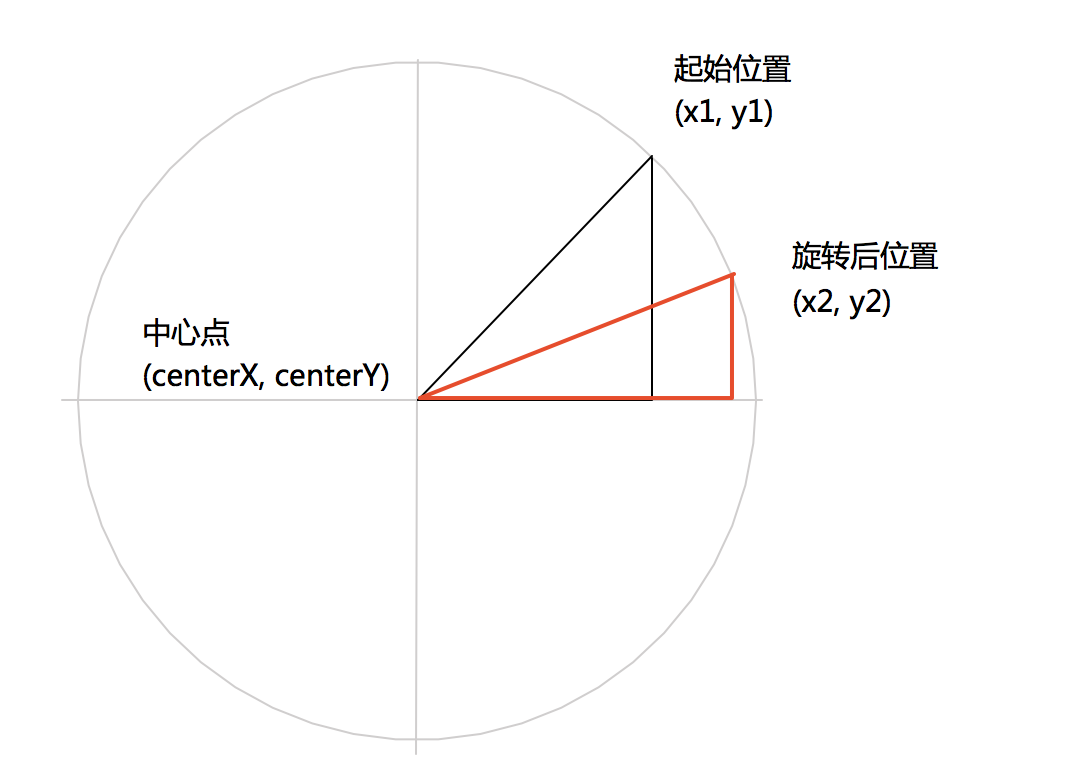
模拟场景：已知一个中心点（centerX,centerY），旋转前物体ball（x1,y1），旋转弧度（rotation）；求旋转后物体（x2,y2）。（如下图）

坐标旋转就是说围绕某个点旋转坐标，我们要依据旋转的角度（弧度），计算出物体旋转前后的坐标，一般有两种方法：

简单坐标旋转

灵活运用前章节的三角函数知识可以很容易解决，基本思路：

计算物体初始相对于中心点的位置；
使用atan2计算弧度angle；
使用勾股定理计算半径radius；
angle+rotation后使用cos计算旋转后x轴位置，用sin计算旋转后y轴位置。

下面是示例是采用这种方法的圆周运动，其中vr为ball相对于中心点的弧度变化速度，由于旋转半径是固定的，所以没有在动画循环里每次都获取。
完整示例：简单坐标旋转演示

/**

 * 简单坐标旋转演示

 * */

window.onload = function () {

  const canvas = document.getElementById('canvas');

  const context = canvas.getContext('2d');

  const ball = new Ball();

  ball.x = 300;

  ball.y = 200;

  // 弧度变化速度

  const vr = 0.05;

  // 中心点位置设定在画布中心

  const centerX = canvas.width / 2;

  const centerY = canvas.height / 2;

  // ball相对与中心点的距离

  const dx = ball.x - centerX;

  const dy = ball.y - centerY;

  // ball相对与中心点的弧度

  let angle = Math.atan2(dy, dx);

  // 旋转半径

  const radius = Math.sqrt(dx ** 2 + dy ** 2);

  (function drawFrame() {

    window.requestAnimationFrame(drawFrame, canvas);

    context.clearRect(0, 0, canvas.width, canvas.height);

    ball.x = centerX + Math.cos(angle) * radius;

    ball.y = centerY + Math.sin(angle) * radius;

    angle += vr;

    ball.draw(context);

  }());

};

坐标旋转公式

上面的方法对于单个物体来说是很合适的，特别是角度和半径只需计算一次的情况。但是在更动态的场景中，可能需要旋转多个物体，而他们相对于中心点的位置各不相同。所以每一帧都要计算每个物体的距离、角度和半径，然后把vr累加在角度上，最后计算物体新的坐标。这样显然不会是优雅的做法。
理想的做法是用数学方法推导出旋转角度与位置的关系，直接每次代入计算即可。推导过程如下图：

其实推导过程不重要，我们只需要记住如下两组公式，其中dx2和dy2是ball结束点相对于中心点的距离，所以得到物体结束点，还要分别加上中心点坐标。

// 正向选择

dx2 = (x1 - centerX) * cos(rotation) - (y1 - centerY) * sin(rotation)

dy2 = (y1 - centerY) * cos(rotation) + (x1 - centerX) * sin(rotation)

// 反向选择

dx2 = (x1 - centerX) * cos(rotation) + (y1 - centerY) * sin(rotation)

dy2 = (y1 - centerY) * cos(rotation) - (x1 - centerX) * sin(rotation)

下面是示例是采用这种方法的圆周运动，其中dx1和dy1是ball起始点相对于中心点的距离，dx2和dy2是ball结束点相对于中心点的距离。
完整示例：高级坐标旋转演示

/**

 * 高级坐标旋转演示

 * */

window.onload = function () {

  const canvas = document.getElementById('canvas');

  const context = canvas.getContext('2d');

  const ball = new Ball();

  ball.x = 300;

  ball.y = 200;

  // 弧度变化速度

  const vr = 0.05;

  // 中心点位置设定在画布中心

  const centerX = canvas.width / 2;

  const centerY = canvas.height / 2;

  // 由于vr是固定的可以先计算正弦和余弦

  const cos = Math.cos(vr);

  const sin = Math.sin(vr);

  (function drawFrame() {

    window.requestAnimationFrame(drawFrame, canvas);

    context.clearRect(0, 0, canvas.width, canvas.height);

    // ball相对与中心点的距离

    const dx1 = ball.x - centerX;

    const dy1 = ball.y - centerY;

    // 代入公式求出ball在结束相对与中心点的距离

    const dx2 = dx1 * cos - dy1 * sin;

    const dy2 = dy1 * cos + dx1 * sin;

    // 求出x2，y2

    ball.x = centerX + dx2;

    ball.y = centerY + dy2;

    ball.draw(context);

  }());

};

斜面反弹

前面的章节中我们介绍过越界的一种处理办法是反弹，由于边界是矩形，反弹面垂直或水平，所以可以直接将对应轴的速度取反即可，但对于非垂直或水平的反弹面这种方法是不适用的。
坐标旋转常见的应用就是处理这种情况，将不规律方向的复杂问题简单化。
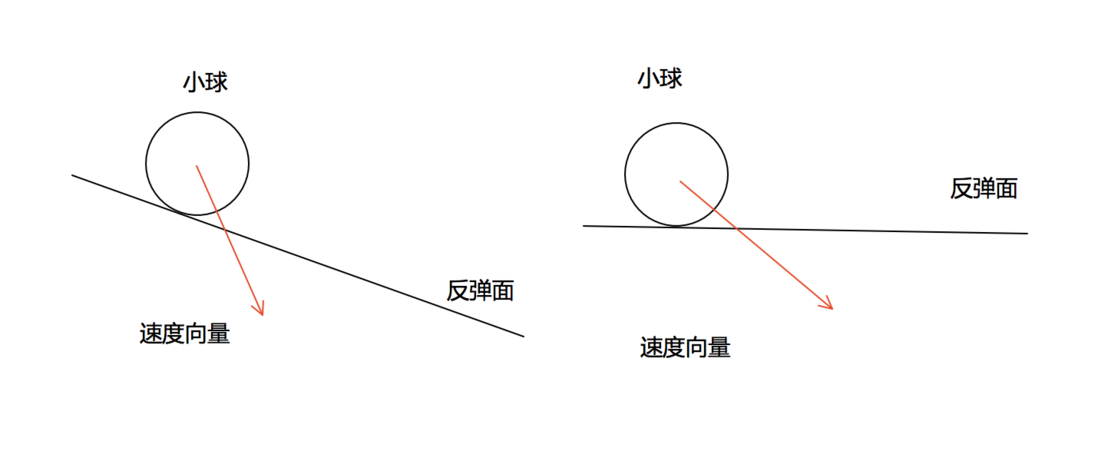
基本思路：（旋转前后如图）

使用旋转公式，旋转整个系统，将斜面场景转变为水平场景；
在水平场景中处理反弹；
再旋转回来。

示例是一个球掉落到一条线上，球受到重力加速度影响下落，碰到斜面就会反弹，每次反弹都会损耗速度。
完整示例：斜面反弹示例

window.onload = function () {

  const canvas = document.getElementById('canvas');

  const context = canvas.getContext('2d');

  const ball = new Ball();

  // line类构造函数参数（开始点x轴坐标，开始点y轴坐标，结束点x轴坐标，结束点y轴坐标）

  const line = new Line(0, 0, 500, 0);

  // 设置重力加速度

  const gravity = 0.2;

  // 设置反弹系数

  const bounce = -0.6;

  ball.x = 100;

  ball.y = 100;

  line.x = 0;

  line.y = 200;

  line.rotation = 10 * Math.PI / 180;

  const cos = Math.cos(line.rotation);

  const sin = Math.sin(line.rotation);

  (function drawFrame() {

    window.requestAnimationFrame(drawFrame, canvas);

    context.clearRect(0, 0, canvas.width, canvas.height);

    ball.vy += gravity;

    ball.x += ball.vx;

    ball.y += ball.vy;

    // 获取ball与line的相对位置

    let x1 = ball.x - line.x;

    let y1 = ball.y - line.y;

    // 旋转坐标系（反向）

    let y2 = y1 * cos - x1 * sin;

    // 依据旋转值执行反弹

    if (y2 > -ball.radius) {

      // 旋转坐标系（反向）

      const x2 = x1 * cos + y1 * sin;

      // 旋转速度（反向）

      const vx1 = ball.vx * cos + ball.vy * sin;

      let vy1 = ball.vy * cos - ball.vx * sin;

      y2 = -ball.radius;

      vy1 *= bounce;

      // 将所有东西回转（正向）

      x1 = x2 * cos - y2 * sin;

      y1 = y2 * cos + x2 * sin;

      ball.vx = vx1 * cos - vy1 * sin;

      ball.vy = vy1 * cos + vx1 * sin;

      ball.x = line.x + x1;

      ball.y = line.y + y1;

    }

    ball.draw(context);

    line.draw(context);

  }());

};