Trie图（AC自动机）总结

AC自动机构建完成后，某个节点沿着Fail链向上能从长到短走到自己的所有后缀。一般的，遍历主串进行匹配，就是在Trie图上定向移动的过程。

构造（一遍 BFS）

 void build_AC()
 {
     int u=;
     for(int i=;i<;i++)
         if(ch[u][i])q[r++]=ch[u][i];
     while(l<r)
     {
         u=q[l++];
         for(int i=;i<;i++)
             if(ch[u][i])
             {
                 fail[ch[u][i]]=ch[fail[u]][i];
                 flag[ch[u][i]]|=flag[fail[ch[u][i]]];
                 q[r++]=ch[u][i];
             }
             else
                 ch[u][i]=ch[fail[u]][i];
     }
 }

1、模式匹配

主串从左到右，就顺着每一个字符向下跳，每一次沿着Fail链向上。这样会可重而不漏的得到模式串中的所有子串，视题目要求进行操作即可。

（1）TJOI2013 单词：本人的LJ做法，把所有串建Trie图，再把所有串拿 # 接起来，然后暴力匹配。

2、利用Fail链进行预处理

（1）不可到达（危险）节点标记：一个串的后缀是危险的，它即是危险的

（2）某些统计：到达某个串结尾处相当于匹配了它和它的所有后缀，可以进行一些sigma之类的操作

3、与Trie图性质相关

（SDOI2005 病毒）模拟一个字符串在Trie图上匹配的过程，危险节点不可走。在此基础上找环。

4、AC自动机相关某些题目

（1）HNOI2004 L语言 ：在模式串结尾记LEN，一边模式匹配一边 DP，

（2）USACO2015 删减：在模式串结尾记LEN，维护一个栈，匹配成功时把栈顶上LEN个元素拿走

（3）JSOI2009：密码：在Trie图上进行记忆化搜索（记录所有串的选取状态）输出方案好恶心的

5、Trie图上的DP

一般的，设出如下状态：

：做到主串第 i 个位置，在Trie图上的 j 点，……。

转移： 使用刷表法DP，必要时上矩阵进行优化。

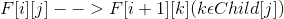
初始状态是 。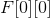

（1）Fzoj DNA修复：不能往危险节点跑，然后直接。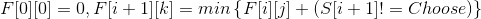

（2）Fzoj 匹配：状压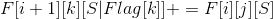，，Flag事先预处理。

（3）Fzoj 中等的字符串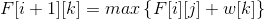：， 构造矩阵转移，类似求 N 条边最长路。

扔一份 暴力DP 的代码：

 void dp()
 {
     for(int i=;i<=n;i++)
         for(int j=;j<=tot;j++)
             f[i][j]=-inf;
     f[][]=;
     for(int i=;i<n;i++)
         for(int j=;j<=tot;j++)
             if(f[i][j]>=)
                 for(int x=;x<;x++)
                 {
                     int k=ch[j][x];
                     f[i+][k]=max(f[i+][k],f[i][j]+num[k]);
                 }
 }

（4）BJOI2016 打字机：不可做

（5）BJOI2017 魔法咒语：1-6号点暴力做，7-8用转移矩阵，9-10类似 Fib 那样进行转移，挺毒瘤的。

6、Fail树性质（Fail 链自下而上的后缀关系）

一般用于解决与多串相关的子串计数问题。

（1）阿狸的打字机：按题意模拟建 Trie 树，按题意模拟在 Trie 图上跑，走到+1离开-1，用 BIT 维护子树和。

（2）COCI2015 Divljak：先对 Alice 的串建 Trie 图，由 Fail 树性质原问题等价于解决“树链求并”的计数问题，解决方法我是抄题解的：对链的各个底端端点按 dfs 序排序，在各个点处 +1，在相邻两点 LCA 处 -1（想一想为啥）。树剖求 LCA 即可。子树和仍然使用 BIT 维护。