luogu P2704 炮兵阵地(经典状态压缩DP)

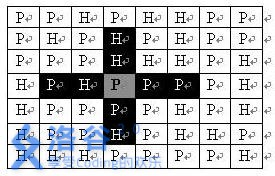
方格有m*n个格子,一共有2^(m+n)种排列,很显然不能使用暴力法,因而选用动态规划求解.

求解DP问题一般有3步,即定义出一个状态 求出状态转移方程 再用算法实现.多数DP题难youguan点在于第2步,而在状态压缩DP中,定义状态也是很关键的一个步骤.有关位运算的基础知识,按位与,按位或,异或等可自行查阅资料,这里仅作简单说明.

<<n == 2的n次方
>>n == /2的n次方
(n>>k) &    // 取出整数n在二进制下的第k位
n & ((<<k)-) // 取出整数n在二进制下的后k位
(i>>j) & k  // i右移j位后和k与运算

很容易想到用二进制数来表示方格,1表示放炮兵,0表示不放.在同一行中,只要没有出现两个炮兵紧邻或者两个炮兵只间隔1个位置的情况,均是合法的状态.故在二进制表示的行01串中删除字串含有"11","101"的原串即可,预处理出合法的01串并存于legal中.

vector<int> legal;
void init() {    // 找到合法的摆放总数
    for(int i = ; i < (<<m); i++) { // 1<<m == pow(2,m),遍历所有情况
        int c1 = , c2 = ; // 3 -> (11) , 5 -> (101)
        bool sub = ;
        for(int j = ; j < m - ; j++) {
            if(((i >> j) & c1) == c1) {
                sub = ;
            }
        }
        for(int j = ; j < m - ; j++) {
            if(((i >> j) & c2) == c2) {
                sub = ;
            }
        }
        if(sub) legal.push_back(i);
    }
}

并用count函数计算每行中的1(炮兵数目):

int count(int x) {
    int cnt = ;
    for(int i = ; i < m; i++) {
        if(((x>>i)&) == ) {
            cnt++;
        }
    }
    return cnt;
}

接下来设计DP状态和状态转移

每一行的状态受该行前两行摆放状态的影响,因此选择dp[i][j][k]表示可行方案数.dp[i][j][k]表示第i行压缩后状态为j,第i-1行压缩后状态为k的情况下前i行最多放多少个炮兵.同时由于dp[102][1050][1050]会MLE,只有80分不过也知足了, 需要将dp改为滚动数组,将第一维每处均%3即可,只记录前两次的状态

读入地图时把每行压缩成一个二进制数,为了便于后续查找可行状态,读入时H对应1,P对应0. 后续遍历了legal中的合法状态时,若与该行的01表示与运算值不为0,即与地图存在冲突.

状态转移方程为dp[本行][前一行][再前一行] = max{dp[前一行][再前一行][再前一行的前一行] + count(本行) , dp[本行][前一行][再前一行]}

完整的代码如下:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + ;

int n, m;
string s;
int mp[];
vector<int> legal;  // 储存所有的合法01串
int dp[][][];

void init() {    // 找到合法的摆放总数
    for(int i = ; i < (<<m); i++) { // 1<<m == pow(2,m)
        int c1 = , c2 = ; // 3 -> (0011) , 5 -> (0101)
        bool sub = ;
        for(int j = ; j < m - ; j++) {
            if(((i >> j) & c1) == c1) {
                sub = ;
            }
        }
        for(int j = ; j < m - ; j++) {
            if(((i >> j) & c2) == c2) {
                sub = ;
            }
        }
        if(sub) legal.push_back(i);
    }
}

int count(int x) {
    int cnt = ;
    for(int i = ; i < m; i++) {
        if(((x>>i)&) == ) {
            cnt++;
        }
    }
    return cnt;
}

int main() {
    cin>>n>>m;
    init();
    // cout<<legal.size()<<endl;
    for(int i = ; i <= n + ; i++) {  // i初值2 避免越界(需考虑到前两行)
        cin>>s;
        for(int j = ; j < m; j++)
            if(s[j] == 'H') mp[i] |= (<<j);
    }
    for(int i = ; i <= n + ; i++) {
        for(auto step : legal) {
            if((step & mp[i]) != ) continue;
            for(auto bst : legal) {
                if((step & bst) != ) continue;
                if((bst & mp[i-]) != ) continue;
                for(auto bbst : legal) {
                    if((step & bbst) != ) continue;
                    if((bbst & mp[i-]) != ) continue;
                    if((bbst & bst) != ) continue;
                    dp[i%][step][bst] = max(dp[(i-)%][bst][bbst] + count(step), dp[i%][step][bst]);
                }
            }
        }
    }
    int res = ;
    for(auto step : legal)
        for(auto bst : legal)
            res = max(res, dp[(n+)%][step][bst]);
    cout<<res<<endl;
}