「ZJOI2006」物流运输

题目

【内存限制：$256MiB$】【时间限制：$1000ms$】

【标准输入输出】【题目类型：传统】【评测方式：文本比较】

---

【题目描述】

物流公司要把一批货物从码头 A 运到码头 B。由于货物量比较大，需要 $n$ 天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线，以便对整个运输过程实施严格的管理和跟踪。

由于各种因素的存在，有的时候某个码头会无法装卸货物。这时候就必须修改运输线路，让货物能够按时到达目的地。但是修改路线是一件十分麻烦的事情，会带来额外的成本，因此物流公司希望能够订一个 $n$ 天的运输计划，使得总成本尽可能地小。

【输入格式】

第一行是四个整数 $n(1\le n\le 100),m(1\le m\le 20),K,e$。$n$ 表示货物运输所需天数，$m$ 表示码头总数，$K$ 表示每次修改运输路线所需成本。

接下来 $e$ 行每行是一条航线描述，包括了三个整数，依次表示航线连接的两个码头编号以及航线长度 $(>0)$。其中码头 A 编号为 $1$，码头 B 编号为 $m$。单位长度的运输费用为 1。航线是双向的。

再接下来一行是一个整数 $d$，后面的 $d$ 行每行是三个整数 $P(1<P<m),a,b(1\le a\le b\le n)$。表示编号为 $P$ 的码头从第 $a$ 天到第 $b$ 天无法装卸货物（含头尾）。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头 $A$ 到码头 $B$ 的运输路线。

【输出格式】

包括了一个整数表示最小的总成本。总成本 $=n$ 天运输路线长度之和 $+K\times $ 改变运输路线的次数。

【样例】

样例输入

5 5 10 8
1 2 1
1 3 3
1 4 2
2 3 2
2 4 4
3 4 1
3 5 2
4 5 2
4
2 2 3
3 1 1
3 3 3
4 4 5

样例输出

32

【样例解释】

上图依次表示第 $1$ 至第 $5$ 天的情况，阴影表示不可用的码头。

最优方案为：前三天走 $1\rightarrow 4\rightarrow 5$，后两天走 $1\rightarrow 3\rightarrow 5$，这样总成本为 $(2+2)\times 3+(3+2)\times 2+10=32$。

---

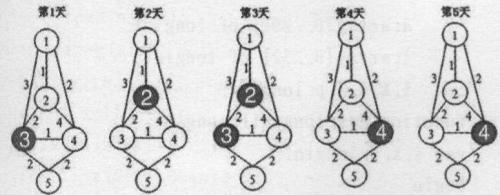
题解

【做题经理】

首先，这道题涉及最短路是肯定看得出来。

但是呢，到底该怎么处理有些路不能走的情况呢？

这个时候，我想到了最短路和次短路，用类似树 $dp$ 的办法对其进行处理。

但是这样想有个 $bug$ ，那就是万一最短路和次短路都走不通的情况呢？

然后我就开始疯狂幻想次次短路、次次次短路......

【正解】

我在考虑这道题的时候，忽略了这道题的数据范围：$n(1\le n\le 100),m(1\le m\le 20)$

可以看出 $n$ 和 $m$ 都是很小的，那么我们为什么不直接暴力做呢。

但是这个暴力也是基于 $dp$ 的基础上的。

首先可以设一个简单的状态：

$dp[i]$：到第 $i$ 天所用的最小花费

那么状转呼之而出

$dp[i]=dp[j]+cost[j+1][i]*(i-j)+K$

其中， $j$ 是我们改变航道的那天。此状转的意思就是从第 $j$ 天开始更换新的航道，由第 $j+1$ 天到第 $i$ 天用同一个航道，前 $j$ 天怎么走的不管，因为这是前面处理的事情，对于我们现阶段不影响。

那么现在只剩一个问题：$cost[i][j]$ 怎么求呢？

从定义入手：

$cost[i][j]$：从第 $i$ 天到第 $j$ 天用同一条航道的最小花费。

再回到前面所说的，此题数据范围很小，那么我们可以直接暴力处理出 $cost[i][j]$

那么代码也就出来了

#include<bits/stdc++.h>
using namespace std;
#define int long long
template<class T>inline void qread(T& x){
    char c;bool f=false;x=0;
    while((c=getchar())<'0'||'9'<c)if(c=='-')f=true;
    for(x=(c^48);'0'<=(c=getchar())&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    if(f)x=-x;
}
template<class T,class... Args>inline void qread(T& x,Args&... args){qread(x),qread(args...);}
inline int rqread(){
    char c;bool f=false;int x=0;
    while((c=getchar())<'0'||'9'<c)if(c=='-')f=true;
    for(x=(c^48);'0'<=(c=getchar())&&c<='9';x=(x<<1)+(x<<3)+(c^48));
    return f?-x:x;
}
template<class T>inline T Max(const T x,const T y){return x>y?x:y;}
template<class T>inline T Min(const T x,const T y){return x<y?x:y;}
template<class T>inline T fab(const T x){return x>0?x:-x;}
const int MAXN=100;
const int MAXM=20;
class gragh{
    #define EDGE_SIZE 400
    #define NODE_SIZE 20
    #define INF 0x3f3f3f3f
public:
    int N,M;
    struct edge{int to,nxt,w;
        edge(){}
        edge(const int T,const int Nx,const int W):to(T),nxt(Nx),w(W){}
    }e[EDGE_SIZE+5];
    int tail[NODE_SIZE+5],ind;
    inline void add_edge(const int u,const int to,const int w){e[++ind]=edge(to,tail[u],w);tail[u]=ind;}
    inline void dijkstra(int dis[],const int s,bool vis[]){
        struct node{int u,w;
            node(){}
            node(const int U,const int W):u(U),w(W){}
            bool operator<(const node a)const{return !(w<a.w);}
        };
        for(int i=1;i<=N;++i)dis[i]=INF;
        priority_queue<node>Q;
        Q.push(node(s,dis[s]=0));
        while(!Q.empty()){
            int u=Q.top().u;Q.pop();
            for(int i=tail[u],v;i;i=e[i].nxt)if(dis[v=e[i].to]>dis[u]+e[i].w&&!vis[v])
                Q.push(node(v,(dis[v]=dis[u]+e[i].w)));
        }
    }
    inline bool spfa(int dis[],const int s,bool vis[]){
        int cnt[NODE_SIZE+5];/*bool vis[EDGE_SIZE+5];*/
        queue<int>Q;
        for(int i=1;i<=N;++i)dis[i]=INF/*,vis[i]=false*/,cnt[i]=0;
        Q.push(s);
        dis[s]=0,cnt[s]=1;
        while(!Q.empty()){
            int now=Q.front();Q.pop();
            vis[now]=false,++cnt[now];
            if(cnt[now]>N)return false;
            for(int i=tail[now],v;i;i=e[i].nxt){
                v=e[i].to;
                if(dis[now]+e[i].w<dis[v]){
                    dis[v]=dis[now]+e[i].w;
                    if(!vis[v])Q.push(v),vis[v]=true;
                }
            }
        }
        return true;
    }
    inline void clr(){memset(tail,ind=0,sizeof tail);}
    gragh(){clr();}
    #undef EDGE_SIZE
    #undef NODE_SIZE
    #undef INF
}G;
int n,K,d,cost[MAXN+5][MAXN+5];
bool inf[MAXM+5][MAXN+5];
inline void init(){
    qread(n,G.N,K,G.M);
    for(int i=1,a,b,c;i<=G.M;++i){
        qread(a,b,c);
        G.add_edge(a,b,c);
        G.add_edge(b,a,c);
    }
    qread(d);
    for(int i=1,P,a,b;i<=d;++i){
        qread(P,a,b);
        for(int j=a;j<=b;++j)inf[P][j]=true;
    }
}
void calcCost(){
    bool vis[MAXM+5];int dis[MAXM+5];
    for(int i=1;i<=n;++i)for(int j=i;j<=n;++j){
        memset(vis,0,sizeof vis);
        for(int k=1;k<=G.N;++k)for(int t=i;t<=j;++t)
            if(inf[k][t]){vis[k]=true;break;}
        G.spfa(dis,1,vis);
        cost[i][j]=dis[G.N];
    }
}
inline void getDp(){
    int dp[MAXN+5];
    for(int i=1;i<=n;++i)dp[i]=0x3f3f3f3f;
    for(int i=1;i<=n;++i){
        dp[i]=cost[1][i]*i;
        for(int j=i-1;j>=0;--j)
            dp[i]=Min(dp[i],dp[j]+cost[j+1][i]*(i-j)+K);
    }
    printf("%lld\n",dp[n]);
}
signed main(){
    init();
    calcCost();
    getDp();
    return 0;
}