sklearn调用逻辑回归算法

1、逻辑回归算法即可以看做是回归算法，也可以看作是分类算法，通常用来解决分类问题，主要是二分类问题，对于多分类问题并不适合，也可以通过一定的技巧变形来间接解决。

2、决策边界是指不同分类结果之间的边界线(或者边界实体)，它具体的表现形式一定程度上说明了算法训练模型的过拟合程度，我们可以通过决策边界来调整算法的超参数。

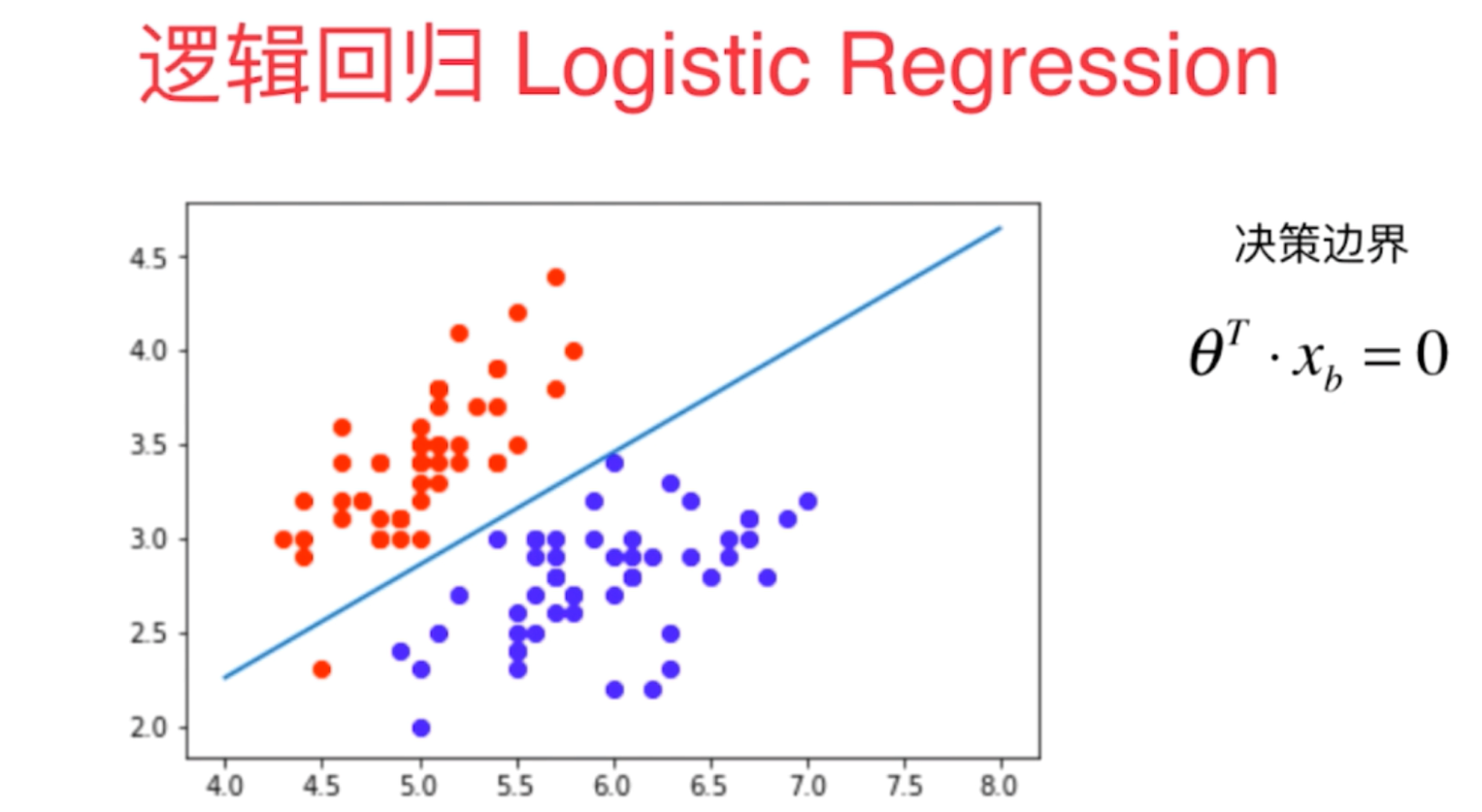
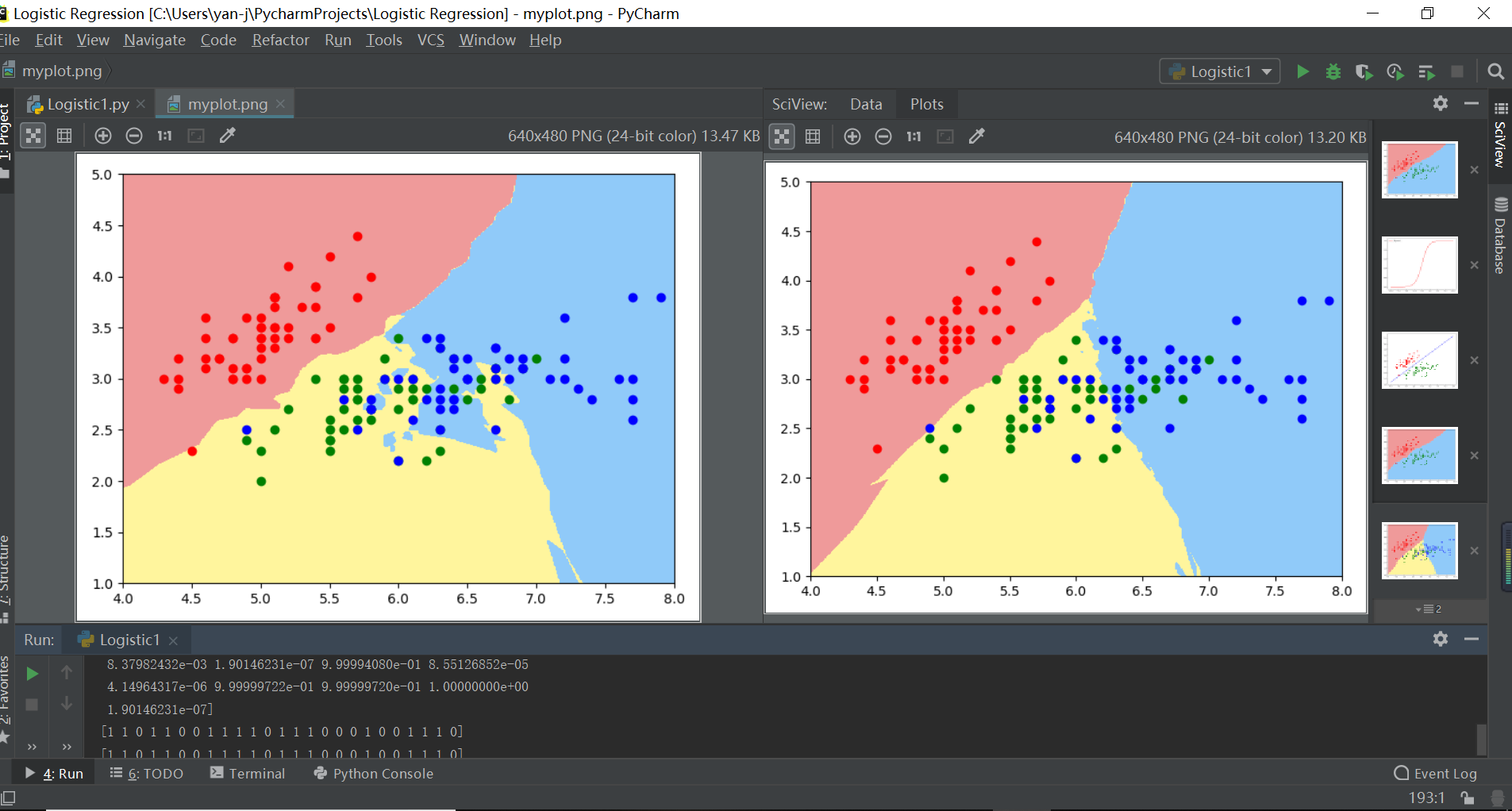
注解：左边逻辑回归拟合决策边界嘈杂冗余说明过拟合，右边决策边界分层清晰说明拟合度好

3、在逻辑回归中随着算法的复杂度不断地提高，其算法的过拟合也会越来越严重，为了避免这个现象，我们在逻辑回归中也需要进行正则化，以减小整体拟合的均方差，减少训练的过拟合现象。因此sklearn中调用逻辑回归时含有三个重要的超参数degree(多项式的最高次数)，C（正则化系数）以及penalty（正则化的方式l1/l2）

4、sklearn中逻辑回归使用的正则化方式如下：

import  numpy as np
import matplotlib.pyplot as plt
#定义概率转换函数sigmoid函数
def sigmoid(t):
    return 1/(1+np.exp(-t))
x=np.linspace(-10,10,100)
y=sigmoid(x)
plt.figure()
plt.plot(x,y,"r",label="Sigmoid")
plt.legend(loc=2)
plt.show()

from sklearn import datasets
d=datasets.load_iris()
x=d.data
y=d.target
x=x[y<2,:2]
y=y[y<2]

#定义机器学习算法的决策边界输出函数
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1,1)
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_pre=model.predict(x_new)
    zz=y_pre.reshape(x0.shape)
    from matplotlib.colors import ListedColormap
    cus=ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])
    plt.contourf(x0,x1,zz,cmap=cus)

from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)

from sklearn.neighbors import KNeighborsClassifier
knn1=KNeighborsClassifier()
knn1.fit(x_train,y_train)
plot_decision_boundary(knn1,axis=[4,8,1,5])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
knn2=KNeighborsClassifier(n_neighbors=50)  #k越大，模型越简单，也意味着过拟合的程度越轻，决策边界越清晰
knn2.fit(d.data[:,:2],d.target)
x=d.data
y=d.target
plot_decision_boundary(knn2,axis=[4,8,1,5])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.scatter(x[y==2,0],x[y==2,1],color="b")
plt.show()

#逻辑回归添加多项式回归
import numpy as np
import matplotlib.pyplot as plt
np.random.seed=666
x=np.random.normal(0,1,size=(100,2))
y=np.array(x[:,0]**2+x[:,1]**2<1.5,dtype="int")
knn2=KNeighborsClassifier() 
knn2.fit(x,y)
plot_decision_boundary(knn2,axis=[-4,4,-3,3])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()

### sklearn中调用逻辑回归算法函数
import numpy as np
import matplotlib.pyplot as plt
np.random.seed=666
x=np.random.normal(0,1,size=(200,2))
y=np.array(x[:,0]**2+x[:,1]<1.5,dtype="int")
for _ in range(20):
    y[np.random.randint(200)]=1
plt.figure()
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#1-1单纯的逻辑回归算法
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
from sklearn.linear_model import LogisticRegression
log=LogisticRegression()
log.fit(x_train,y_train)
print(log.score(x_test,y_test))
knn3=KNeighborsClassifier()
knn3.fit(x_train,y_train)
print(knn3.score(x_test,y_test))
#1-2sklearn中的逻辑回归（多项式参与，并不带正则化）
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def polynomiallogisticregression(degree):
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_reg",StandardScaler()),
        ("log_reg",LogisticRegression())
    ])
x=np.random.normal(0,1,size=(200,2))
y=np.array(x[:,0]**2+x[:,1]<1.5,dtype="int")
for _ in range(20):
    y[np.random.randint(200)]=1
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)
p1=polynomiallogisticregression(degree=2)
p1.fit(x_train,y_train)
print(p1.score(x_train,y_train))
print(p1.score(x_test,y_test))
plot_decision_boundary(p1,axis=[-4,4,-4,4])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
p1=polynomiallogisticregression(degree=20)  #当其次数变为高次时，其训练模型已经过拟合
p1.fit(x_train,y_train)
print(p1.score(x_train,y_train))
print(p1.score(x_test,y_test))
plot_decision_boundary(p1,axis=[-4,4,-4,4])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()
#1-3逻辑回归的正则化形式函数
def Polynomiallogisticregression(degree,C,penalty):   #逻辑回归的三大超参数
    return Pipeline([
        ("poly",PolynomialFeatures(degree=degree)),
        ("std_reg",StandardScaler()),
        ("log_reg",LogisticRegression(C=C,penalty=penalty))
    ])
p1=Polynomiallogisticregression(degree=20,C=1,penalty="l2")  #当其次数变为高次时，其训练模型已经过拟合
p1.fit(x_train,y_train)
print(p1.score(x_train,y_train))
print(p1.score(x_test,y_test))
plot_decision_boundary(p1,axis=[-4,4,-4,4])
plt.scatter(x[y==0,0],x[y==0,1],color="r")
plt.scatter(x[y==1,0],x[y==1,1],color="g")
plt.show()

其输出结果对比如下所示：

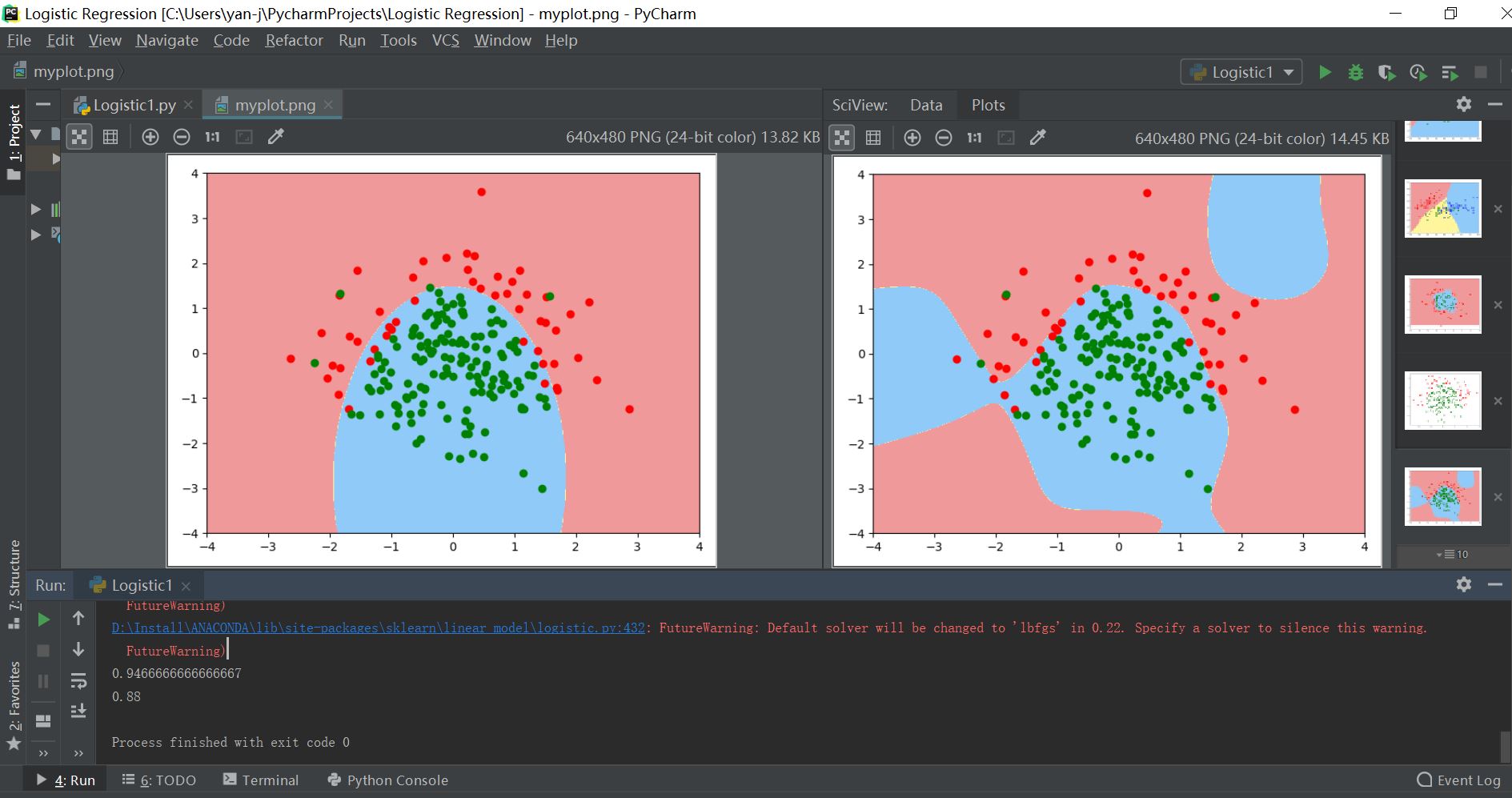
               注：左为拟合度比较好的决策边界，右边为高次的过拟合训练模型