51nod 1488 帕斯卡小三角 斜率优化

思路：斜率优化

提交：\(2\)次

错因：二分写挂

题解：

首先观察可知，



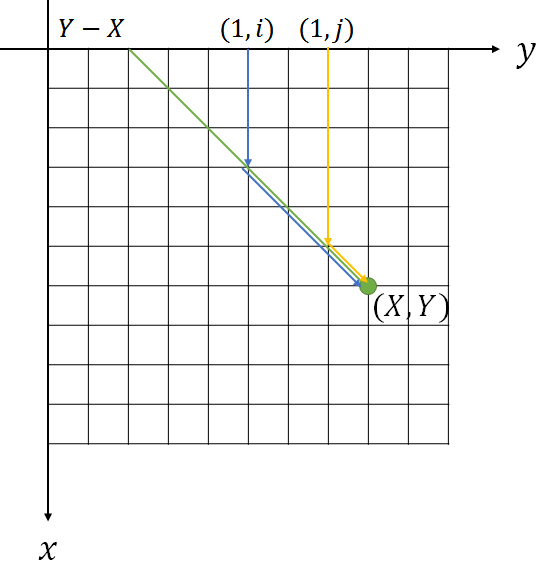
对于点\(f(X,Y)\)，一定是由某个点\((1,p)\)，先向下走，再向右下走。

并且有个显然的性质，若从\((1,p)\)向下走，则\(a[p]=min(a[i]),i\in [p,Y]\)（要不然直接从后面的更小的那个位置向下走，再向右下走）

还有一个显然的性质，若\(i<j\)且\(i\)比\(j\)更优，则\(a[i]>a[j]\)(上面的结论)

设\(s[i]=\sum_{j=i}^i a[j]\)

那么对于点\(f(X,Y)\)有\(ans=s[Y]-s[i]+a[i]*(X-Y+i),i\in [max(1,Y-X),Y]\)

这个式子是可以斜率优化的：\(s[i]-a[i]*i=(X-Y)*a[i]+s[Y]-ans\)

要最小化\(ans\)，就是最大化\(s[Y]-ans\)，所以我们用单调栈维护下降斜率（上凸包），每次先查找合法区间\(i\in [max(1,Y-X),Y]\),然后再在单调栈中二分斜率。

#include<cstdio>
#include<iostream>
#include<algorithm>
#define R register int
using namespace std;
namespace Luitaryi {
template<class I> inline I g(I& x) { x=0;
  register I f=1; register char ch; while(!isdigit(ch=getchar())) f=ch=='-'?-1:f;
  do x=x*10+(ch^48); while(isdigit(ch=getchar())); return x*=f;
} const int N=1e5+10;
int n,m,a[N],s[N],stk[N],ans[N],t;
struct node {int x,y,p;
  inline bool operator < (const node& that) const {return y<that.y;}
}b[N];
inline int getlim(int pos) {
  R l=1,r=t; while(l<r) { R md=l+r>>1;
    if(stk[md]<pos) l=md+1; else r=md;
  } return l;
}
inline double calc(int i,int j) {return ((double)(s[i]-a[i]*i)-(double)(s[j]-a[j]*j))/(double)(a[i]-a[j]);}
inline void main() {
  g(n); for(R i=1;i<=n;++i) g(a[i]),s[i]=s[i-1]+a[i];
  g(m); for(R i=1;i<=m;++i) g(b[i].x),g(b[i].y),b[i].p=i;
  sort(b+1,b+m+1); for(R i=1,j=1;i<=n;++i) {
    while(t&&a[stk[t]]>=a[i]) --t;
    while(t>1&&calc(stk[t],i)>=calc(stk[t-1],i)) --t;
    stk[++t]=i; while(b[j].y==i&&j<=m) {
      R l=getlim(b[j].y-b[j].x),r=t;
      while(l<r) { R md=l+r>>1;
        if(calc(stk[md],stk[md+1])<b[j].x-b[j].y) r=md;
        else l=md+1;
      } l=stk[l],r=b[j].y;
      ans[b[j].p]=s[r]-s[l]+a[l]*(b[j].x-r+l); ++j;
    }
  } for(R i=1;i<=m;++i) printf("%d\n",ans[i]);
}
} signed main() {Luitaryi::main(); return 0;}

2019.08.12

88