CNN-2: AlexNet 卷积神经网络模型
1、AlexNet 模型简介
由于受到计算机性能的影响,虽然LeNet在图像分类中取得了较好的成绩,但是并没有引起很多的关注。 知道2012年,Alex等人提出的AlexNet网络在ImageNet大赛上以远超第二名的成绩夺冠,卷积神经网络乃至深度学习重新引起了广泛的关注。
2、AlexNet 模型特点
AlexNet是在LeNet的基础上加深了网络的结构,学习更丰富更高维的图像特征。AlexNet的特点:
1)更深的网络结构
2)使用层叠的卷积层,即卷积层+卷积层+池化层来提取图像的特征
3)使用Dropout抑制过拟合
4)使用数据增强Data Augmentation抑制过拟合
5)使用Relu替换之前的sigmoid的作为激活函数
6)多GPU训练
ReLu作为激活函数
在最初的感知机模型中,输入和输出的关系如下:
${y = \sum\limits_i {{w_i}{x_i}} + b}$
只是单纯的线性关系,这样的网络结构有很大的局限性:即使用很多这样结构的网络层叠加,其输出和输入仍然是线性关系,无法处理有非线性关系的输入输出。因此,对每个神经元的输出做个非线性的转换也就是,将上面就加权求和${\sum\nolimits_i {{w_i}{x_i}} + b}$的结果输入到一个非线性函数,也就是激活函数中。 这样,由于激活函数的引入,多个网络层的叠加就不再是单纯的线性变换,而是具有更强的表现能力。

在最初,sigmoid和tanh函数最常用的激活函数。
1) sigmoid
${\sigma \left( x \right) = \frac{1}{{1 + {e^{ - x}}}}}$
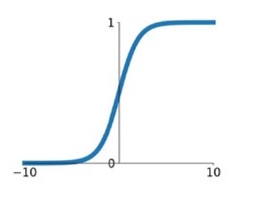
在网络层数较少时,sigmoid函数的特性能够很好的满足激活函数的作用:它把一个实数压缩至0到1之间,当输入的数字非常大的时候,结果会接近1;当输入非常大的负数时,则会得到接近0的结果。这种特性,能够很好的模拟神经元在受刺激后,是否被激活向后传递信息(输出为0,几乎不被激活;输出为1,完全被激活)。
sigmoid一个很大的问题就是梯度饱和。 观察sigmoid函数的曲线,当输入的数字较大(或较小)时,其函数值趋于不变,其导数变的非常的小。这样,在层数很多的的网络结构中,进行反向传播时,由于很多个很小的sigmoid导数累成,导致其结果趋于0,权值更新较慢。
2) ReLu
${ReLU\left( x \right) = max\left( {0\user1{,}x} \right)}$
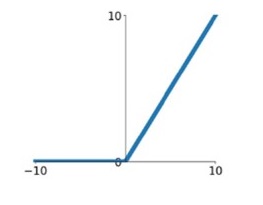
针对sigmoid梯度饱和导致训练收敛慢的问题,在AlexNet中引入了ReLU。ReLU是一个分段线性函数,小于等于0则输出为0;大于0的则恒等输出。相比于sigmoid,ReLU有以下有点:
1)计算开销下。sigmoid的正向传播有指数运算,倒数运算,而ReLu是线性输出;反向传播中,sigmoid有指数运算,而ReLU有输出的部分,导数始终为1.
2)梯度饱和问题
3)稀疏性。Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
这里有个问题,前面提到,激活函数要用非线性的,是为了使网络结构有更强的表达的能力。那这里使用ReLU本质上却是个线性的分段函数,是怎么进行非线性变换的。 这里把神经网络看着一个巨大的变换矩阵M,其输入为所有训练样本组成的矩阵A,输出为矩阵B。
${B = M \cdot A}$
这里的M是一个线性变换的话,则所有的训练样本A进行了线性变换输出为B。 那么对于ReLU来说,由于其是分段的,0的部分可以看着神经元没有激活,不同的神经元激活或者不激活,其神经玩过组成的变换矩阵是不一样的。也就是说,每个训练样本使用的线性变换矩阵是不一样的,在整个训练样本空间来说,其经历的是非线性变换。
简单来说,不同训练样本中的同样的特征,在经过神经网络学习时,流经的神经元是不一样的(激活函数值为0的神经元不会被激活)。这样,最终的输出实际上是输入样本的非线性变换。单个训练样本是线性变换,但是每个训练样本的线性变换是不一样的,这样整个训练样本集来说,就是非线性的变换。
数据增强
神经网络由于训练的参数多,表能能力强,所以需要比较多的数据量,不然很容易过拟合。当训练数据有限时,可以通过一些变换从已有的训练数据集中生成一些新的数据,以快速地扩充训练数据。对于图像数据集来说,可以对图像进行一些形变操作:
1) 翻转
2) 随机裁剪
3)平移,颜色光照的变换
...
AlexNet中对数据做了以下操作:
1)随机裁剪,对256×256的图片进行随机裁剪到227×227,然后进行水平翻转。
2)测试的时候,对左上、右上、左下、右下、中间分别做了5次裁剪,然后翻转,共10个裁剪,之后对结果求平均。
3)对RGB空间做PCA(主成分分析),然后对主成分做一个(0, 0.1)的高斯扰动,也就是对颜色、光照作变换,结果使错误率又下降了1%。
层叠池化
在LeNet中池化是不重叠的,即池化的窗口的大小和步长是相等的,如下:

在AlexNet中使用的池化(Pooling)却是可重叠的,也就是说,在池化的时候,每次移动的步长小于池化的窗口长度。AlexNet池化的大小为3×3的正方形,每次池化移动步长为2,这样就会出现重叠。重叠池化可以避免过拟合,这个策略贡献了0.3%的Top-5错误率。与非重叠方案s=2,z=2相比,输出的维度是相等的,并且能在一定程度上抑制过拟合。
局部相应归一化
ReLU具有让人满意的特性,它不需要通过输入归一化来防止饱和。如果至少一些训练样本对ReLU产生了正输入,那么那个神经元上将发生学习。然而,我们仍然发现接下来的局部响应归一化有助于泛化。${a_{x{,}y}^i}$表示神经元激活,通过在(x,y)(位置应用核${i}$然后应用ReLU非线性来计算,响应归一化激活${b_{x{,}y}^i}$通过下式给定:
${b_{x{,}y}^i = \frac{{a_{x{,}y}^i}}{{{{\left( {k + \alpha \sum\limits_{j = {max}\left( {{0,}{{{i - n}} \mathord{\left/
{\vphantom {{{i - n}} 2}} \right.
\kern-\nulldelimiterspace} 2}} \right)}^{{min(N - 1,}{{{i + n}} \mathord{\left/
{\vphantom {{{i + n}} 2}} \right.
\kern-\nulldelimiterspace} 2}{)}} {{{\left( {a_{x{,}y}^j} \right)}^2}} } \right)}^\beta }}}}$
其中,N是卷积核的个数,也就是生成的FeatureMap的个数;${k{,}\alpha {,}\beta {,}n}$是超参数,论文中使用的值是${k = 2{,}\alpha = {10^{ - 4}}{,}\beta = 0.75{,}n = 5}$。输出${b_{x{,}y}^i}$和输入${a_{x{,}y}^i}$的上标表示的是当前值所在的通道,也即是叠加的方向是沿着通道进行。将要归一化的值${a_{x{,}y}^i}$所在附近通道相同位置的值的平方累加起来${\sum\nolimits_{j = {max}\left( {{0,}{{{i - n}} \mathord{\left/
{\vphantom {{{i - n}} 2}} \right.
\kern-\nulldelimiterspace} 2}} \right)}^{{min(N - 1,}{{{i + n}} \mathord{\left/
{\vphantom {{{i + n}} 2}} \right.
\kern-\nulldelimiterspace} 2}{)}} {{{\left( {a_{x{,}y}^j} \right)}^2}} }$
Dropout
这个是比较常用的抑制过拟合的方法了。 引入Dropout主要是为了防止过拟合。在神经网络中Dropout通过修改神经网络本身结构来实现,对于某一层的神经元,通过定义的概率将神经元置为0,这个神经元就不参与前向和后向传播,就如同在网络中被删除了一样,同时保持输入层与输出层神经元的个数不变,然后按照神经网络的学习方法进行参数更新。在下一次迭代中,又重新随机删除一些神经元(置为0),直至训练结束。 Dropout应该算是AlexNet中一个很大的创新,现在神经网络中的必备结构之一。Dropout也可以看成是一种模型组合,每次生成的网络结构都不一样,通过组合多个模型的方式能够有效地减少过拟合,Dropout只需要两倍的训练时间即可实现模型组合(类似取平均)的效果,非常高效。 如下图:
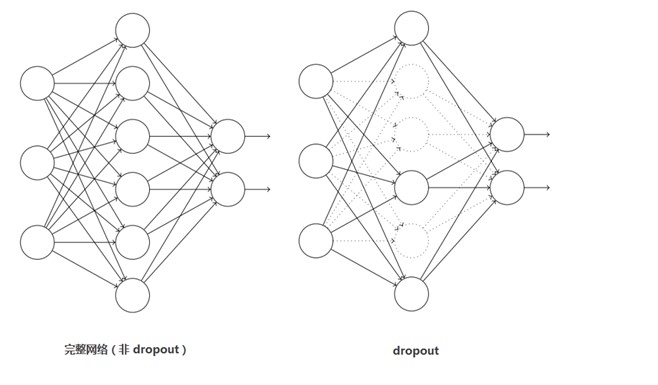
3、Alex网络结构
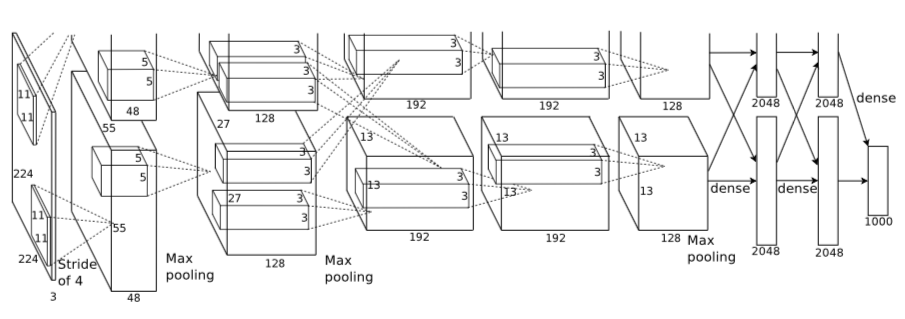
注:上图中的输入是224×224,不过经过计算(224−11)/4=54.75并不是论文中的55×55,而使用227×227作为输入,则(227−11)/4=55。
网络包含8个带权重的层;前5层是卷积层,剩下的3层是全连接层。最后一层全连接层的输出是1000维softmax的输入,softmax会产生1000类标签的分布网络包含8个带权重的层;前5层是卷积层,剩下的3层是全连接层。最后一层全连接层的输出是1000维softmax的输入,softmax会产生1000类标签的分布。
- 卷积层C1
该层的处理流程是: 卷积-->ReLU-->池化-->归一化。
1)卷积,输入是227×227,使用96个11×11×3的卷积核,得到的FeatureMap为55×55×96。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
3)池化,使用3×3步长为2的池化单元(重叠池化,步长小于池化单元的宽度),输出为27×27×96((55−3)/2+1=27)。
4)局部响应归一化,使用k=2,n=5,α=10−4,β=0.75进行局部归一化,输出的仍然为27×27×96,输出分为两组,每组的大小为27×27×48。
- 卷积层C2
该层的处理流程是:卷积-->ReLU-->池化-->归一化。
1)卷积,输入是2组27×27×48。使用2组,每组128个尺寸为5×5×48的卷积核,并作了边缘填充padding=2,卷积的步长为1. 则输出的FeatureMap为2组,每组的大小为 27×27 times128. ((27+2∗2−5)/1+1=27)。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
3)池化运算的尺寸为3×3,步长为2,池化后图像的尺寸为(27−3)/2+1=13,输出为13×13×256。
4)局部响应归一化,使用k=2,n=5,α=10−4,β=0.75进行局部归一化,输出的仍然为13×13×256,输出分为2组,每组的大小为13×13×128。
- 卷积层C3
该层的处理流程是: 卷积-->ReLU。
1)卷积,输入是13×13×256,使用2组共384尺寸为3×3×256的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13 times384。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
- 卷积层C4
该层的处理流程是: 卷积-->ReLU
该层和C3类似。
1)卷积,输入是13×13×384,分为两组,每组为13×13×192.使用2组,每组192个尺寸为3×3×192的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13 times384,分为两组,每组为13×13×192。
2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
- 卷积层C5
该层处理流程为:卷积-->ReLU-->池化
卷积,输入为13×13×384,分为两组,每组为13×13×192。使用2组,每组为128尺寸为3×3×192的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13×256。
ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
池化,池化运算的尺寸为3×3,步长为2,池化后图像的尺寸为 (13−3)/2+1=6,即池化后的输出为6×6×256。
- 全连接层FC6
该层的流程为:(卷积)全连接 -->ReLU -->Dropout
1)卷积->全连接: 输入为6×6×256,该层有4096个卷积核,每个卷积核的大小为6×6×256。由于卷积核的尺寸刚好与待处理特征图(输入)的尺寸相同,即卷积核中的每个系数只与特征图(输入)尺寸的一个像素值相乘,一一对应,因此,该层被称为全连接层。由于卷积核与特征图的尺寸相同,卷积运算后只有一个值,因此,卷积后的像素层尺寸为4096×1×1,即有4096个神经元。
2)ReLU,这4096个运算结果通过ReLU激活函数生成4096个值
3)Dropout,抑制过拟合,随机的断开某些神经元的连接或者是不激活某些神经元。
- 全连接层FC7
流程为:全连接-->ReLU-->Dropout
1)全连接,输入为4096的向量。
2)ReLU,这4096个运算结果通过ReLU激活函数生成4096个值。
3)Dropout,抑制过拟合,随机的断开某些神经元的连接或者是不激活某些神经元。
- 输出层
第七层输出的4096个数据与第八层的1000个神经元进行全连接,经过训练后输出1000个float型的值,这就是预测结果。
4)AlexNet参数数量
卷积层的参数 = 卷积核的数量 * 卷积核 + 偏置
C1: 96个11×11×3的卷积核,96×11×11×3+96=34848
C2: 2组,每组128个5×5×48的卷积核,(128×5×5×48+128)×2=307456
C3: 384个3×3×256的卷积核,3×3×256×384+384=885120
C4: 2组,每组192个3×3×192的卷积核,(3×3×192×192+192)×2=663936
C5: 2组,每组128个3×3×192的卷积核,(3×3×192×128+128)×2=442624
FC6: 4096个6×6×256的卷积核,6×6×256×4096+4096=37752832
FC7: 4096∗4096+4096=16781312
output: 4096∗1000=4096000
卷积层 C2,C4,C5中的卷积核只和位于同一GPU的上一层的FeatureMap相连。从上面可以看出,参数大多数集中在全连接层,在卷积层由于权值共享,权值参数较少。
5)AlexNet模型TensorFlow实现
开发环境: Python - 3.0、TensorFlow - 1.4.0、无GPU
- # -*- coding: utf-8 -*-
- """
- Created on 2017
- @author: 黄文坚、唐源
- """
- # 6.1 TensorFlow 实现 AlexNet
- # 2012年 Hinton 的学生 ALex Krizhevsky 提出
- # 为 LeNet的一种更深更宽的版本
- # 首次在CNN 中成功应用了 ReLU激活函数解决Sigmoid在网络较深时的梯度弥散问题、
- # Dropout 随机忽略一部分神经元,以避免模型过拟合(全连接层使用)
- # 使用重叠的最大池化,且步长比池化核的尺寸小,此前普遍使用的是平均池化,避免平均池化的模糊化效果
- # 提出LRN层对局部神经元的活动创建竞争机制,增强模型泛化能力
- # 使用 GPU 进行运算加速、增强数据
- # 5个卷积层、其中3个卷积层后连接了最大池化层,最后还有3个全连接层
- from datetime import datetime
- import math
- import time
- import tensorflow as tf
- batch_size=32
- num_batches=100
- def print_activations(t):
- print(t.op.name, ' ', t.get_shape().as_list())
- def inference(images):
- parameters = []
- # conv1
- with tf.name_scope('conv1') as scope:
- #定义卷积层参数:前两个为尺寸 11*11(标准差0.1)、第三个为当前层节点矩阵的深度 3、第四个为卷积层的深度 64
- kernel = tf.Variable(tf.truncated_normal([11, 11, 3, 64], dtype=tf.float32,
- stddev=1e-1), name='weights')
- #tf.nn.conv2d 提供了一个方便的卷积层前向传播函数
- #参数1:当前层的节点矩阵,四维矩阵,第一维度对应一个输入batch,如第一张图片,第二张图片..
- #参数2:卷积层参数
- #参数3:不同维度上的步长(第一维、最后一维必须为1)
- #参数4:提供'SAME'和'VALLD'选择,'SAME'为添加全0填充,'VALLD'为不添加
- conv = tf.nn.conv2d(images, kernel, [1, 4, 4, 1], padding='SAME')
- #定义偏置项为 1,及下一层节点矩阵的深度 1(参数共享)
- biases = tf.Variable(tf.constant(0.0, shape=[64], dtype=tf.float32),
- trainable=True, name='biases')
- #tf.nn.bias_add提供给每个conv节点加上偏置项
- bias = tf.nn.bias_add(conv, biases)
- #将计算结果通过ReLU激活函数完成去线性化
- conv1 = tf.nn.relu(bias, name=scope)
- print_activations(conv1)
- parameters += [kernel, biases]
- # pool1
- lrn1 = tf.nn.lrn(conv1, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75, name='lrn1')
- #tf.nn.max_pool 提供了一个方便的最大池化层的前向传播过程。
- #tf.nn.avg_pool 提供了一个方便的平均池化层的前向传播过程,两者参数一致。
- #参数1:四维矩阵,第一维度对应一个输入batch,如第一张图片,第二张图片.
- #参数2:ksize为过滤器参数,常为[1, 2, 2, 1]、[1, 3, 3, 1]
- #参数3:不同维度上的步长(第一维、最后一维必须为1)
- #参数4:提供'SAME'和'VALLD'选择,'SAME'为添加全0填充,'VALLD'为不添加
- pool1 = tf.nn.max_pool(lrn1,
- ksize=[1, 3, 3, 1],
- strides=[1, 2, 2, 1],
- padding='VALID',
- name='pool1')
- print_activations(pool1)
- # conv2
- with tf.name_scope('conv2') as scope:
- kernel = tf.Variable(tf.truncated_normal([5, 5, 64, 192], dtype=tf.float32,
- stddev=1e-1), name='weights')
- conv = tf.nn.conv2d(pool1, kernel, [1, 1, 1, 1], padding='SAME')
- biases = tf.Variable(tf.constant(0.0, shape=[192], dtype=tf.float32),
- trainable=True, name='biases')
- bias = tf.nn.bias_add(conv, biases)
- conv2 = tf.nn.relu(bias, name=scope)
- parameters += [kernel, biases]
- print_activations(conv2)
- # pool2
- lrn2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75, name='lrn2')
- pool2 = tf.nn.max_pool(lrn2,
- ksize=[1, 3, 3, 1],
- strides=[1, 2, 2, 1],
- padding='VALID',
- name='pool2')
- print_activations(pool2)
- # conv3
- with tf.name_scope('conv3') as scope:
- kernel = tf.Variable(tf.truncated_normal([3, 3, 192, 384],
- dtype=tf.float32,
- stddev=1e-1), name='weights')
- conv = tf.nn.conv2d(pool2, kernel, [1, 1, 1, 1], padding='SAME')
- biases = tf.Variable(tf.constant(0.0, shape=[384], dtype=tf.float32),
- trainable=True, name='biases')
- bias = tf.nn.bias_add(conv, biases)
- conv3 = tf.nn.relu(bias, name=scope)
- parameters += [kernel, biases]
- print_activations(conv3)
- # conv4
- with tf.name_scope('conv4') as scope:
- kernel = tf.Variable(tf.truncated_normal([3, 3, 384, 256],
- dtype=tf.float32,
- stddev=1e-1), name='weights')
- conv = tf.nn.conv2d(conv3, kernel, [1, 1, 1, 1], padding='SAME')
- biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32),
- trainable=True, name='biases')
- bias = tf.nn.bias_add(conv, biases)
- conv4 = tf.nn.relu(bias, name=scope)
- parameters += [kernel, biases]
- print_activations(conv4)
- # conv5
- with tf.name_scope('conv5') as scope:
- kernel = tf.Variable(tf.truncated_normal([3, 3, 256, 256],
- dtype=tf.float32,
- stddev=1e-1), name='weights')
- conv = tf.nn.conv2d(conv4, kernel, [1, 1, 1, 1], padding='SAME')
- biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32),
- trainable=True, name='biases')
- bias = tf.nn.bias_add(conv, biases)
- conv5 = tf.nn.relu(bias, name=scope)
- parameters += [kernel, biases]
- print_activations(conv5)
- # pool5
- pool5 = tf.nn.max_pool(conv5,
- ksize=[1, 3, 3, 1],
- strides=[1, 2, 2, 1],
- padding='VALID',
- name='pool5')
- print_activations(pool5)
- return pool5, parameters
- def time_tensorflow_run(session, target, info_string):
- # """Run the computation to obtain the target tensor and print timing stats.
- #
- # Args:
- # session: the TensorFlow session to run the computation under.
- # target: the target Tensor that is passed to the session's run() function.
- # info_string: a string summarizing this run, to be printed with the stats.
- #
- # Returns:
- # None
- # """
- num_steps_burn_in = 10
- total_duration = 0.0
- total_duration_squared = 0.0
- for i in range(num_batches + num_steps_burn_in):
- start_time = time.time()
- _ = session.run(target)
- duration = time.time() - start_time
- if i >= num_steps_burn_in:
- if not i % 10:
- print ('%s: step %d, duration = %.3f' %
- (datetime.now(), i - num_steps_burn_in, duration))
- total_duration += duration
- total_duration_squared += duration * duration
- mn = total_duration / num_batches
- vr = total_duration_squared / num_batches - mn * mn
- sd = math.sqrt(vr)
- print ('%s: %s across %d steps, %.3f +/- %.3f sec / batch' %
- (datetime.now(), info_string, num_batches, mn, sd)) #计算每轮迭代耗时的评测函数(平均耗时、标准差)
- def run_benchmark():
- # """Run the benchmark on AlexNet."""
- with tf.Graph().as_default():
- # Generate some dummy images.
- image_size = 224
- # Note that our padding definition is slightly different the cuda-convnet.
- # In order to force the model to start with the same activations sizes,
- # we add 3 to the image_size and employ VALID padding above.
- images = tf.Variable(tf.random_normal([batch_size, #使用随机图片数据
- image_size,
- image_size, 3],
- dtype=tf.float32,
- stddev=1e-1))
- # Build a Graph that computes the logits predictions from the
- # inference model.
- pool5, parameters = inference(images) #得到池化层的输出pool5和网络中需要训练的参数集合
- # Build an initialization operation.
- init = tf.global_variables_initializer()
- # Start running operations on the Graph.
- config = tf.ConfigProto()
- config.gpu_options.allocator_type = 'BFC'
- sess = tf.Session(config=config)
- sess.run(init)
- # Run the forward benchmark.
- time_tensorflow_run(sess, pool5, "Forward") #计算运行时间
- # Add a simple objective so we can calculate the backward pass.
- objective = tf.nn.l2_loss(pool5)
- # Compute the gradient with respect to all the parameters.
- grad = tf.gradients(objective, parameters)
- # Run the backward benchmark.
- time_tensorflow_run(sess, grad, "Forward-backward")
- if __name__ == "__main__":
- run_benchmark()
参考文献
[1] https://www.cnblogs.com/wangguchangqing/p/10333370.html
[2] Krizhevsky A , Sutskever I , Hinton G . ImageNet Classification with Deep Convolutional Neural Networks[C]// NIPS. Curran Associates Inc. 2012.
[3] 黄文坚、唐源等. TensorFlow 实战 [M] , 北京:电子工业出版社,2017.
CNN-2: AlexNet 卷积神经网络模型的更多相关文章
- 使用PyTorch简单实现卷积神经网络模型
这里我们会用 Python 实现三个简单的卷积神经网络模型:LeNet .AlexNet .VGGNet,首先我们需要了解三大基础数据集:MNIST 数据集.Cifar 数据集和 ImageNet 数 ...
- 利用Tensorflow实现卷积神经网络模型
首先看一下卷积神经网络模型,如下图: 卷积神经网络(CNN)由输入层.卷积层.激活函数.池化层.全连接层组成,即INPUT-CONV-RELU-POOL-FC池化层:为了减少运算量和数据维度而设置的一 ...
- 手写数字识别 ----卷积神经网络模型官方案例注释(基于Tensorflow,Python)
# 手写数字识别 ----卷积神经网络模型 import os import tensorflow as tf #部分注释来源于 # http://www.cnblogs.com/rgvb178/p/ ...
- CNN-1: LeNet-5 卷积神经网络模型
1.LeNet-5模型简介 LeNet-5 模型是 Yann LeCun 教授于 1998 年在论文 Gradient-based learning applied to document ...
- 【TensorFlow/简单网络】MNIST数据集-softmax、全连接神经网络,卷积神经网络模型
初学tensorflow,参考了以下几篇博客: soft模型 tensorflow构建全连接神经网络 tensorflow构建卷积神经网络 tensorflow构建卷积神经网络 tensorflow构 ...
- CNN-4: GoogLeNet 卷积神经网络模型
1.GoogLeNet 模型简介 GoogLeNet 是2014年Christian Szegedy提出的一种全新的深度学习结构,该模型获得了ImageNet挑战赛的冠军. 2.GoogLeNet 模 ...
- caffe中LetNet-5卷积神经网络模型文件lenet.prototxt理解
caffe在 .\examples\mnist文件夹下有一个 lenet.prototxt文件,这个文件定义了一个广义的LetNet-5模型,对这个模型文件逐段分解一下. name: "Le ...
- CNN-3: VGGNet 卷积神经网络模型
1.VGGNet 模型简介 VGG Net由牛津大学的视觉几何组(Visual Geometry Group)和 Google DeepMind公司的研究员一起研发的的深度卷积神经网络,在 ILSVR ...
- 吴裕雄--天生自然python Google深度学习框架:经典卷积神经网络模型
import tensorflow as tf INPUT_NODE = 784 OUTPUT_NODE = 10 IMAGE_SIZE = 28 NUM_CHANNELS = 1 NUM_LABEL ...
随机推荐
- Linux swap的创建与配置
在Linux下,swap的作用类似Windows系统下的“虚拟内存”.当物理内存不足时,拿出部分硬盘空间当SWAP分区(虚拟成内存)使用,从而解决内存容量不足的情况.Linux下的swap有两种实现形 ...
- wepy框架入门
安装 wepy 命令行工具. npm install wepy-cli -g 在开发目录生成开发DEMO. wepy new myproject 开发实时编译. wepy build --watch ...
- 控制层@Value注解取不到值
@Value("${enable-upload-image}") private String enable; 如上所示,同样的代码,写在在业务层,运行时能取到正确的值,但在控制层 ...
- Linux下java环境变量配置
安装步骤 1.查看当前Linux系统是否安装java rpm -qa | grep java 2.卸载系统中已经存在的openJDK rpm -e --nodeps java--openjdk-1.7 ...
- ansible 主机正则
ansible <pattern> -m <module_name> -a <arguments> 该功能主要针对Inventory的主机列表,案例如下: 1.AL ...
- 4)抽象方法不能为private,final或者static,为什么?
抽象方法的最实质的意 义在于被未来的子类覆盖实现掉.它自己是个空方法.private的实质意义在于本类其他方法调用它.你自己是个空方法,别人调用你有什么用?所以 abstract和private在一起 ...
- Spring —— @Async注解的使用
参考文档 Spring Boot使用@Async实现异步调用:自定义线程池 Spring Boot使用@Async实现异步调用:ThreadPoolTaskScheduler线程池的优雅关闭
- GDB使用——pwn相关
目录 寄存器 内存 peda插件命令 x命令详解 后续补充 内容来源 寄存器 1.查看寄存器 2.查看所有寄存器 3.查看某个寄存器 4.修改寄存器的值 内存 1.修改内存值 2.搜索内存 peda插 ...
- 什么是IO流
先看一段百度上的解释: 当然:如果你看不懂,那么你只需要记住下面3句话. 1. (1).我们知道,每个人家里喝的水都是从自来水厂来的,自来水厂的水又是从水源地来的, (2).水是通过水管来的. (3) ...
- Hibernate HQL和QBC
OID查询 一.什么是OID查询 根据对象的OID主键进行检索 二.OID查询方式 1. get方法 当get()方法被调用的时候就会立即发出SQL语句 并且返回的对象也是实际的对象 使用get()和 ...
