从二叉查找树到平衡树：avl, 2-3树，左倾红黑树（含实现代码），传统红黑树

参考：自平衡二叉查找树 ，红黑树， 算法：理解红黑树 （英文pdf：红黑树）

目录

• 自平衡二叉树介绍
• avl树
• 2-3树
• LLRBT(Left-leaning red-black tree左倾红黑树 （代码见git）
• 2-3-4树和红黑树
• avl和红黑树的比较

自平衡二叉查找树

诞生的目的：

它是为了解决二叉查找树的查找时间复杂度最差是O(n)的问题而发明的数据结构。

完全二叉树的公式： n = 2^h - 1

BST的查找运行时间和BST的高度有关。一个树的高度指的是从树的根开始所能到达的最长的路径长度。

如果按照从小到大的顺序输入一组key值，得到的将是一棵只有右子树的树。见下图。

如这个例子：

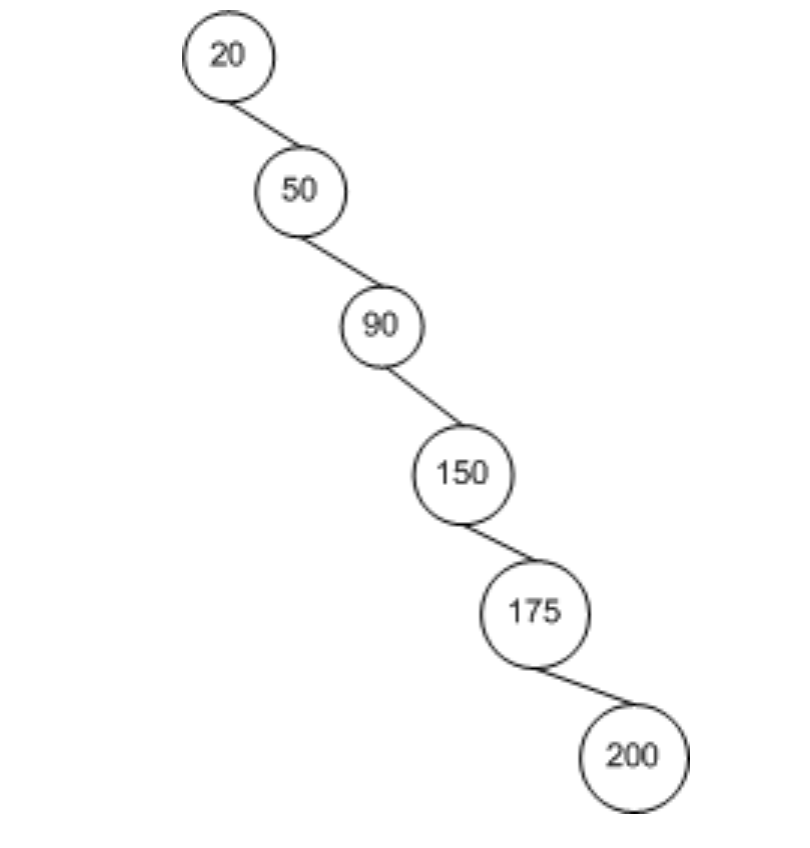
有6个节点，它的时间复杂度是O(n)。无论是新增，变更还是查找，删除，都需要诸葛对比key值。

假如要查找节点200，那么节点会比较5次，相当于遍历所有节点了。

这太浪费时间了，因此降低树的高度，就可以减少时间复杂度。

我们知道二叉搜索树的搜索节点的最小时间复杂度是 O(log­₂n)。因此找到一个高度和节点数量的最佳比例。让它的时间复杂度维持在O(log­₂n)。

期望是：

如果树中节点的数量为 n，则一棵满足O(log₂n) 渐进运行时间的 BST 树的高度应接近于比 log₂n 小的最大整数。

但实际问题是：

如何保证 BST 的拓扑结构始终保持树高度与节点数量的最佳比例？

因为 BST 的拓扑结构与节点的插入顺序息息相关，一种方式是通过数据的乱序来保证。所以必须在插入节点前就得到数据。

但是如果无法掌控数据的来源，怎么做？一种方案是新的节点插入不会打乱BST树的平衡。这种始终维持树的平衡状态的数据结构称为：自平衡二叉查找树。self-balancing binary search tree.

一棵平衡树

指的是树能够保持其高度与广度能够保持预先定义的比例。有许多种不同的自平衡 BST 数据结构，例如 AVL 树、红黑树（Red-Black Tree）、2-3 树、2-3-4 树、伸展树（Splay Tree）、B 树等等。

---

AVL树

1962年, 数学家发明的第一种自平衡二叉查找树，以其名字命名。它的平衡条件是，对每个节点n:

节点n的左子树的高度与右子树的高度差最多是1。即可以没有高度差，也可以高度差距1.

树的高度可递归性定义为：

• 如果节点n没有子节点，则它的高度为 0；
• 如果节点n只有一个子节点，则n的高度为该子节点的高度加 1；
• 如果节点n有两个子节点，则n的高度为两个子节点中高度较高的加 1；
• 如果节点没有子节点，无子节点侧的高度是-1。

例子：

下面有4个BST树，节点中的数代表节点的值，左右两侧的数代表左右子树的高度。a, b是AVL树，c,d不是，因为c/d不满足AVL的平衡条件。

当创建一棵 AVL 树时，难点在于如何保证 AVL 的平衡性质要求，而不用关注对树的具体操作。也就是说，无论是向树添加节点还是删除节点，最重要的事情就是保持树的平衡。

AVL 树通过 "旋转操作（rotations）" 来保持树的平衡。旋转操作可以重塑树的拓扑结构来恢复树的平衡，更重要的是，重塑后的树依然符合二叉查找树的性质要求。

当向一棵 AVL 树中插入一个新的节点时，需要经过两阶段的过程。

1. 插入新节点的操作将使用与向 BST 树中插入新节点时使用的相同的查找算法。新的节点将做为一个叶子节点被添加到树中合适的位置，以满足 BST 的性质要求。在添加完节点后，将导致树的结构可能已经违背 AVL 树的性质要求。
2. 在第二个阶段中，将遍历访问路径，来检查每个节点左右子树高度。如果存在某节点的左右子树的高度差大于 1 时，则需要使用旋转操作来处理。

例子：

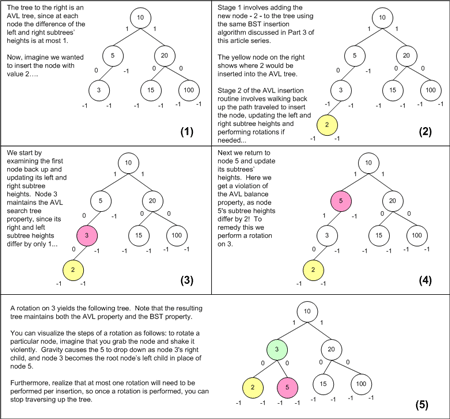
有时除了像上图中描述的简单的旋转操作之外，可能还需要进行多次旋转操作。最重要的就是要意识到插入操作和删除操作都会破坏 AVL 树的平衡，而旋转操作就是解决这些问题的法宝。

通过确保所有节点的左右子树的差小于等于 1，AVL 树保证了插入、删除和查找操作将始终保持 O(log₂n) 的渐进运行时间，而与插入或删除节点的顺序无关。

---

2-3树

参考：浅谈算法和数据结构: 八 平衡查找树之2-3树

2-3树是多叉树，它同样是一个平衡查找树。

二叉树中，每个节点最多只储存一个数据项的同时，最多也只有左右两条链接。而2-3树则不同：

定义

2-3树是一个多叉树。一个节点可以保存1个或2个数据项。可以有0-3个子节点。

1. 有一个数据项的节点必须有2个子节点。
2. 有二个数据项的节点必须有3个子节点。
3. 每个节点的数据项按照，数据项的key，从左到右保持从小到大的顺序。
4. 两个key之间的子树的key的值，大于父节点左key，小于父节点的右key.
5. 作为平衡树，所有从leaf到root的path的高度相同，因此所有的叶子节点都是位于同一层。
6. ⚠️2-3树的节点分裂是：自底向上的（不能预分裂），而且2-3树节点分裂必须用到新数据项。
7. 由1，2可知，除了叶节点不允许出现空节点。

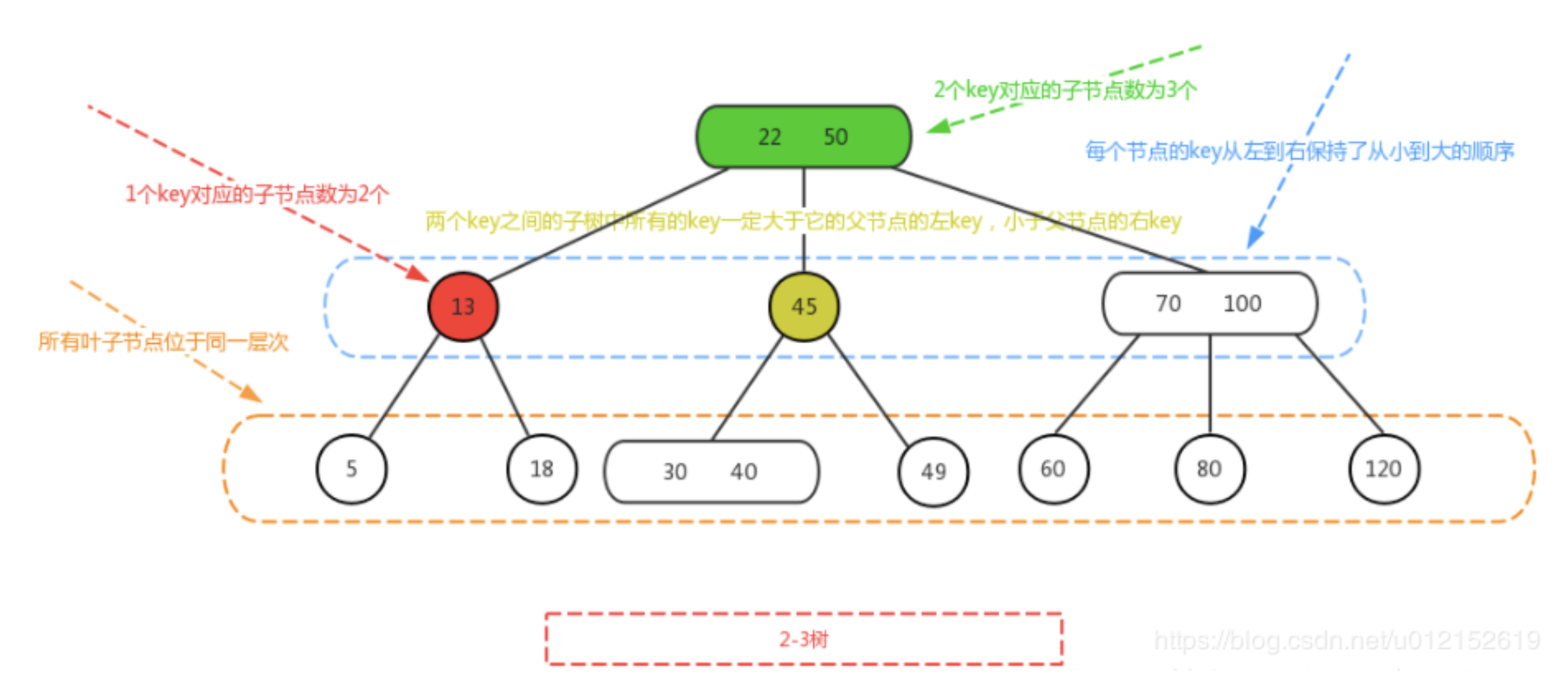
时间复杂度：

• 在最坏的情况下，也就是所有的节点都是2-node节点，查找效率为lgN
• 在最好的情况下，所有的节点都是3-node节点，查找效率为log₃N约等于0.631lgN

原理：

2-3树在插入key值的过程中会不断构建并分解3-key节点来保持树的平衡，因此在2-3树就可以避免二叉树的不平衡导致的效率低下的问题。

2-3树是自平衡的树，例如插入一组从小到大的key值的元素：

1. 首先2-3树已经构建一个根节点
2. 然后插入值为1的key。（⚠️2-3树允许一个节点储存两个key值）
3. 插入2。成为了临时的3key节点，这是2-3树不允许的，需要分裂，并把1上传，形成二叉树结构。
4. 插入3。⚠️这时的2-3树是左右平衡的。
5. 再插入4。形成了3-key节点，需要分解它，并导致树的不平衡。（⚠️定义所有叶节点都在同一层）
6. 重构，把节点3和节点1合并。成为一个2-3树。
7. 再插入5。然后插入6，形成一个3key节点。分解它，上传5节点。根节点形成3-key节点，树虽然平衡，但不符合2-3树的定义：每个节点最多有2个数据key。
8. 分解root节点：最后的树是左右平衡的。

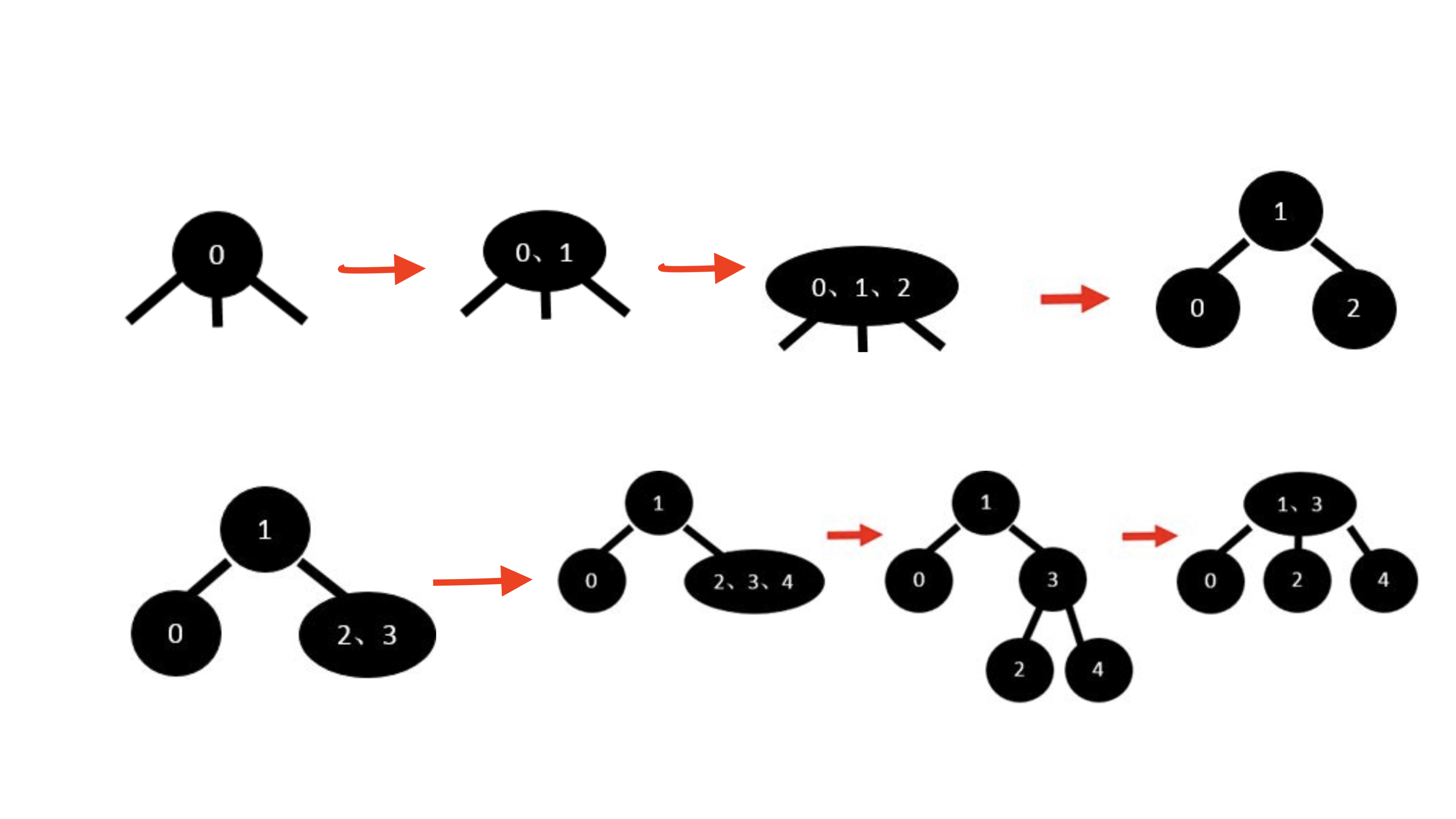
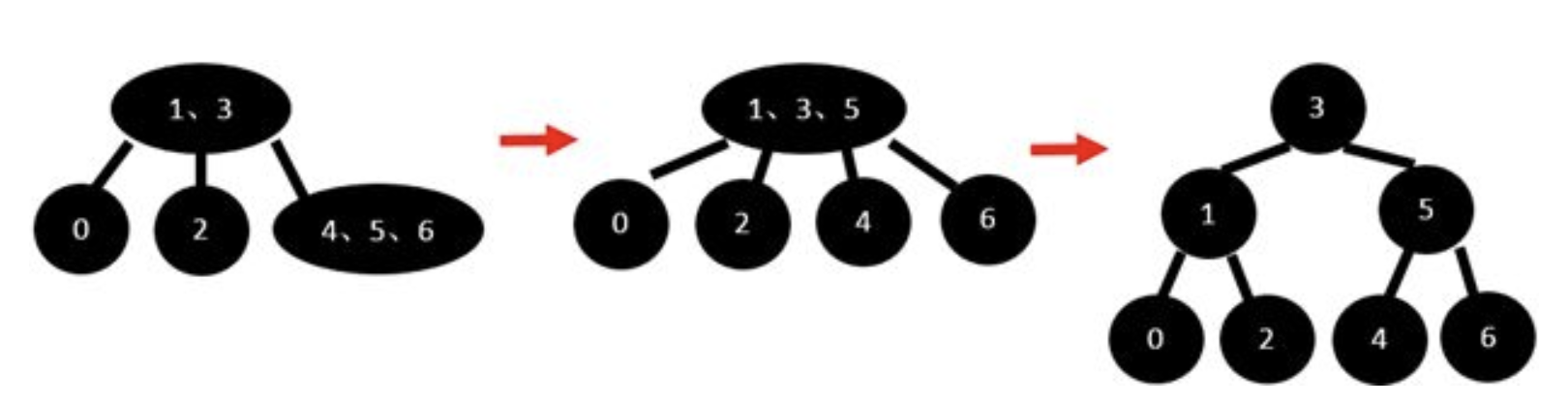
由此可知，2-3树可以避免二叉搜索树的不平衡导致的效率低下的问题。

总结-插入方法：

1. 如果2-3树已存在当前插入的key，则插入失败，正确的插入一定是在叶子节点内插入。
2. 如果等待插入的节点内只有一个节点，则直接插入。
3. 如果等待插入的节点内有2个节点，插入后，需要对节点分裂。形成一个二叉树结构，然后将父节点再向上传递。
4. 重复2和3的步骤，直到满足2-3树的定义。

删除方法：

比较复杂，未细看。参考：https://blog.csdn.net/u012152619/article/details/84332165

首先找到所在要删除的关键字(假设是K)所在的节点。

如果这个节点不是叶节点，就要找到中序排列时K后面的关键字所在的节点，这个节点一定是叶节点（因为它在右子树中是最小的）。然后交换这两个节点，那么所删除的关键字最终还是在一个叶节点中。

如果这个节点是叶节点，分叶节点和非叶节点，再根据key的数量分为4种：

• 1key的叶节点
• 2key的叶节点
• 1key的非叶节点
• 2key的非叶节点

下面从简单到复杂情况分析：

1. 如果删除的节点是2key的叶节点，只需删除目标key即可。2key叶节点变为1key叶节点，仍是2-3树。

    10               10
  /     \      =>  /   \
 4,6     18       4，x  18

2. 如果删除的节点属于2key非叶节点，则中序遍历找到待删除节点的后继节点，然后将后继节点和待删除节点位置交换。 此时问题转化为删除节点为叶子节点了。这时有2种情况：

• 待删除节点位于一个2-key叶节点内。删除方法见方法1。

       10， 20                             12，20
    /     |      \        =>           /     |     \
 4     12, 15    25                   4    x ,15    25
#直接删除10即可。

• 待删除节点是一个独立的叶子节点。  删除方法见