HDU - 3586 Information Disturbing 树形dp二分答案

HDU - 3586 Information Disturbing

　　题目大意：从敌人司令部（1号节点）到前线（叶子节点）的通信路径是一个树形结构，切断每条边的联系都需要花费w权值，现在需要你切断前线和司令部的连接，（就是所有叶子节点都到不了根节点），并且总花费不能超过m。问能够实行的方案中，最大花费的最小值，否则输出-1.

　　树形dp的题还是很好意识到用树形dp的，但最好是画一画图进行理解和推导，就像现在我随手画的图（第一次发现可以传图片）。

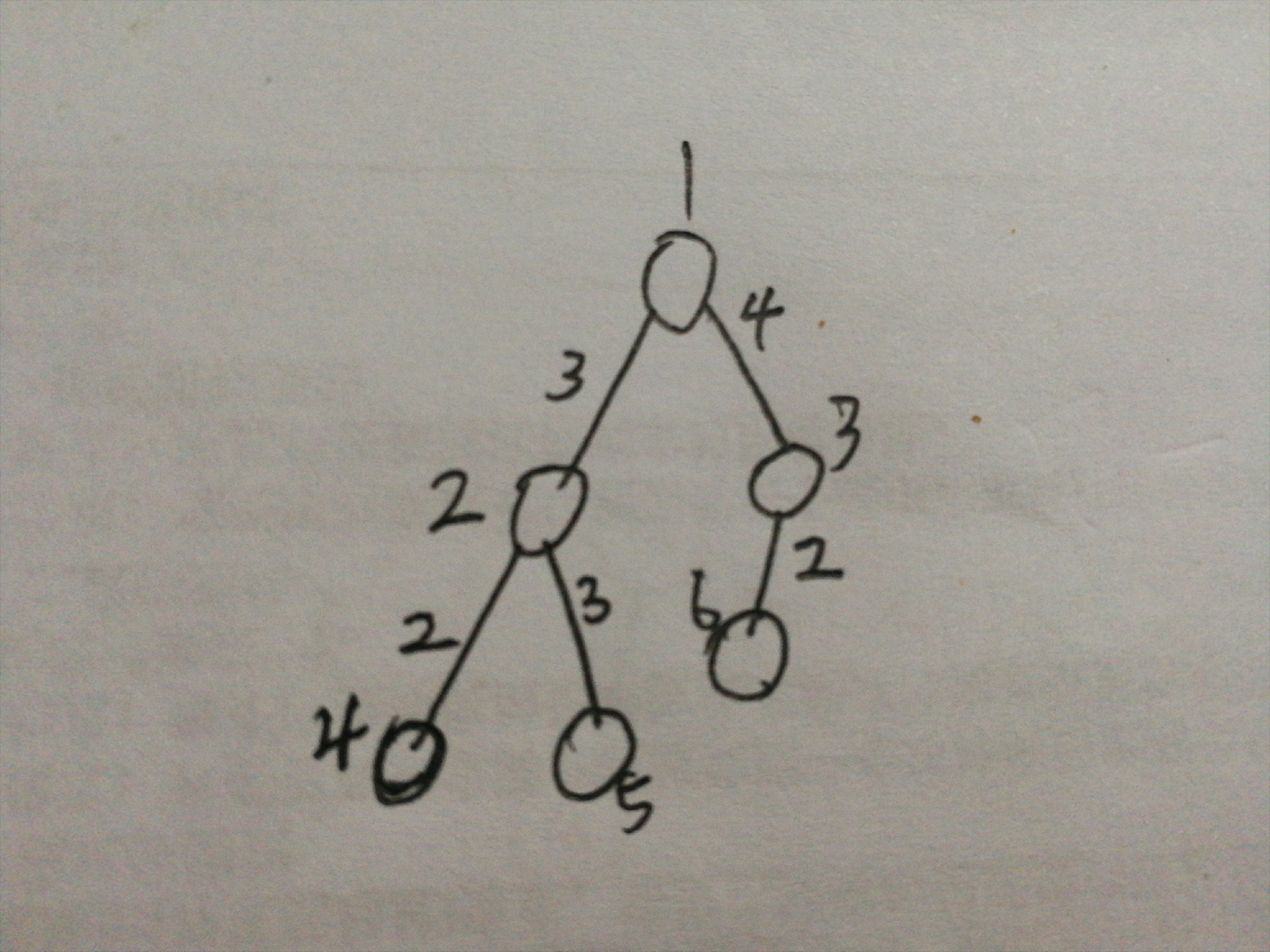（画得有点小丑，问题不大）

　　现在回到问题，就是我们需要切断1和4,5,6节点联系，那我们有几种选择呢，首先现在6节点,6节点只和3节点相连，3节点和1节点相连，那我们可以通过切断1和3的联系，或者是切断3和6的联系，来实现切断1和6的连接，很明显我们会选择3和6的联系，因为它们的权值较小。推理到左边，要切断1和4,5的联系就有，一.切断1和2的联系，二。切断2和3以及切断2和5的联系这两种，很明显我们会选择切断1和3的联系。我们可以发现如果我们把每个节点视为根节点的话，要切断它和叶子节点的关系无非有两种联系，切断它和它下一级的节点的联系，或者它下一级的节点切断和它所有节点的联系。我们用dp[i]来表示i节点切断它和它所有叶子节点的总花费最小值就有

（字也丑。。。）

　　但现在问题是要找到的是一个最大花费的最小值，如果我们直接树形dp跑一遍的话就只能找到一个方案，并且其中的最大值不一定就是最小的，所以我们需要二分一个答案，然后用这个答案作为一个限制去跑树形dp看该方案可不可行？那么怎么实现这个限制呢？我想到的是如果一条边的权值已经大于限制值了，那就让它等于m+1，这样的话如果没有其他能代替它的更小的边，最终总花费肯定是大于m的，也就是方案不可行。其他细节详情见代码如下

　　

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 const int N=;
 struct Side{
     int v,ne,w;
 }S[*N];
 int sn,n,m,head[N],dp[N];
 void add(int u,int v,int c)
 {
     S[sn].v=v;
     S[sn].w=c;
     S[sn].ne=head[u];
     head[u]=sn++;
 }
 int dfs(int u,int f,int lim)
 {
     dp[u]=;
     for(int i=head[u];i!=-;i=S[i].ne)
     {
         int v=S[i].v;
         if(v!=f)
         {
             dfs(v,u,lim);
             int cost=(S[i].w>lim ? m+ : S[i].w);//如果权值超过限制，设为m+1
             dp[u]+=min(dp[v],cost);//子节点的花费以及相连的边权值中取个最小值
             //当前节点加上所有子节点需要切断和叶子节点的花费
         }
     }
     if(dp[u]==)//这个是用来判断它是不是叶子节点的
         dp[u]=0x3f3f3f3f;//叶子节点的dp设个最大值，它的父节点只能切断和它相连的边
     return dp[u];
 }
 int main()
 {
     int a,b,w;
     while(scanf("%d%d",&n,&m)&&(n||m))
     {
         for(int i=;i<=n;i++)
             head[i]=-;
         int l=,r=;//l所有边中的最小值，r所有边中的最大值
         sn=;
         for(int i=;i<n;i++)
         {
             scanf("%d%d%d",&a,&b,&w);
             add(a,b,w);
             add(b,a,w);
             l=min(l,w);
             r=max(r,w);
         }
         int ans=-;
         while(l<=r)
         {
             int mid=(l+r)>>;
             if(dfs(,,mid)<=m)//判断这个答案是否可行
                 ans=mid,r=mid-;//可行的话，继续调小
             else
                 l=mid+;
         }
         printf("%d\n",ans);
     }
     return ;
 }

太君这边请~