python 牛顿迭代法

使用牛顿迭代法求方程 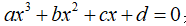 在x附近的一个实根。

赋值X,即迭代初值；用初值x代入方程中计算此时的f(x)=(a * x * x * x + b * x * x + c * x + d)和f’(x)=(3 * a * x * x + 2 * b * x + c)

计算增量f(x)/f’(x)；计算下一个x: x-f(x)/f’(x);   把新产生的x替换 x: x=x-f(x)/f’(x)，循环;  

若d绝对值大于0.00001，则重复上述步骤。

def diedai(a, b, c, d,X):
    x = X
    if a == 0 and c ** 2 - 4 * b * d < 0:
        print("无解")
    elif a == 0 and b == 0 and c == 0 and d != 0:
        print("无解")
    elif a == 0 and b == 0 and c == 0 and d == 0:
        print("恒等")
    else:
        while abs(a * x * x * x + b * x * x + c * x + d) > 0.000001:
            x = x - (a * x * x * x + b * x * x + c * x + d) / (3 * a * x * x + 2 * b * x + c)
        print("x=%.2f" % x)

a,b,c,d,x=input().split()
diedai(int(a),int(b),int(c),int(d),int(x))