scikit-learn机器学习(三)多项式回归(二阶，三阶，九阶)

我们仍然使用披萨直径的价格的数据

import matplotlib

matplotlib.rcParams['font.sans-serif']=[u'simHei']

matplotlib.rcParams['axes.unicode_minus']=False

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

from sklearn.preprocessing import PolynomialFeatures

X_train = [[6],[8],[10],[14],[18]]

y_train = [[7],[9],[13],[17.5],[18]]

X_test = [[6],[8],[11],[16]]

y_test = [[8],[12],[15],[18]]

LR = LinearRegression()

LR.fit(X_train,y_train)

xx = np.linspace(0,26,100)

yy = LR.predict(xx.reshape(xx.shape[0],1))

plt.plot(xx,yy)

二阶多项式回归

# In[1] 二次回归，二阶多项式回归

#PolynomialFeatures转换器可以用于为一个特征表示增加多项式特征

quadratic_featurizer = PolynomialFeatures(degree=2)

X_train_quadratic = quadratic_featurizer.fit_transform(X_train)

X_test_quadratic = quadratic_featurizer.transform(X_test)

regressor_quadratic = LinearRegression()

regressor_quadratic.fit(X_train_quadratic,y_train)

xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0],1))

yy_quadratic = regressor_quadratic.predict(xx_quadratic)

plt.plot(xx,yy_quadratic,c='r',linestyle='--')

# In[2] 图参数，输出结果

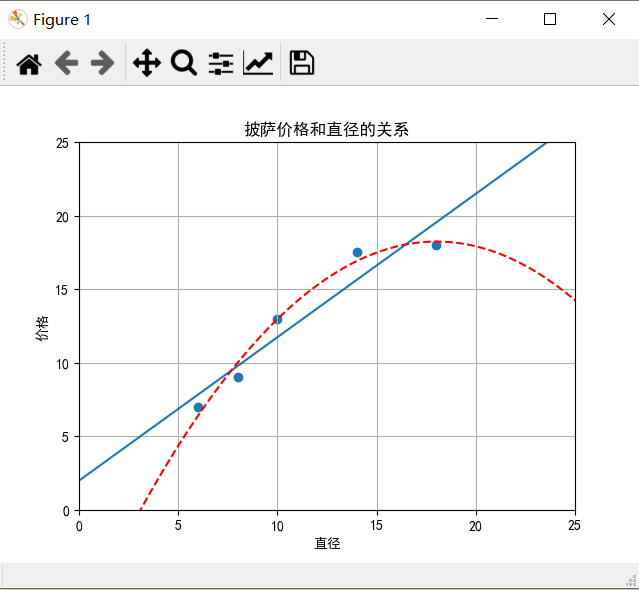
plt.title("披萨价格和直径的关系")

plt.xlabel("直径")

plt.ylabel("价格")

plt.axis([0,25,0,25])

plt.grid(True)

plt.scatter(X_train,y_train)

print("X_train\n",X_train)

print("X_train_quadratic\n",X_train_quadratic)

print("X_test\n",X_test)

print("X_test_quadratic\n",X_test_quadratic)

print("简单线性规划R方",LR.score(X_test,y_test))

print("二阶多项式回归R方",regressor_quadratic.score(X_test_quadratic,y_test))

X_train

 [[6], [8], [10], [14], [18]]

X_train_quadratic

 [[  1.   6.  36.]

 [  1.   8.  64.]

 [  1.  10. 100.]

 [  1.  14. 196.]

 [  1.  18. 324.]]

X_test

 [[6], [8], [11], [16]]

X_test_quadratic

 [[  1.   6.  36.]

 [  1.   8.  64.]

 [  1.  11. 121.]

 [  1.  16. 256.]]

简单线性规划R方 0.809726797707665

三阶多项式回归

# In[3] 尝试三阶多项式回归

cubic_featurizer = PolynomialFeatures(degree=3)

X_train_cubic = cubic_featurizer.fit_transform(X_train)

X_test_cubic = cubic_featurizer.transform(X_test)

regressor_cubic = LinearRegression()

regressor_cubic.fit(X_train_cubic,y_train)

xx_cubic = cubic_featurizer.transform(xx.reshape(xx.shape[0],1))

yy_cubic = regressor_cubic.predict(xx_cubic)

plt.plot(xx,yy_cubic,c='g',linestyle='--')

plt.show()

print("X_train\n",X_train)

print("X_train_cubic\n",X_train_cubic)

print("X_test\n",X_test)

print("X_test_cubic\n",X_test_cubic)

print("三阶多项式回归R方",regressor_cubic.score(X_test_cubic,y_test))

X_train

 [[6], [8], [10], [14], [18]]

X_train_cubic

 [[1.000e+00 6.000e+00 3.600e+01 2.160e+02]

 [1.000e+00 8.000e+00 6.400e+01 5.120e+02]

 [1.000e+00 1.000e+01 1.000e+02 1.000e+03]

 [1.000e+00 1.400e+01 1.960e+02 2.744e+03]

 [1.000e+00 1.800e+01 3.240e+02 5.832e+03]]

X_test

 [[6], [8], [11], [16]]

X_test_cubic

 [[1.000e+00 6.000e+00 3.600e+01 2.160e+02]

 [1.000e+00 8.000e+00 6.400e+01 5.120e+02]

 [1.000e+00 1.100e+01 1.210e+02 1.331e+03]

 [1.000e+00 1.600e+01 2.560e+02 4.096e+03]]

三阶多项式回归R方 0.8356924156036954

九阶多项式回归

# In[4] 尝试九阶多项式回归

nine_featurizer = PolynomialFeatures(degree=9)

X_train_nine = nine_featurizer.fit_transform(X_train)

X_test_nine = nine_featurizer.transform(X_test)

regressor_nine = LinearRegression()

regressor_nine.fit(X_train_nine,y_train)

xx_nine = nine_featurizer.transform(xx.reshape(xx.shape[0],1))

yy_nine = regressor_nine.predict(xx_nine)

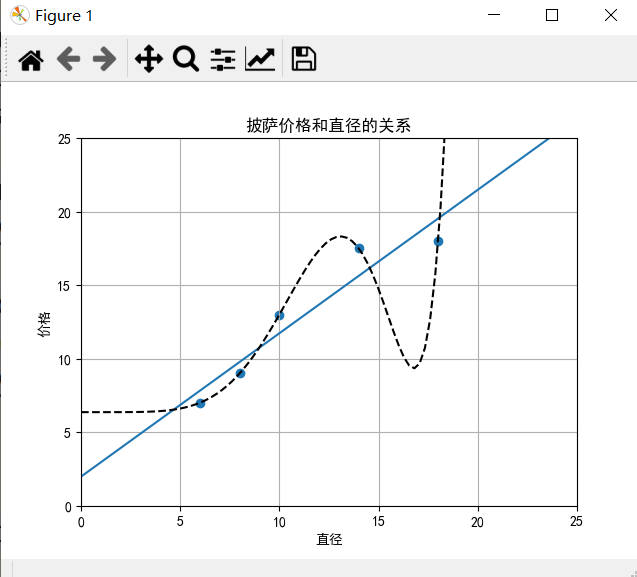
plt.plot(xx,yy_nine,c='k',linestyle='--')

plt.show()

print("X_train\n",X_train)

print("X_train_nine\n",X_train_nine)

print("X_test\n",X_test)

print("X_test_nine\n",X_test_nine)

print("九阶多项式回归R方",regressor_nine.score(X_test_nine,y_test))

X_train

 [[6], [8], [10], [14], [18]]

X_train_nine

 [[1.00000000e+00 6.00000000e+00 3.60000000e+01 2.16000000e+02

  1.29600000e+03 7.77600000e+03 4.66560000e+04 2.79936000e+05

  1.67961600e+06 1.00776960e+07]

 [1.00000000e+00 8.00000000e+00 6.40000000e+01 5.12000000e+02

  4.09600000e+03 3.27680000e+04 2.62144000e+05 2.09715200e+06

  1.67772160e+07 1.34217728e+08]

 [1.00000000e+00 1.00000000e+01 1.00000000e+02 1.00000000e+03

  1.00000000e+04 1.00000000e+05 1.00000000e+06 1.00000000e+07

  1.00000000e+08 1.00000000e+09]

 [1.00000000e+00 1.40000000e+01 1.96000000e+02 2.74400000e+03

  3.84160000e+04 5.37824000e+05 7.52953600e+06 1.05413504e+08

  1.47578906e+09 2.06610468e+10]

 [1.00000000e+00 1.80000000e+01 3.24000000e+02 5.83200000e+03

  1.04976000e+05 1.88956800e+06 3.40122240e+07 6.12220032e+08

  1.10199606e+10 1.98359290e+11]]

X_test

 [[6], [8], [11], [16]]

X_test_nine

 [[1.00000000e+00 6.00000000e+00 3.60000000e+01 2.16000000e+02

  1.29600000e+03 7.77600000e+03 4.66560000e+04 2.79936000e+05

  1.67961600e+06 1.00776960e+07]

 [1.00000000e+00 8.00000000e+00 6.40000000e+01 5.12000000e+02

  4.09600000e+03 3.27680000e+04 2.62144000e+05 2.09715200e+06

  1.67772160e+07 1.34217728e+08]

 [1.00000000e+00 1.10000000e+01 1.21000000e+02 1.33100000e+03

  1.46410000e+04 1.61051000e+05 1.77156100e+06 1.94871710e+07

  2.14358881e+08 2.35794769e+09]

 [1.00000000e+00 1.60000000e+01 2.56000000e+02 4.09600000e+03

  6.55360000e+04 1.04857600e+06 1.67772160e+07 2.68435456e+08

  4.29496730e+09 6.87194767e+10]]

九阶多项式回归R方 -0.09435666704291412

所有代码

# -*- coding: utf-8 -*-

import matplotlib

matplotlib.rcParams['font.sans-serif']=[u'simHei']

matplotlib.rcParams['axes.unicode_minus']=False

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

from sklearn.preprocessing import PolynomialFeatures

X_train = [[6],[8],[10],[14],[18]]

y_train = [[7],[9],[13],[17.5],[18]]

X_test = [[6],[8],[11],[16]]

y_test = [[8],[12],[15],[18]]

LR = LinearRegression()

LR.fit(X_train,y_train)

xx = np.linspace(0,26,100)

yy = LR.predict(xx.reshape(xx.shape[0],1))

plt.plot(xx,yy)

# In[1] 二次回归，二阶多项式回归

#PolynomialFeatures转换器可以用于为一个特征表示增加多项式特征

quadratic_featurizer = PolynomialFeatures(degree=2)

X_train_quadratic = quadratic_featurizer.fit_transform(X_train)

X_test_quadratic = quadratic_featurizer.transform(X_test)

regressor_quadratic = LinearRegression()

regressor_quadratic.fit(X_train_quadratic,y_train)

xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0],1))

yy_quadratic = regressor_quadratic.predict(xx_quadratic)

plt.plot(xx,yy_quadratic,c='r',linestyle='--')

# In[2] 图参数，输出结果

plt.title("披萨价格和直径的关系")

plt.xlabel("直径")

plt.ylabel("价格")

plt.axis([0,25,0,25])

plt.grid(True)

plt.scatter(X_train,y_train)

print("X_train\n",X_train)

print("X_train_quadratic\n",X_train_quadratic)

print("X_test\n",X_test)

print("X_test_quadratic\n",X_test_quadratic)

print("简单线性规划R方",LR.score(X_test,y_test))

print("二阶多项式回归R方",regressor_quadratic.score(X_test_quadratic,y_test))

# In[3] 尝试三阶多项式回归

cubic_featurizer = PolynomialFeatures(degree=3)

X_train_cubic = cubic_featurizer.fit_transform(X_train)

X_test_cubic = cubic_featurizer.transform(X_test)

regressor_cubic = LinearRegression()

regressor_cubic.fit(X_train_cubic,y_train)

xx_cubic = cubic_featurizer.transform(xx.reshape(xx.shape[0],1))

yy_cubic = regressor_cubic.predict(xx_cubic)

plt.plot(xx,yy_cubic,c='g',linestyle='--')

plt.show()

print("X_train\n",X_train)

print("X_train_cubic\n",X_train_cubic)

print("X_test\n",X_test)

print("X_test_cubic\n",X_test_cubic)

print("三阶多项式回归R方",regressor_cubic.score(X_test_cubic,y_test))

# In[4] 尝试九阶多项式回归

nine_featurizer = PolynomialFeatures(degree=9)

X_train_nine = nine_featurizer.fit_transform(X_train)

X_test_nine = nine_featurizer.transform(X_test)

regressor_nine = LinearRegression()

regressor_nine.fit(X_train_nine,y_train)

xx_nine = nine_featurizer.transform(xx.reshape(xx.shape[0],1))

yy_nine = regressor_nine.predict(xx_nine)

plt.plot(xx,yy_nine,c='k',linestyle='--')

plt.show()

print("X_train\n",X_train)

print("X_train_nine\n",X_train_nine)

print("X_test\n",X_test)

print("X_test_nine\n",X_test_nine)

print("九阶多项式回归R方",regressor_nine.score(X_test_nine,y_test))

scikit-learn机器学习(三)多项式回归(二阶，三阶，九阶)的更多相关文章

(原创)（三）机器学习笔记之Scikit Learn的线性回归模型初探
一.Scikit Learn中使用estimator三部曲 1. 构造estimator 2. 训练模型:fit 3. 利用模型进行预测:predict 二.模型评价模型训练好后,度量模型拟合效果的 ...
Scikit Learn: 在python中机器学习
转自:http://my.oschina.net/u/175377/blog/84420#OSC_h2_23 Scikit Learn: 在python中机器学习 Warning 警告:有些没能理解的 ...
(原创)（四）机器学习笔记之Scikit Learn的Logistic回归初探
目录 5.3 使用LogisticRegressionCV进行正则化的 Logistic Regression 参数调优一.Scikit Learn中有关logistics回归函数的介绍 1. 交叉 ...
scikit learn 模块调参 pipeline+girdsearch 数据举例：文档分类（python代码）
scikit learn 模块调参 pipeline+girdsearch 数据举例:文档分类数据集 fetch_20newsgroups #-*- coding: UTF-8 -*- import ...
TensorFlow 便捷的实现机器学习三
TensorFlow 便捷的实现机器学习三 MNIST 卷积神经网络 Fly Overview Enabling Logging with TensorFlow Configuring a Vali ...
【机器学习】多项式回归sklearn实现
[机器学习]多项式回归原理介绍 [机器学习]多项式回归python实现 [机器学习]多项式回归sklearn实现使用sklearn框架实现多项式回归.使用框架更方便,可以少写很多代码. 使用一个简单 ...
【机器学习】多项式回归python实现
[机器学习]多项式回归原理介绍 [机器学习]多项式回归python实现 [机器学习]多项式回归sklearn实现使用python实现多项式回归,没有使用sklearn等机器学习框架,目的是帮助理解算 ...
Scikit Learn
Scikit Learn Scikit-Learn简称sklearn,基于 Python 语言的,简单高效的数据挖掘和数据分析工具,建立在 NumPy,SciPy 和 matplotlib 上.
机器学习框架Scikit Learn的学习
一安装安装pip 代码如下:# wget "https://pypi.python.org/packages/source/p/pip/pip-1.5.4.tar.gz#md5=83 ...

随机推荐

页面Header自适应屏幕
<!DOCTYPE html> <html lang="zh-CN"> <head> <meta charset="utf-8& ...
c++对象模型和RTTI(runtime type information)
在前面已经探讨过了虚继承对类的大小的影响,这次来加上虚函数和虚继承对类的大小的影响. 先来回顾一下之前例子的代码: #include <iostream> using namespace ...
MySQl 进阶一基本查询及练习
知识点及练习 USE myemployees; #.查询表中的单个字段 SELECT last_name FROM employees; #.查询表中多个字段 #.查询全部 SELECT * FROM ...
0008SpringBoot中的spring.config.location对于运维的用处
在工作过程中,若项目已经打好包,application.properties中的配置文件已经不能修改,但是还是需要修改一些参数或者新增一些参数的情况下怎么办? 可以单独再定义一个配置文件,比如定义名称 ...
实例化Vue时的两种挂载方式el与$mount
el 与mount 都是挂载. el vue官网的介绍https://cn.vuejs.org/v2/api/#el mount vue官网的介绍 https://cn.vuejs.org/v2/ap ...
linux mint安装mysql-8.0.16
1.使用通用二进制文件在Unix / Linux上安装MySQL 下载的文件:mysql-8.0.16-linux-glibc2.12-x86_64.tar.xz 注意: 如果您以前使用操作系统本机程 ...
Python 10--模块
可以在模块中,直接使用__file__,识别出该模块文件的路径. print __file__
list，tuple,set,dict基础
list # @Auther : chen # @Time : 2018/4/26 19:55 # @File : list_ex.py # @SoftWare : PyCharm # list1 = ...
yii 查询垃圾分类接口
public function actionGarbage() { // $param = \Yii::$app->request->post('rubbish', ''); // 接收j ...
python以下划线开头的变量和函数的作用
在python中,我们经常能看到很多变量名以_下划线开头,而且下划线的数量还不一样,那么这些变量的作用到底是什么? 变量名分类: # 以数字.字母开头: 正常的公有变量名a = 1def aa(): ...

scikit-learn机器学习(三)多项式回归(二阶，三阶，九阶)

scikit-learn机器学习(三)多项式回归(二阶，三阶，九阶)的更多相关文章

随机推荐

热门专题