冲刺Noip2017模拟赛5 解题报告——五十岚芒果酱

1. 公约数（gcd）

【问题描述】
给定一个正整数，在[,n]的范围内，求出有多少个无序数对(a,b)满足
gcd(a,b)=a xor b。
【输入格式】
输入共一行，一个正整数n。
【输出格式】
输出共一行，一个正整数表示答案。
【输入输出样例】
gcd .in gcd .out
 
解释：只有(,)满足要求
【数据范围】
对于30%的数据满足n<=
对于60%的数据满足n<=^
对于100%的数据满足n<=^

题目

tag：数学

思路：就一个等式，gcd(a,b)==d==a^b，我们要把它扩展开来，由于a==b无解，设a严格大于b，d|a，d|b==〉d|(a-b)，则a-b>=d=gcd(a,b)。a^b显然>=a-b，因为每一位异或的结果要么比减法大要么跟减法一样。最后得gcd(a,b)<=a-b<=a^b。现在看需要枚举啥子，取特 gcd(a,b)=a-b=a^b=d，运用异或的性质得a^d=b代回去，a-a^d=d,移项a-d=a^d，枚举d和d的倍数即可。这个算法的时间复杂度是O（nlogn）。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 using namespace std;
 int n,ans;
 int main()
 {
     //freopen("gcd.in","r",stdin);
     //freopen("gcd.out","w",stdout);
     scanf("%d",&n);
     for(int i=;i<=n;++i)
         for(int j=n/i;j>=;--j){
             int a=i*j;
             if((a-i)==(a^i)) ans++;
         }
     printf("%d",ans);
     return ;
 }

2. 通讯（message）

【问题描述】“这一切都是命运石之门的
选择。”
试图研制时间机器的机关 SERN 截获了中二科学家伦太郎发往过去的一条
短信，并由此得知了伦太郎制作出了电话微波炉（仮）。
为了掌握时间机器的技术，SERN 总部必须尽快将这个消息通过地下秘密通讯
网络，传达到所有分部。
SERN 共有 N 个部门（总部编号为 ），通讯网络有 M 条单向通讯线路，每条
线路有一个固定的通讯花费 Ci。
为了保密，消息的传递只能按照固定的方式进行：从一个已知消息的部门向
另一个与它有线路的部门传递（ 可能存在多条通信线路）。我们定义总费用为所
有部门传递消息的费用和。
幸运的是，如果两个部门可以 直接或间接地相互传递消息（即能按照上述方法
将信息由 X 传递到 Y，同时能由 Y 传递到 X），我们就可以忽略它们之间的花费。
由于资金问题（预算都花在粒子对撞机上了），SERN 总部的工程师希望知道，
达到目标的最小花费是多少。
【输入格式】多组数据，文件以
个  结尾。
每组数据第一行，一个整数 N，表示有 N 个包括总部的部门（从  开始编号）。
然后是一个整数 M，表示有 M 条单向通讯线路。
接下来 M 行，每行三个整数,Xi,Yi,Ci，表示第 i 条线路从 Xi 连向 Yi，花费
为
Ci。
【输出格式】
每组数据一行，一个整数表示达到目标的最小花费。
【输入输出样例】
message.in 
 
message.out
 
【样例解释】第一组数据：总部把消息传给分部 ，分部  再传给分
部 .总费用：
+=.
第二组数据：总部把消息传给分部 ，由于分部  和分部  可以互相传递消
息，所以分部  可以无费用把消息传给 .总费用：+=.
第三组数据：总部把消息传给分部 ，最小费用为 .总费用：.
【数据范围】对于 %的数据，
保证 M=N-
对于另 %的数据，N ≤  ，M ≤  对于 %的数据，N ≤  ，
M ≤ ^ ，Ci ≤ ^ ，数据组数 ≤
数据保证一定可以将信息传递到所有部门。

题目

tag：强连通分量，缩点，贪心

思路：tarjan求强连通分量，缩点后形成DAG的树状结构。乍一看是最小生成树，根据题意，除起点的每个点都有可以到它的边，既然最后都能到达，选最小的那个边就行了。如果用最小生成树，起点可能会“被”连接，用贪心法一开始把minv[st]置0可以避免这种情况。

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<stack>
 #define maxn 100010
 using namespace std;
 int cnt,tot,ans,n,m,num,dfn[maxn],low[maxn],vis1[maxn],vis2[maxn],hl[maxn],HL[maxn],jh[maxn],own[maxn],fa[maxn],minv[maxn];
 stack<int>S;
 struct Edge{
     int u,v,w,ne;
 }e[maxn<<],E[maxn<<];
 void init()
 {
     cnt=tot=ans=num=;
     memset(dfn,,sizeof(dfn));
     memset(low,,sizeof(low));
     memset(vis1,,sizeof(vis1));
     memset(vis2,,sizeof(vis2));
     memset(hl,,sizeof(hl));
     memset(HL,,sizeof(HL));
     memset(e,,sizeof(e));
     memset(E,,sizeof(E));
     memset(jh,,sizeof(jh));
     memset(own,,sizeof(own));
     memset(fa,,sizeof(fa));
     memset(minv,/,sizeof(minv));
 }
 void add(int u,int v,int w)
 {
     e[++cnt].u=u;
     e[cnt].v=v;
     e[cnt].w=w;
     e[cnt].ne=hl[u];
     hl[u]=cnt;
 }
 int find(int x)
 {
     return x==fa[x]?x:fa[x]=find(fa[x]);
 }
 void tarjan(int x)
 {
     S.push(x);
     dfn[x]=low[x]=++tot;
     vis1[x]=vis2[x]=;
     for(int i=hl[x];i;i=e[i].ne){
         int v=e[i].v;
         if(!vis1[v]){
             tarjan(v);
             low[x]=min(low[x],low[v]);
         }
         else if(vis2[v]) low[x]=min(low[x],dfn[v]);
     }
     if(dfn[x]==low[x]){
         num++;
         int now=-;
         while(now!=x){
             now=S.top();
             S.pop();
             jh[now]=num;
             own[num]++;
             vis2[now]=;
         }
     }
 }
 void rebuild()
 {
     for(int i=;i<n;++i)
         for(int j=hl[i];j;j=e[j].ne){
             int v=e[j].v;
             if(jh[i]!=jh[v]){
                 E[++cnt].u=jh[i];
                 E[cnt].v=jh[v];
                 E[cnt].w=e[j].w;
                 E[cnt].ne=HL[jh[i]];
                 HL[jh[i]]=cnt;
             }
         }
 }
 bool cmp(Edge x,Edge y)
 {
     return x.w<y.w;
 }
 int main()
 {
     //freopen("message.in","r",stdin);
     //freopen("message.out","w",stdout);
     int x,y,w;
     while(scanf("%d%d",&n,&m)!=EOF){
         init();
         if(!n&&!m) break;
         for(int i=;i<=m;++i){
             scanf("%d%d%d",&x,&y,&w);
             add(x,y,w);
         }
         for(int i=;i<n;++i) if(!vis1[i]) tarjan(i);
         cnt=tot=;
         rebuild();
         minv[jh[]]=;
         for(int i=;i<=num;++i)
             for(int j=HL[i];j;j=E[j].ne){
                 int v=E[j].v;
                 minv[v]=min(E[j].w,minv[v]);
             }
         for(int i=;i<=num;++i) ans+=minv[i];
         printf("%d\n",ans);
     }
     return ;
 }

3.label(label)

【问题描述】
Samjia和Peter不同，他喜欢玩树。所以Peter送给他一颗大小为n的树，节
点编号从1到n。
Samjia要给树上的每一个节点赋一个[,m]之间的权值，并使得有边直接相
连的两个节点的权值之差的绝对值 ≥ k。请你告诉Samjia有多少种不同的赋值
方案，只用求出答案对10
 +()取模得到的结果。
【输入格式】
输入文件名为 label.in。
输入数据的第一行包含一个整数 T，代表测试数据组数。
接下来是 T 组数据.
每组数据的第一行包含三个整数 n、m 和 k。
接下来 n −  行，每行包含两个整数 u 和 v， 代表节点 u 和 v 之间有
一条树边。
【输出格式】
输出文件名为 label.out。
对于每组数据，输出一行，包含一个整数，代表所求的答案。
【输入输出样例】
label.in label.out
 
【输入输出样例说明】
对于第一组样例，满足的方案如图
图中方括号内的数字（[x]）代表给节点赋的值。
【数据规模与约定】
测试点编号 m ≤ 特殊约定
,  无
,  无
, ^ 第2-n号节点与1号节点直接相连
, ^ 第i号节点与第i+1号节点直接相连
, ^ 无
对于所有数据，T≤,n≤,k≤,m≤^

题目

tag:树形DP

思路：对于这道树形DP来说，父节点的取值决定了子节点的取值范围，子节点的方案数通过使用加法原理和乘法原理继承给父节点。但暴力枚举只能拿到20分。我们运用数学归纳，发现对于每个节点X，满足f[x][i]=f[x][m-i+1]，也就是说它的取值是对称的。其实，如果可取的长度相等，DP（f）的值也相等。再考虑，如果当m特别大而k很小，就有很长一段区间内每个点的DP值都相等，如下图。

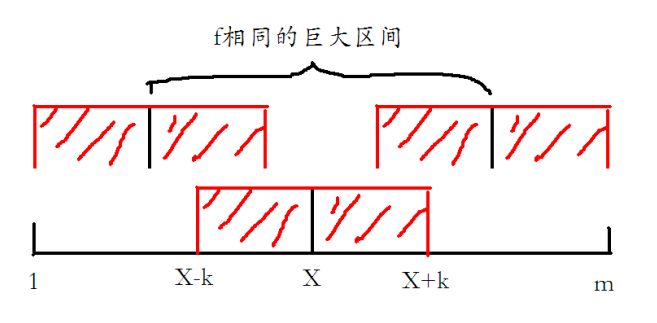
如果这两个区间同时向外移动，因为对称性，他们的值同步变化。那么，我们有必要把100 * 10^9 个值都存到数组里吗？答案当然是，没有。最多只会有(maxn-1)*maxk个不同的值，也就是说，我们只用保存最多9900（limit）个数，当调用时直接去找每个值存他的地方，把大区间分左（1~limit）、中(limit~m-limit)、右(m-limit~m)，在左区间直接调用，让limit储存中区间的所有点的那个相同值，在右区间，找左区间的对称点。

解决了空间问题，还有更麻烦的时间问题，我们每取一个值，都会生成完全不同的范围，如果每次都进行计算是不是太过麻烦？不过，很容易发现，从1取到limit，它们生成的区间有一定变化规律，大部分是不会变的，左右两端进行微调，右端退出，左端进入（详见注释）。

我们还需要求出当取值为1时的初始区间，之后才能在上面进行修改。getsum——左中右的处理方式各异，左右每个点值都不同，需要暴力枚举，中区间只求有多少个点再乘值。

还有个小技巧，k=0的时候直接快速幂m^n输出。最后的答案就是根节点所有DP值的和，我们用现成的getsum可以直接求。

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 #include<stack>
 #define maxn 10010
 #define ll long long
 using namespace std;
 const int mod = 1e9 + ;
 int ans,k,hl[maxn],fa[maxn],cnt,n,m,T,lim,f[][maxn];
 struct Edge{
     int u,v,w,ne;
 }e[maxn<<];
 void init()
 {
     memset(hl,,sizeof(hl));
     memset(fa,,sizeof(fa));
     memset(f,,sizeof(f));
     memset(e,,sizeof(e));
     cnt=ans=;
 }
 void add(int u,int v)
 {
     e[++cnt].u=u;
     e[cnt].v=v;
     e[cnt].ne=hl[u];
     hl[u]=cnt;
 }
 ll getsum(int x,int st)
 {
     ll ret=;
     for(int i=st;i<=lim;++i) ret=(ret+f[x][i])%mod;//起点在左区间 计算从起点到lim
     for(int i=m;i>m-lim&&i>lim&&i>=st;--i) ret=(ret+f[x][m-i+])%mod;//类似上一行 计算右区间
     int l=max(st,lim+),r=m-lim;//计算中区间范围
     int len=r-l+;
     if(len>) ret=(ret+1ll*len*f[x][lim]%mod)%mod;
     return ret;
 }
 void dfs(int x)
 {
     for(int i=hl[x];i;i=e[i].ne){
         int v=e[i].v;
         if(v==fa[x]) continue;
         fa[v]=x;
         dfs(v);
     }
     for(int i=;i<=lim;++i) f[x][i]=;
     for(int i=hl[x];i;i=e[i].ne){
         int v=e[i].v;
         if(v==fa[x]) continue;
         ll sum=getsum(v,k+);//初始值
         for(int j=;j<=lim;++j){
             if(j-k>=) sum=(sum+f[v][j-k])%mod;//左端点增加区间
             f[x][j]=1ll*f[x][j]*sum%mod;//乘法原理
             int bj=j+k;//右端点
             if(bj<=m){//右端点还在大范围内
                 if(m-bj+<=lim) bj=m-bj+;//将右区间定位到左区间
                 else if(bj>=lim) bj=lim;//中区间定位到lim点
                 sum=((sum-f[v][bj])%mod+mod)%mod;//右端点退出区间
             }
         }
     }
 }
 int ksm(int a,int B)
 {
     int x=a,b=B,ret=;
     while(b){
         if(b&) ret= 1ll*ret*x %mod;
         x= 1ll*x*x%mod;
         b>>=;
     }
     return ret;
 }
 int main()
 {
     //freopen("label.in","r",stdin);
     //freopen("label.out","w",stdout);
     int x,y;
     scanf("%d",&T);
     while(T--){
         init();
         scanf("%d%d%d",&n,&m,&k);
         for(int i=;i<n;++i){
             scanf("%d%d",&x,&y);
             add(x,y);
             add(y,x);
         }
         if(!k){
             printf("%d\n",ksm(m,n));
             continue;
         }
         lim=min(,m);
         dfs();
         printf("%d\n",getsum(,));
     }
     return ;
 }

---

↑系统自带分割线

芒果君：这次大——————翻车！！！然后订正+解题报告又弄了好久QAQ 无fa可说OTZ