统计学习方法 | 第3章 k邻近法 | 补充

namedtuple

不必再通过索引值进行访问，你可以把它看做一个字典通过名字进行访问，只不过其中的值是不能改变的。

 sorted()适用于任何可迭代容器，list.sort()仅支持list（本身就是list的一个方法）

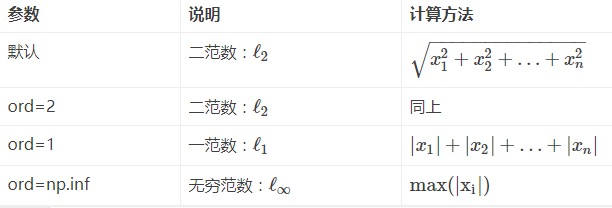
np.linalg.norm(求范数)

1、linalg=linear（线性）+algebra（代数），norm则表示范数。

2、函数参数

x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)

①x: 表示矩阵（也可以是一维）

②ord：范数类型

向量的范数：

train_test_split函数

用于将矩阵随机划分为训练子集和测试子集，并返回划分好的训练集测试集样本和训练集测试集标签。

格式：

X_train,X_test, y_train, y_test =cross_validation.train_test_split(train_data,train_target,test_size=0.3, random_state=0)

参数解释：

train_data：被划分的样本特征集

train_target：被划分的样本标签

test_size：如果是浮点数，在0-1之间，表示样本占比；如果是整数的话就是样本的数量

random_state：是随机数的种子。

随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。比如你每次都填1，其他参数一样的情况下你得到的随机数组是一样的。但填0或不填，每次都会不一样。

随机数的产生取决于种子，随机数和种子之间的关系遵从以下两个规则：

种子不同，产生不同的随机数；种子相同，即使实例不同也产生相同的随机数。

itertools

Python的内建模块itertools提供了非常有用的用于操作迭代对象的函数。

首先，我们看看itertools提供的几个“无限”迭代器：

>>> import itertools
>>> natuals = itertools.count(1)
>>> for n in natuals:
...     print n
...
1
2
3
...

因为count()会创建一个无限的迭代器，所以上述代码会打印出自然数序列，根本停不下来，只能按Ctrl+C退出。

cycle()会把传入的一个序列无限重复下去：

>>> import itertools
>>> cs = itertools.cycle('ABC') # 注意字符串也是序列的一种
>>> for c in cs:
...     print c
...
'A'
'B'
'C'
'A'
'B'
'C'
...

同样停不下来。

repeat()负责把一个元素无限重复下去，不过如果提供第二个参数就可以限定重复次数：

>>> ns = itertools.repeat('A', 10)
>>> for n in ns:
...     print n
...
打印10次'A'

无限序列只有在for迭代时才会无限地迭代下去，如果只是创建了一个迭代对象，它不会事先把无限个元素生成出来，事实上也不可能在内存中创建无限多个元素。

无限序列虽然可以无限迭代下去，但是通常我们会通过takewhile()等函数根据条件判断来截取出一个有限的序列：

>>> natuals = itertools.count(1)
>>> ns = itertools.takewhile(lambda x: x <= 10, natuals)
>>> for n in ns:
...     print n
...
打印出1到10