P5022 旅行

原题链接  https://www.luogu.org/problem/P5022

本着快csp了，做点往年的NOIp的题试试水来着，没想到水这么深 难度还挺大的，耗了我一天的时间（可能是我太菜了）

题目大意：

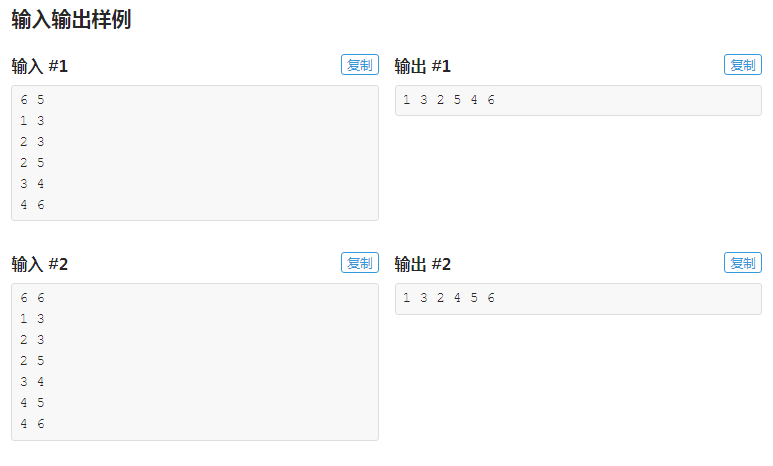
给你 n 个点和 m 条边，问如何遍历每个结点才能使最后的字典序最小，注意只有遍历完一棵字树的所有结点后才能回溯到他的父亲结点；

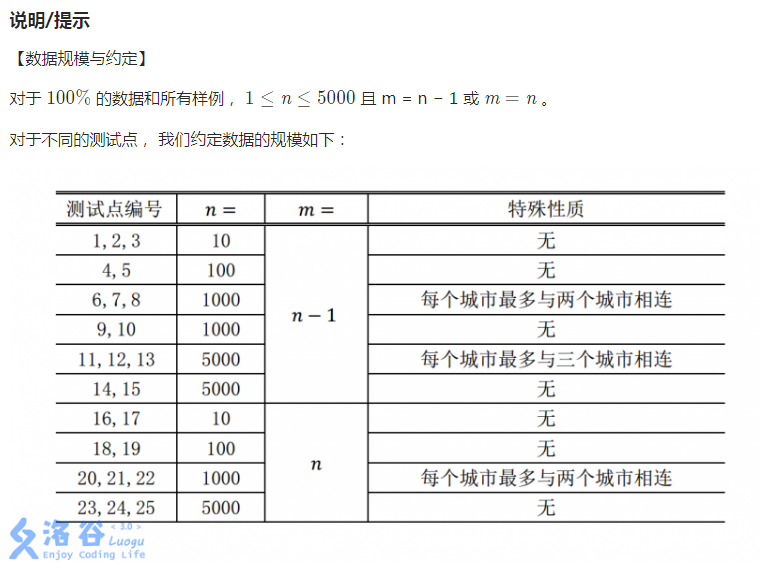
前 60 pts：

作为 NOIp2018 day2T1 来说，部分分确实给的挺足的，这 60 pts 就是哦；

看到 m = n-1 说明这是一棵树，考虑用搜索：

既然要保证是字典序最小，那么我们第一个点一定要选 1 了，考虑接下来只需要从他的儿子里按照编号从小到大遍历就好了，注意要遍历完一棵子树才能回溯上去；

后 40 pts：

m = n ？嗯，基环树！

所谓基环树，就是说在一个图里，有 n 个结点和 n 条边，那么这个图内有且仅有一个环；

我们仍然可以按照前 60 pts 的做法上去想：

按理来说我们遍历完 n 个结点只需要走 n-1 条边就好了啊，所以一定有一条边是多余的，也就是说我们根本遍历不到它，那么我们可以枚举每一条边，暂时把它删掉，然后和刚才的做法一样跑一遍 dfs，这样能求得一个字典序，我们取所有字典序中最小的一个就是答案了；

优化

显然如果我们像上述做法那样暴力的话，是会有几个点 TLE 的（毕竟NOIp也不会水到这种程度吧qwq），所以我们要考虑优化；

优化一：

题目中说了，我们的目的是遍历完每个点，那么假设我们删掉的边不是环上的边，那么这个图一定会变得不连通，那么就无法完成任务了；

所以我们只要找出基环树上的环，只需删掉环上的边就好了，至于找环嘛，这里我用的 tarjan（其实是只会这个qwq）

优化二：

最优性剪枝：假如我们在 dfs 的过程中，发现求得的字典序不如之前的答案优，那么我们直接可以 return 了；

有了这两个小优化，终于可以愉快的 AC 本题了，时间复杂度 O（n²）；

至于更神仙的 O（n log n）甚至 O（n）的做法，咕咕咕~

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
const int N=;
int n,m,bi,bj,tot,top,tim,start,edge_sum,scc_sum,ans_sum=;
int u[N],v[N],dfn[N],low[N],scc[N],st[N],vis[N],size[N],head[N],ans[N],f[N][N];
struct node
{
    int to,next;
}a[N<<];
void add(int from,int to)                 //链表存图
{
    edge_sum++;
    a[edge_sum].to=to;
    a[edge_sum].next=head[from];
    head[from]=edge_sum;
}
void tarjan(int u,int fa)                 //tarjan找环
{
    dfn[u]=low[u]=++tim;
    st[++top]=u;
    vis[u]=;
    for(int i=head[u];i;i=a[i].next)
    {
        int v=a[i].to;
        if(v==fa) continue;
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        scc_sum++;
        if(u==) start=scc_sum;
        while(st[top]!=u)
        {
            vis[st[top]]=;
            scc[st[top]]=scc_sum;
            top--;
        }
        vis[st[top]]=;
        scc[st[top]]=scc_sum;
        top--;
    }
}
void dfs(int u,int fa)
{
    tot++;
    if(u<ans[tot]||bj)        //如果比答案更优,或者之前就已经比答案优的话,就更新答案
    {
        bj=;                 //发现更优解了
        ans[tot]=u;
    }
    else if(u>ans[tot])       //最优性剪枝:不如答案优就直接返回
    {
        bi=;                 //没有找到更优解
        return ;
    }
    vis[u]=;
    for(int i=;i<=n;i++)     //从小到大去枚举每个点
    {
        if(i!=fa&&f[u][i]&&!vis[i]) //判断是否连接
        {
            dfs(i,u);
            if(bi) return ;   //剪枝
        }
    }
}
int main()
{
    n=read();m=read();
    for(int i=;i<=m;i++)
    {
        u[i]=read();v[i]=read();
        add(u[i],v[i]);add(v[i],u[i]);    //链表存图,tarjan的时候方便
        f[u[i]][v[i]]=;f[v[i]][u[i]]=;  //邻接矩阵存图,选择贪心决策的时候方便从小到大找儿子
    }
    for(int i=;i<=n;i++)                 //tarjan找环
    {
        if(!dfn[i]) tarjan(i,);
    }
    memset(ans,0x3f,sizeof(ans));
    if(m==n-)                            //前60pts
    {
        dfs(,);
        for(int i=;i<=n;i++) printf("%d ",ans[i]);
        return ;
    }
    else                                  //后40pts:基环树
    {
        for(int i=;i<=m;i++)
        {
            if(scc[u[i]]==scc[v[i]])      //只需删除同一联通块里的边
            {
                tot=;bi=;bj=;          //bi表示是否一定不会找到更优解,bj表示是否找到了更优解
                memset(vis,,sizeof(vis));
                f[u[i]][v[i]]=;          //暂时删边,这里用邻接矩阵就比较方便了
                f[v[i]][u[i]]=;
                dfs(,);                 //更新答案
                f[u[i]][v[i]]=;          //记得恢复
                f[v[i]][u[i]]=;
            }
        }
    }
    for(int i=;i<=n;i++) printf("%d ",ans[i]);
    return ;
}