利用反射快速给Model实体赋值使用 Task 简化异步编程 Guid ToString 格式知多少？(GUID 格式) Parallel Programming-实现并行操作的流水线（生产者、消费者） c# 无损高质量压缩图片代码 8种主要排序算法的C#实现（一） 8种主要排序算法的C#实现（二）

试想这样一个业务需求：有一张合同表，由于合同涉及内容比较多所以此表比较庞大，大概有120多个字段。现在合同每一次变更时都需要对合同原始信息进行归档一次，版本号依次递增。那么我们就要新建一张合同历史表，字段跟原合同表一模一样，此外多了一个合同版本号字段。在归档时如何把原始合同信息插入到合同历史表呢？

很容易就能想到的一种解决方法：

insert into 合同历史表（字段1,字段2，字段3…………字段120，版本号） select 字段1,字段2，字段3…………字段120，0 as 版本号 from 合同表 where 合同ID=‘xxxxxxx’

这样当然是能实现我们的功能的，但是看到了吗？由于表的字段太多，导致SQL看起来很不优雅，而且字段之间的对应很容易出问题。联想起之前看过的利用反射给model赋值的例子想出来下面的一个解决方法：

现在假设两个实体class1、class2，class2只比class1多一个字段newid，其它字段一模一样。简单定义如下：

class Class1
    {
        private string id;  

        public string Id
        {
            get { return id; }
            set { id = value; }
        }
        private string name;  

        public string Name
        {
            get { return name; }
            set { name = value; }
        }
        private int age;  

        public int Age
        {
            get { return age; }
            set { age = value; }
        }
        private int num;  

        public int Num
        {
            get { return num; }
            set { num = value; }
        }  

    }

class Class2
    {
        private string newid;  

        public string Newid
        {
            get { return newid; }
            set { newid = value; }
        }  

        private string id;  

        public string Id
        {
            get { return id; }
            set { id = value; }
        }
        private string name;  

        public string Name
        {
            get { return name; }
            set { name = value; }
        }
        private int age;  

        public int Age
        {
            get { return age; }
            set { age = value; }
        }
        private int num;  

        public int Num
        {
            get { return num; }
            set { num = value; }
        }
    }

下面我们给class1赋值，然后通过反射获取class2的属性，循环把class1对应的值赋给class2，遇到class2多出的字段我们手功处理后跳过。简单代码如下：

Class1 c1 = new Class1();
         c1.Id = "001";
         c1.Name = "ben.jiang";
         c1.Num = 712104195;
         c1.Age = 24;  

         Class2 c2 = new Class2();
         Type t2 = typeof(Class2);
         PropertyInfo[] propertys2 = t2.GetProperties();  

         Type t1 = typeof(Class1);
         PropertyInfo[] propertys1 = t1.GetProperties();  

         foreach (PropertyInfo pi in propertys2)
         {
             string name = pi.Name;
             if (name == "Newid")
             {
                 c2.Newid = "newid";
                 continue;
             }  

             object value=t1.GetProperty(name).GetValue(c1, null);
             t2.GetProperty(name).SetValue(c2,value ,null);
         }

这样代码看起来稍微优雅了一些，而且针对不同的字段我们处理起来也方便。

.Net 传统异步编程概述

.NET Framework 提供以下两种执行 I/O 绑定和计算绑定异步操作的标准模式：

异步编程模型 (APM)，在该模型中异步操作由一对 Begin/End 方法（如 FileStream.BeginRead 和 Stream.EndRead）表示。
基于事件的异步模式 (EAP)，在该模式中异步操作由名为“操作名称Async”和“操作名称Completed”的方法/事件对（例如 WebClient.DownloadStringAsync 和 WebClient.DownloadStringCompleted）表示。（EAP 是在 .NET Framework 2.0 版中引入的）。

Task 的优点以及功能

通过使用 Task 对象，可以简化代码并利用以下有用的功能：

在任务启动后，可以随时以任务延续的形式注册回调。
通过使用 ContinueWhenAll 和 ContinueWhenAny 方法或者 WaitAll 方法或 WaitAny 方法，协调多个为了响应 Begin_ 方法而执行的操作。
在同一 Task 对象中封装异步 I/O 绑定和计算绑定操作。
监视 Task 对象的状态。
使用 TaskCompletionSource 将操作的状态封送到 Task 对象。

使用 Task 封装常见的异步编程模式

1、使用 Task 对象封装 APM 异步模式，这种异步模式是 .Net 标准的异步模式之一，也是 .Net 最古老的异步模式，自 .Net 1.0 起就开始出现了，通常由一对 Begin/End 方法同时出现，以 WebRequest 的 BeginGetResponse 与 EndGetResponse 方法为例：

var request = WebRequest.CreateHttp(UrlToTest);
request.Method = "GET";
var requestTask = Task.Factory.FromAsync<WebResponse>(
   request.BeginGetResponse,
   request.EndGetResponse,
   null
);
requestTask.Wait();
var response = requestTask.Result;

2、使用 Task 对象封装 EPM 异步模式，这种模式从 .Net 2.0 开始出现，同时在 Silverlight 中大量出现，这种异步模式以 “操作名称Async” 函数和 “操作名称Completed” 事件成对出现为特征，以 WebClient 的 DownloadStringAsync 方法与 DownLoadStringCompleted 事件为例：

var source = new TaskCompletionSource<string>();
var webClient = new WebClient();
webClient.DownloadStringCompleted += (sender, args) => {
   if (args.Cancelled) {
      source.SetCanceled();
      return;
   }
   if (args.Error != null) {
      source.SetException(args.Error);
      return;
   }
   source.SetResult(args.Result);
};
webClient.DownloadStringAsync(new Uri(UrlToTest, UriKind.Absolute), null);
source.Task.Wait();
var result = source.Task.Result;

3、使用 Task 对象封装其它非标准异步模式，这种模式大量出现在第三方类库中，通常通过一个 Action 参数进行回调，以下面的方法为例：

void AddAsync(int a, int b, Action<int> callback)

封装方法与封装 EPM 异步模式类似：

var source = new TaskCompletionSource<int>();
Action<int> callback = i => source.SetResult(i);
AddAsync(1, 2, callback);
source.Task.Wait();
var result = source.Task.Result;

通过上面的例子可以看出，用 Task 对象对异步操作进行封装之后，异步操作简化了很多，只要调用 Task 的 Wait 方法，可以直接获取异步操作的结果，而不用转到回调函数中进行处理，接下来看一个比较实际的例子。

缓冲查询示例

以 Esri 提供的缓冲查询为例，用户现在地图上选择一个合适的点，按照一定半径查询查询缓冲区，再查询这个缓冲区内相关的建筑物信息，这个例子中，我们需要与服务端进行两次交互：

根据用户选择的点查询出缓冲区；
查询缓冲区内的建筑物信息；

这个例子在 GIS 查询中可以说是非常简单的，也是很典型的， ESRI 的例子中也给出了完整的源代码，这个例子的核心逻辑代码是：

_geometryService = new GeometryService(GeoServerUrl);
_geometryService.BufferCompleted += GeometryService_BufferCompleted;

_queryTask = new QueryTask(QueryTaskUrl);
_queryTask.ExecuteCompleted += QueryTask_ExecuteCompleted;

void MyMap_MouseClick(object sender, Map.MouseEventArgs e) {
   // 部分代码省略， 开始缓冲查询
   _geometryService.BufferAsync(bufferParams);

}

void GeometryService_BufferCompleted(object sender, GraphicsEventArgs args) {
   // 部分代码省略， 获取缓冲查询结果， 开始查询缓冲区内的建筑物信息
   _queryTask.ExecuteAsync(query);
}

void QueryTask_ExecuteCompleted(object sender, QueryEventArgs args) {
   // 将查询结果更新到界面上
}

这只是一个 GIS 开发中很简单的一个查询，上面的代码却将逻辑分散在三个函数中，在实际应用中，与服务端的交互次数会更多，代码的逻辑会分散在更多的函数中，导致代码的可读性以及可维护性降低。如果使用 Task 对象对这些任务进行封装，那么整个逻辑将会简洁很多， GeometryService 和 QueryTask 提供的是 EPM 异步模式，相应的封装方法如上所示，最后，用 Task 封装异步操作之后的代码如下：

void MyMap_MouseClick(object sender, Map.MouseEventArgs e) {
   Task.Factory.StartNew(() => {
      // 省略部分 UI 代码， 开始缓冲查询
      var bufferParams = new BufferParameters() { /* 初始化缓冲查询参数 */};
      var bufferTask = _geometryService.CreateBufferTask()
      // 等待缓冲查询结果
      bufferTask.Wait();
      // 省略更新 UI 的代码， 开始查询缓冲区内的建筑物信息
      var query = new Query() { /* 初始化查询参数 */ };
      var queryExecTask = _queryTask.CreateExecTask(query);
      queryExecTask.Wait();
      // 将查询结果显示在界面上， 代码省略
   });
}

从上面的代码可以看出，使用 Task 对象可以把原本分散在三个函数中的逻辑集中在一个函数中即可完成，代码的可读性、可维护性比原来增加了很多。

Task 能完成的任务远不止这些，比如并行计算、协调多个并发任务等，有兴趣的可以进一步阅读相关的 MSDN 资料。

在日常编程中，Guid是比较常用的，最常见的使用就是如下所示：

string id = Guid.NewGuid().ToString();

这条语句会生成一个新的Guid并转成字符串，如下：

// 10244798-9a34-4245-b1ef-9143f9b1e68a

但是还有一些情况下，我们会有一些细节上的差异，如：

前后有大括号{xxxxxxxx-xxxx-xxxx-xxxx-xxxxxxxxxxxx}
中间没有连字符 xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
前后是圆括号(xxxxxxxx-xxxx-xxxx-xxxx-xxxxxxxxxxxx)

遇到这种情况就比较麻烦了，最常见的一种就是自己把guid生成的字符串解析处理，比如加括号，或者把连字符用空字符替换掉等：

var str = guid.ToString();

var id = "{" + str + "}";
var id2 = str.Replace("-", "");
var id3 = "(" + str + ")";

其实不用这么麻烦的，在ToString的时候，有一个重载的函数：

ToString(String)

通过传入格式化字符串，就可以输出这种类型的guid 字符串了。

示例如下：

var guid = Guid.NewGuid();

// 10244798-9a34-4245-b1ef-9143f9b1e68a
Console.WriteLine(guid.ToString("D"));

// 102447989a344245b1ef9143f9b1e68a
Console.WriteLine(guid.ToString("N"));

// {10244798-9a34-4245-b1ef-9143f9b1e68a}
Console.WriteLine(guid.ToString("B"));

// (10244798-9a34-4245-b1ef-9143f9b1e68a)
Console.WriteLine(guid.ToString("P"));

注意：这里的D，N，B，P是不区分大小写的，如果传入空字符串，则使用的默认的D类型，其它情况都会报异常。

在MSDN中查询到还有一种“X”类型，但是我在.NetFx 3.5下，使用时会弹出异常：

未处理的异常: System.FormatException: 格式字符串只能是“D”、“d”、“N”、“n ”、“P”、“p”、“B”或“b”。
在 System.Guid.ToString(String format, IFormatProvider provider)

本文介绍如何使用C#实现并行执行的流水线（生产者消费者）：

1.流水线示意图

2.实现并行流水线

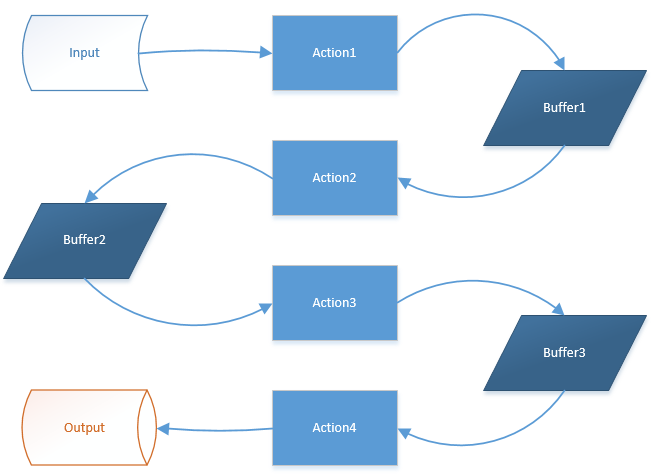
一、流水线示意图

上图演示了流水线，action1接收input，然后产生结果保存在buffer1中，action2读取buffer1中由action1产生的数据，以此类推指导action4完成产生Output。

以上也是典型的生产者消费者模式。

上面的模式如果使用普通常规的串行执行是很简单的，按部就班按照流程图一步一步执行即可。如果为了提高效率，想使用并行执行，也就是说生产者和消费者同时并行执行，该怎么办么？

二、实现并行流水线

2.1 代码
class PiplelineDemo
    {
        private int seed;
        public PiplelineDemo()
        {
            seed = 10;
        }

        public void Action1(BlockingCollection<string> output)
        {
            try
            {
                for (var i = 0; i < seed; i++)
                {
                    output.Add(i.ToString());//initialize data to buffer1
                }
            }
            finally
            {
                output.CompleteAdding();
            }
        }

        public void Action2(BlockingCollection<string> input, BlockingCollection<string> output)
        {
            try
            {
                foreach (var item in input.GetConsumingEnumerable())
                {
                    var itemToInt = int.Parse(item);
                    output.Add((itemToInt * itemToInt).ToString());// add new data to buffer2
                }
            }
            finally
            {
                output.CompleteAdding();
            }
        }

        public void Action3(BlockingCollection<string> input, BlockingCollection<string> output)
        {
            try
            {
                foreach (var item in input.GetConsumingEnumerable())
                {
                    output.Add(item);//set data into buffer3
                }
            }
            finally
            {
                output.CompleteAdding();
            }
        }

        public void Pipeline()
        {
            var buffer1 = new BlockingCollection<string>(seed);
            var buffer2 = new BlockingCollection<string>(seed);
            var buffer3 = new BlockingCollection<string>(seed);
            var taskFactory = new TaskFactory(TaskCreationOptions.LongRunning, TaskContinuationOptions.None);
            var stage1 = taskFactory.StartNew(() => Action1(buffer1));
            var stage2 = taskFactory.StartNew(() => Action2(buffer1, buffer2));
            var stage3 = taskFactory.StartNew(() => Action3(buffer2, buffer3));

            Task.WaitAll(stage1, stage2, stage3);
            foreach(var item in buffer3.GetConsumingEnumerable())//print data in buffer3
            {
                Console.WriteLine(item);
            }
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            new PiplelineDemo().Pipeline();
            Console.Read();
        }
    }
2.2 运行结果

预期打印出了0-9自我相乘的结果。

2.3 代码解释

代码本身的逻辑和本文开始的流程图是一一对应的。

BlockingCollection<T>是.Net里面的一个线程安全集合。实现了IProducerConsumerCollection<T>.

Add方法：将元素加入集合

CompleteAdding方法：告诉消费者，在当调用该方法之前的元素处理完之后就不要再等待处理了，可以结束处理了。这个非常重要，一定要执行，所以放在finally中（就算exception也要执行）

GetConsumingEnumberable，给消费者返回一个可以便利的集合

在CSDN上看到了一个压缩算法：http://blog.csdn.net/qq_16542775/article/details/51792149

进过测试这个算法，发现，将原始图像的大小进行对半处理，然后迭代跳转压缩质量参数，可以得到不错的效果。
/// <summary>
/// 无损压缩图片
/// </summary>
/// <param name="sFile">原图片地址</param>
/// <param name="dFile">压缩后保存图片地址</param>
/// <param name="flag">压缩质量（数字越小压缩率越高）1-100</param>
/// <param name="size">压缩后图片的最大大小</param>
/// <param name="sfsc">是否是第一次调用</param>
/// <returns></returns>
public static bool CompressImage(string sFile, string dFile, int flag = 90, int size = 300, bool sfsc = true)
{
//如果是第一次调用，原始图像的大小小于要压缩的大小，则直接复制文件，并且返回true
    FileInfo firstFileInfo = new FileInfo(sFile);
    if (sfsc == true && firstFileInfo.Length < size * 1024)
    {
        firstFileInfo.CopyTo(dFile);
        return true;
    }
    Image iSource = Image.FromFile(sFile);
    ImageFormat tFormat = iSource.RawFormat;
int dHeight = iSource.Height / 2;
    int dWidth = iSource.Width / 2;
    int sW = 0, sH = 0;
    //按比例缩放
    Size tem_size = new Size(iSource.Width, iSource.Height);
    if (tem_size.Width > dHeight || tem_size.Width > dWidth)
    {
        if ((tem_size.Width * dHeight) > (tem_size.Width * dWidth))
        {
            sW = dWidth;
            sH = (dWidth * tem_size.Height) / tem_size.Width;
        }
        else
        {
            sH = dHeight;
            sW = (tem_size.Width * dHeight) / tem_size.Height;
        }
    }
    else
    {
        sW = tem_size.Width;
        sH = tem_size.Height;
    }

    Bitmap ob = new Bitmap(dWidth, dHeight);
    Graphics g = Graphics.FromImage(ob);

    g.Clear(Color.WhiteSmoke);
    g.CompositingQuality = System.Drawing.Drawing2D.CompositingQuality.HighQuality;
    g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.HighQuality;
    g.InterpolationMode = System.Drawing.Drawing2D.InterpolationMode.HighQualityBicubic;

    g.DrawImage(iSource, new Rectangle((dWidth - sW) / 2, (dHeight - sH) / 2, sW, sH), 0, 0, iSource.Width, iSource.Height, GraphicsUnit.Pixel);

    g.Dispose();

    //以下代码为保存图片时，设置压缩质量
    EncoderParameters ep = new EncoderParameters();
    long[] qy = new long[1];
    qy[0] = flag;//设置压缩的比例1-100
    EncoderParameter eParam = new EncoderParameter(System.Drawing.Imaging.Encoder.Quality, qy);
    ep.Param[0] = eParam;

    try
    {
        ImageCodecInfo[] arrayICI = ImageCodecInfo.GetImageEncoders();
        ImageCodecInfo jpegICIinfo = null;
        for (int x = 0; x < arrayICI.Length; x++)
        {
            if (arrayICI[x].FormatDescription.Equals("JPEG"))
            {
                jpegICIinfo = arrayICI[x];
                break;
            }
        }
        if (jpegICIinfo != null)
        {
            ob.Save(dFile, jpegICIinfo, ep);//dFile是压缩后的新路径
            FileInfo fi = new FileInfo(dFile);
            if (fi.Length > 1024 * size)
            {
                flag = flag - 10;
                CompressImage(sFile, dFile, flag, size, false);
            }
        }
        else
        {
            ob.Save(dFile, tFormat);
        }
        return true;
    }
    catch
    {
        return false;
    }
    finally
    {
        iSource.Dispose();
        ob.Dispose();
    }
}
简介

排序算法是我们编程中遇到的最多的算法。目前主流的算法有8种。

平均时间复杂度从高到低依次是：

冒泡排序（o(n²)），选择排序（o(n²)），插入排序（o(n²)），堆排序（o(nlogn)），

归并排序（o(nlogn)），快速排序（o(nlogn)），希尔排序（o(n^1.25)），基数排序（o(n)）

这些平均时间复杂度是参照维基百科排序算法罗列的。

是计算的理论平均值，并不意味着你的代码实现能达到这样的程度。

例如希尔排序，时间复杂度是由选择的步长决定的。基数排序时间复杂度最小，

但我实现的基数排序的速度并不是最快的，后面的结果测试图可以看到。

本文代码实现使用的数据源类型为IList<int>，这样可以兼容int[]和List<int>(虽然int[]有ToList()，

List<int>有ToArray()，哈哈！)。

选择排序

选择排序是我觉得最简单暴力的排序方式了。

以前刚接触排序算法的时候，感觉算法太多搞不清，唯独记得选择排序的做法及实现。

原理：找出参与排序的数组最大值，放到末尾（或找到最小值放到开头）维基入口

实现如下：
public static void SelectSort(IList<int> data)
        {
            for (int i = 0; i < data.Count - 1; i++)
            {
                int min = i;
                int temp = data[i];
                for (int j = i + 1; j < data.Count; j++)
                {
                    if (data[j] < temp)
                    {
                        min = j;
                        temp = data[j];
                    }
                }
                if (min != i)
                    Swap(data, min, i);
            }
        }
过程解析：将剩余数组的最小数交换到开头。

冒泡排序

冒泡排序是笔试面试经常考的内容，虽然它是这些算法里排序速度最慢的（汗），后面有测试为证。

原理：从头开始，每一个元素和它的下一个元素比较，如果它大，就将它与比较的元素交换，否则不动。

这意味着，大的元素总是在向后慢慢移动直到遇到比它更大的元素。所以每一轮交换完成都能将最大值

冒到最后。维基入口

实现如下：
public static void BubbleSort(IList<int> data)
        {
            for (int i = data.Count - 1; i > 0; i--)
            {
                for (int j = 0; j < i; j++)
                {
                    if (data[j] > data[j + 1])
                        Swap(data, j, j + 1);
                }
            }
        }
过程解析：中需要注意的是j<i，每轮冒完泡必然会将最大值排到数组末尾，所以需要排序的数应该是在减少的。

很多网上版本每轮冒完泡后依然还是将所有的数进行第二轮冒泡即j<data.Count-1，这样会增加比较次数。

通过标识提升冒泡排序

在维基上看到，可以通过添加标识来分辨剩余的数是否已经有序来减少比较次数。感觉很有意思，可以试试。

实现如下：
public static void BubbleSortImprovedWithFlag(IList<int> data)
        {
            bool flag;
            for (int i = data.Count - 1; i > 0; i--)
            {
                flag = true;
                for (int j = 0; j < i; j++)
                {
                    if (data[j] > data[j + 1])
                    {
                        Swap(data, j, j + 1);
                        flag = false;
                    }
                }
                if (flag) break;
            }
        }
过程解析：发现某轮冒泡没有任何数进行交换（即已经有序），就跳出排序。

我起初也以为这个方法是应该有不错效果的，可是实际测试结果并不如想的那样。和未优化耗费时间一样（对于随机数列）。

由果推因，那么应该是冒泡排序对于随机数列，当剩余数列有序的时候，也没几个数要排列了！？

不过如果已经是有序数列或者部分有序的话，这个冒泡方法将会提升很大速度。

鸡尾酒排序（来回排序）

对冒泡排序进行更大的优化

冒泡排序只是单向冒泡，而鸡尾酒来回反复双向冒泡。

原理：自左向右将大数冒到末尾，然后将剩余数列再自右向左将小数冒到开头，如此循环往复。维基入口

实现如下：
public static void BubbleCocktailSort(IList<int> data)
        {
            bool flag;
            int m = 0, n = 0;
            for (int i = data.Count - 1; i > 0; i--)
            {
                flag = true;
                if (i % 2 == 0)
                {
                    for (int j = n; j < data.Count - 1 - m; j++)
                    {
                        if (data[j] > data[j + 1])
                        {
                            Swap(data, j, j + 1);
                            flag = false;
                        }
                    }
                    if (flag) break;
                    m++;
                }
                else
                {
                    for (int k = data.Count - 1 - m; k > n; k--)
                    {
                        if (data[k] < data[k - 1])
                        {
                            Swap(data, k, k - 1);
                            flag = false;
                        }
                    }
                    if (flag) break;
                    n++;
                }
            }
        }
过程解析：分析第i轮冒泡，i是偶数则将剩余数列最大值向右冒泡至末尾，是奇数则将剩余数列最小值

向左冒泡至开头。对于剩余数列，n为始，data.Count-1-m为末。

来回冒泡比单向冒泡：对于随机数列，更容易得到有序的剩余数列。因此这里使用标识将会提升的更加明显。

插入排序

插入排序是一种对于有序数列高效的排序。非常聪明的排序。只是对于随机数列，效率一般，交换的频率高。

原理：通过构建有序数列，将未排序的数从后向前比较，找到合适位置并插入。维基入口

第一个数当作有序数列。

实现如下：
public static void InsertSort(IList<int> data)
        {
            int temp;
            for (int i = 1; i < data.Count; i++)
            {
                temp = data[i];
                for (int j = i - 1; j >= 0; j--)
                {
                    if (data[j] > temp)
                    {
                        data[j + 1] = data[j];
                        if (j == 0)
                        {
                            data[0] = temp;
                            break;
                        }
                    }
                    else
                    {
                        data[j + 1] = temp;
                        break;
                    }
                }
            }
        }
过程解析：将要排序的数（索引为i）存储起来，向前查找合适位置j+1，将i-1到j+1的元素依次向后

移动一位，空出j+1，然后将之前存储的值放在这个位置。

这个方法写的不如维基上的简洁清晰，由于合适位置是j+1所以多出了对j==0的判断，但实际效率影响无差别。

建议比照维基和我写的排序，自行选择。

二分查找法优化插入排序

插入排序主要工作是在有序的数列中对要排序的数查找合适的位置，而查找里面经典的二分查找法正可以适用。

原理：通过二分查找法的方式找到一个位置索引。当要排序的数插入这个位置时，大于前一个数，小于后一个数。

实现如下：
public static void InsertSortImprovedWithBinarySearch(IList<int> data)
        {
            int temp;
            int tempIndex;
            for (int i = 1; i < data.Count; i++)
            {
                temp = data[i];
                tempIndex = BinarySearchForInsertSort(data, 0, i, i);
                for (int j = i - 1; j >= tempIndex; j--)
                {
                    data[j + 1] = data[j];
                }
                data[tempIndex] = temp;
            }
        }

        public static int BinarySearchForInsertSort(IList<int> data, int low, int high, int key)
        {
            if (low >= data.Count - 1)
                return data.Count - 1;
            if (high <= 0)
                return 0;
            int mid = (low + high) / 2;
            if (mid == key) return mid;
            if (data[key] > data[mid])
            {
                if (data[key] < data[mid + 1])
                    return mid + 1;
                return BinarySearchForInsertSort(data, mid + 1, high, key);
            }
            else  // data[key] <= data[mid]
            {
                if (mid - 1 < 0) return 0;
                if (data[key] > data[mid - 1])
                    return mid;
                return BinarySearchForInsertSort(data, low, mid - 1, key);
            }
        }
过程解析：需要注意的是二分查找方法实现中high-low==1的时候mid==low，所以需要33行

mid-1<0即mid==0的判断，否则下行会索引越界。

快速排序

快速排序是一种有效比较较多的高效排序。它包含了“分而治之”以及“哨兵”的思想。

原理：从数列中挑选一个数作为“哨兵”，使比它小的放在它的左侧，比它大的放在它的右侧。将要排序是数列递归地分割到

最小数列，每次都让分割出的数列符合“哨兵”的规则，自然就将数列变得有序。维基入口

实现如下：
public static void QuickSortStrict(IList<int> data)
        {
            QuickSortStrict(data, 0, data.Count - 1);
        }

        public static void QuickSortStrict(IList<int> data, int low, int high)
        {
            if (low >= high) return;
            int temp = data[low];
            int i = low + 1, j = high;
            while (true)
            {
                while (data[j] > temp) j--;
                while (data[i] < temp && i < j) i++;
                if (i >= j) break;
                Swap(data, i, j);
                i++; j--;
            }
            if (j != low)
                Swap(data, low, j);
            QuickSortStrict(data, j + 1, high);
            QuickSortStrict(data, low, j - 1);
        }
过程解析：取的哨兵是数列的第一个值，然后从第二个和末尾同时查找，左侧要显示的是小于哨兵的值，

所以要找到不小于的i，右侧要显示的是大于哨兵的值，所以要找到不大于的j。将找到的i和j的数交换，

这样可以减少交换次数。i>=j时，数列全部查找了一遍，而不符合条件j必然是在小的那一边，而哨兵

是第一个数，位置本应是小于自己的数。所以将哨兵与j交换，使符合“哨兵”的规则。

这个版本的缺点在于如果是有序数列排序的话，递归次数会很可怕的。

另一个版本

这是维基上的一个C#版本，我觉得很有意思。这个版本并没有严格符合“哨兵”的规则。但却将“分而治之”

以及“哨兵”思想融入其中，代码简洁。

实现如下：
public static void QuickSortRelax(IList<int> data)
        {
            QuickSortRelax(data, 0, data.Count - 1);
        }

        public static void QuickSortRelax(IList<int> data, int low, int high)
        {
            if (low >= high) return;
            int temp = data[(low + high) / 2];
            int i = low - 1, j = high + 1;
            while (true)
            {
                while (data[++i] < temp) ;
                while (data[--j] > temp) ;
                if (i >= j) break;
                Swap(data, i, j);
            }
            QuickSortRelax(data, j + 1, high);
            QuickSortRelax(data, low, i - 1);
        }
过程解析：取的哨兵是数列中间的数。将数列分成两波，左侧小于等于哨兵，右侧大于等于哨兵。

也就是说，哨兵不一定处于两波数的中间。虽然哨兵不在中间，但不妨碍“哨兵”的思想的实现。所以

这个实现也可以达到快速排序的效果。但却造成了每次递归完成，要排序的数列数总和没有减少（除非i==j）。

针对这个版本的缺点，我进行了优化

实现如下：
public static void QuickSortRelaxImproved(IList<int> data)
        {
            QuickSortRelaxImproved(data, 0, data.Count - 1);
        }

        public static void QuickSortRelaxImproved(IList<int> data, int low, int high)
        {
            if (low >= high) return;
            int temp = data[(low + high) / 2];
            int i = low - 1, j = high + 1;
            int index = (low + high) / 2;
            while (true)
            {
                while (data[++i] < temp) ;
                while (data[--j] > temp) ;
                if (i >= j) break;
                Swap(data, i, j);
                if (i == index) index = j;
                else if (j == index) index = i;
            }
            if (j == i)
            {
                QuickSortRelaxImproved(data, j + 1, high);
                QuickSortRelaxImproved(data, low, i - 1);
            }
            else //i-j==1
            {
                if (index >= i)
                {
                    if (index != i)
                        Swap(data, index, i);
                    QuickSortRelaxImproved(data, i + 1, high);
                    QuickSortRelaxImproved(data, low, i - 1);
                }
                else //index < i
                {
                    if (index != j)
                        Swap(data, index, j);
                    QuickSortRelaxImproved(data, j + 1, high);
                    QuickSortRelaxImproved(data, low, j - 1);
                }
            }
        }
public static void QuickSortRelaxImproved(IList<int> data)
        {
            QuickSortRelaxImproved(data, 0, data.Count - 1);
        }

        public static void QuickSortRelaxImproved(IList<int> data, int low, int high)
        {
            if (low >= high) return;
            int temp = data[(low + high) / 2];
            int i = low - 1, j = high + 1;
            int index = (low + high) / 2;
            while (true)
            {
                while (data[++i] < temp) ;
                while (data[--j] > temp) ;
                if (i >= j) break;
                Swap(data, i, j);
                if (i == index) index = j;
                else if (j == index) index = i;
            }
            if (j == i)
            {
                QuickSortRelaxImproved(data, j + 1, high);
                QuickSortRelaxImproved(data, low, i - 1);
            }
            else //i-j==1
            {
                if (index >= i)
                {
                    if (index != i)
                        Swap(data, index, i);
                    QuickSortRelaxImproved(data, i + 1, high);
                    QuickSortRelaxImproved(data, low, i - 1);
                }
                else //index < i
                {
                    if (index != j)
                        Swap(data, index, j);
                    QuickSortRelaxImproved(data, j + 1, high);
                    QuickSortRelaxImproved(data, low, j - 1);
                }
            }
        }
过程解析：定义了一个变量Index，来跟踪哨兵的位置。发现哨兵最后在小于自己的那堆，

那就与j交换，否则与i交换。达到每次递归都能减少要排序的数列数总和的目的。

归并排序

归并排序也是采用“分而治之”的方式。刚发现分治法是一种算法范式，我还一直以为是一种需要意会的思想呢。

不好意思了，孤陋寡闻了，哈哈！

原理：将两个有序的数列，通过比较，合并为一个有序数列。维基入口

为方便理解，此处实现用了List<int>的一些方法，随后有IList<int>版本。

实现如下：
public static List<int> MergeSortOnlyList(List<int> data, int low, int high)
        {
            if (low == high)
                return new List<int> { data[low] };
            List<int> mergeData = new List<int>();
            int mid = (low + high) / 2;
            List<int> leftData = MergeSortOnlyList(data, low, mid);
            List<int> rightData = MergeSortOnlyList(data, mid + 1, high);
            int i = 0, j = 0;
            while (true)
            {
                if (leftData[i] < rightData[j])
                {
                    mergeData.Add(leftData[i]);
                    if (++i == leftData.Count)
                    {
                        mergeData.AddRange(rightData.GetRange(j, rightData.Count - j));
                        break;
                    }
                }
                else
                {
                    mergeData.Add(rightData[j]);
                    if (++j == rightData.Count)
                    {
                        mergeData.AddRange(leftData.GetRange(i, leftData.Count - i));
                        break;
                    }
                }
            }
            return mergeData;
        }

        public static List<int> MergeSortOnlyList(List<int> data)
        {
            data = MergeSortOnlyList(data, 0, data.Count - 1);  //不会改变外部引用 参照C#参数传递
            return data;
        }
过程解析：将数列分为两部分，分别得到两部分数列的有序版本，然后逐个比较，将比较出的小数逐个放进

新的空数列中。当一个数列放完后，将另一个数列剩余数全部放进去。

IList<int>版本

实现如下：
public static IList<int> MergeSort(IList<int> data)
        {
            data = MergeSort(data, 0, data.Count - 1);
            return data;
        }

        public static IList<int> MergeSort(IList<int> data, int low, int high)
        {
            int length = high - low + 1;
            IList<int> mergeData = NewInstance(data, length);
            if (low == high)
            {
                mergeData[0] = data[low];
                return mergeData;
            }
            int mid = (low + high) / 2;
            IList<int> leftData = MergeSort(data, low, mid);
            IList<int> rightData = MergeSort(data, mid + 1, high);
            int i = 0, j = 0;
            while (true)
            {
                if (leftData[i] < rightData[j])
                {
                    mergeData[i + j] = leftData[i++]; //不能使用Add,Array Length不可变
                    if (i == leftData.Count)
                    {
                        int rightLeft = rightData.Count - j;
                        for (int m = 0; m < rightLeft; m++)
                        {
                            mergeData[i + j] = rightData[j++];
                        }
                        break;
                    }
                }
                else
                {
                    mergeData[i + j] = rightData[j++];
                    if (j == rightData.Count)
                    {
                        int leftleft = leftData.Count - i;
                        for (int n = 0; n < leftleft; n++)
                        {
                            mergeData[i + j] = leftData[i++];
                        }
                        break;
                    }
                }
            }
            return mergeData;

        }
过程原理与上个一样，此处就不赘述了。

堆排序

堆排序是根据堆这种数据结构设计的一种算法。堆的特性：父节点的值总是小于（或大于）它的子节点。近似二叉树。

原理：将数列构建为最大堆数列（即父节点总是最大值），将最大值（即根节点）交换到数列末尾。这样要排序的数列数总和减少，

同时根节点不再是最大值，调整最大堆数列。如此重复，最后得到有序数列。维基入口有趣的演示

实现准备：如何将数列构造为堆——父节点i的左子节点为2i+1，右子节点为2i+2。节点i的父节点为floor((i-1)/2)。

实现如下（这个实现判断和临时变量使用太多，导致效率低，评论中@小城故事提出了更好的实现）：
public static void HeapSort(IList<int> data)
        {
            BuildMaxHeapify(data);
            int j = data.Count;
            for (int i = 0; i < j; )
            {
                Swap(data, i, --j);
                if (j - 2 < 0)  //只剩下1个数 j代表余下要排列的数的个数
                    break;
                int k = 0;
                while (true)
                {
                    if (k > (j - 2) / 2) break;  //即：k > ((j-1)-1)/2 超出最后一个父节点的位置
                    else
                    {
                        int temp = k;
                        k = ReSortMaxBranch(data, k, 2 * k + 1, 2 * k + 2, j - 1);
                        if (temp == k) break;
                    }
                }
            }
        }

        public static void BuildMaxHeapify(IList<int> data)
        {
            for (int i = data.Count / 2 - 1; i >= 0; i--)  //(data.Count-1)-1)/2为数列最大父节点索引
            {
                int temp = i;
                temp = ReSortMaxBranch(data, i, 2 * i + 1, 2 * i + 2, data.Count - 1);
                if (temp != i)
                {
                    int k = i;
                    while (k != temp && temp <= data.Count / 2 - 1)
                    {
                        k = temp;
                        temp = ReSortMaxBranch(data, temp, 2 * temp + 1, 2 * temp + 2, data.Count - 1);
                    }
                }
            }
        }

        public static int ReSortMaxBranch(IList<int> data, int maxIndex, int left, int right, int lastIndex)
        {
            int temp;
            if (right > lastIndex)  //父节点只有一个子节点
                temp = left;
            else
            {
                if (data[left] > data[right])
                    temp = left;
                else temp = right;
            }

            if (data[maxIndex] < data[temp])
                Swap(data, maxIndex, temp);
            else temp = maxIndex;
            return temp;
        }
过程解析：BuildMaxHeapify为排序前构建的最大堆数列方法，主要内容为从最后一个父节点开始往前将每个三角组合

（即父节点与它的两个子节点）符合父节点值最大的规则。ReSortMaxBranch为将三角调整为父节点值最大，

并返回该值之前的索引，用来判断是否进行了交换，以及原来的父节点值交换到了什么位置。在HeapSort里首先

构建了最大堆数列，然后将根节点交换到末尾，根节点不是最大值了，在while语句中对最大堆数列进行调整。

插曲：自从看了Martin Fowler大师《重构》第三版，我发现我更不喜欢写注释了。每次都想着尽量让方法的名字更贴切，

即使会造成方法的名字很长很丑。这算不算曲解了大师的意思啊！？上面的代码注释都是写博客的时候现加的（源代码很干净的。汗!）。

希尔排序

希尔排序是插入排序的一种更高效的改进版本。

在前面介绍的插入排序，我们知道1.它对有序数列排序的效率是非常高的 2.要排序的数向前移动是一步步进行的导致插入排序效率低。

希尔排序正是利用第一点，改善第二点，达到更理想的效果。

原理：通过奇妙的步长，插入排序间隔步长的元素，随后逐渐缩短步长至1，实现数列的插入排序。维基入口

疑问：可以想象到排序间隔步长的数，会逐渐让数列变得有序，提升最后步长为1时标准插入排序的效率。在维基上看到这么

一句话“可能希尔排序最重要的地方在于当用较小步长排序后，以前用的较大步长仍然是有序的”注意用词是‘可能’。我的疑问是

这是个正确的命题吗？如何证明呢？看维基上也是由果推因，说是如果不是这样，就不会排序那么快了。可这我感觉还是太牵强了，

哪位大哥发现相关资料，希望能分享出来，不胜感激。

实现如下：
public static void ShellSortCorrect(IList<int> data)
        {
            int temp;
            for (int gap = data.Count / 2; gap > 0; gap /= 2)
            {
                for (int i = gap; i < data.Count; i++)      // i+ = gap 改为了 i++
                {
                    temp = data[i];
                    for (int j = i - gap; j >= 0; j -= gap)
                    {
                        if (data[j] > temp)
                        {
                            data[j + gap] = data[j];
                            if (j == 0)
                            {
                                data[j] = temp;
                                break;
                            }
                        }
                        else
                        {
                            data[j + gap] = temp;
                            break;
                        }
                    }
                }
            }
        }
基数排序

基数排序是一种非比较型整数排序。

“非比较型”是什么意思呢？因为它内部使用的是桶排序，而桶排序是非比较型排序。

这里就要说说桶排序了。一个非常有意思的排序。

桶排序

原理：取一定数量（数列中的最大值）的编好序号的桶，将数列每个数放进编号为它的桶里，然后将不是空的桶依次倒出来，

就组成有序数列了。维基入口

好吧！聪明的人一眼就看出桶排序的破绽了。假设只有两个数1,10000，岂不是要一万个桶！？这确实是个问题啊！我也

没想出解决办法。我起初也以为桶排序就是一个通过牺牲空间来换取时间的排序算法，它不需要比较，所以是非比较型算法。

但看了有趣的演示的桶排序后，发现世界之大，你没有解决，不代表别人没解决，睿智的人总是很多。

1，9999的桶排序实现：new Int[2];总共有两个数，得出最大数9999的位数4，取10的4次幂即10000作为分母，

要排序的数（1或9999）作为分子，并乘以数列总数2，即1*2/10000,9999*2/10000得到各自的位置0,1，完成排序。

如果是1,10000进行排序的话，上面的做法就需要稍微加一些处理——发现最大数是10的n次幂，就将它作为分母，并

放在数列末尾就好了。

如果是9999,10000进行排序的话，那就需要二维数组了，两个都在位置1，位置0没数。这个时候就需要在放

入每个位置时采用其它排序（比如插入排序）办法对这个位置的多个数排序了。

为基数排序做个过渡，我这里实现了一个个位数桶排序

涉及到了当重复的数出现的处理。

实现如下：
public static void BucketSortOnlyUnitDigit(IList<int> data)
        {
            int[] indexCounter = new int[10];
            for (int i = 0; i < data.Count; i++)
            {
                indexCounter[data[i]]++;
            }
            int[] indexBegin = new int[10];
            for (int i = 1; i < 10; i++)
            {
                indexBegin[i] = indexBegin[i-1]+ indexCounter[i-1];
            }
            IList<int> tempList = NewInstance(data, data.Count);
            for (int i = 0; i < data.Count; i++)
            {
                int number = data[i];
                tempList[indexBegin[number]++] = data[i];
            }
            data = tempList;
        }
过程解析：indexCounter进行对每个数出现的频率的统计。indexBegin存储每个数的起始索引。

比如 1 1 2，indexCounter统计到0个0,2个1,1个2。indexBegin计算出0,1,2的起始索引分别为

0,0,2。当1个1已取出排序，那索引将+1,变为0,1,2。这样就通过提前给重复的数空出位置，解决了

重复的数出现的问题。当然，你也可以考虑用二维数组来解决重复。

下面继续基数排序。

基数排序原理：将整数按位数切割成不同的数字，然后按每个位数分别比较。

取得最大数的位数，从低位开始，每个位上进行桶排序。

实现如下：
public static IList<int> RadixSort(IList<int> data)
        {
            int max = data[0];
            for (int i = 1; i < data.Count; i++)
            {
                if (data[i] > max)
                    max = data[i];
            }
            int digit = 1;
            while (max / 10 != 0)
            {
                digit++;
                max /= 10;
            }
            for (int i = 0; i < digit; i++)
            {
                int[] indexCounter = new int[10];
                IList<int> tempList = NewInstance(data, data.Count);
                for (int j = 0; j < data.Count; j++)
                {
                    int number = (data[j] % Convert.ToInt32(Math.Pow(10, i + 1))) / Convert.ToInt32(Math.Pow(10, i));  //得出i+1位上的数
                    indexCounter[number]++;
                }
                int[] indexBegin = new int[10];
                for (int k = 1; k < 10; k++)
                {
                    indexBegin[k] = indexBegin[k - 1] + indexCounter[k - 1];
                }
                for (int k = 0; k < data.Count; k++)
                {
                    int number = (data[k] % Convert.ToInt32(Math.Pow(10, i + 1))) / Convert.ToInt32(Math.Pow(10, i));
                    tempList[indexBegin[number]++] = data[k];
                }
                data = tempList;
            }
            return data;
        }
过程解析：得出最大数的位数，从低位开始桶排序。我写的这个实现代码并不简洁，但逻辑更清晰。

后面测试的时候我们就会发现，按理来说这个实现也还行吧！但并不如想象的那么快！

循环的次数太多？（统计频率n次+9次计算+n次放到新的数组）*位数。

创建的新实例太多？(new int[10]两次+NewInstance is反射判断创建实例+new int[n])*位数

测试比较

添加随机数组，数组有序校验，微软Linq排序

代码如下：
public static int[] RandomSet(int length, int max)
        {
            int[] result = new int[length];
            Random rand = new Random();
            for (int i = 0; i < result.Length; i++)
            {
                result[i] = rand.Next(max);
            }
            return result;
        }

        public static bool IsAscOrdered(IList<int> data)
        {
            bool flag = true;
            for (int i = 0; i < data.Count - 1; i++)
            {
                if (data[i] > data[i + 1])
                    flag = false;
            }
            return flag;
        }

        public static void TestMicrosoft(IList<int> data)
        {
            Stopwatch stopwatch = new Stopwatch();
            stopwatch.Start();
            List<int> result = data.OrderBy(a => a).ToList();
            stopwatch.Stop();
            string methodName = "TestMicrosoft";
            int length = methodName.Length;
            for (int i = 0; i < 40 - length; i++)
            {
                methodName += " ";
            }
            Console.WriteLine(methodName +
                "  IsAscOrdered:" + IsAscOrdered(result) + "  Time:" + stopwatch.Elapsed.TotalSeconds);

        }
测试主体如下：
static void Main(string[] args)
        {
            int[] aa = RandomSet(50000, 99999);
            //int[] aa = OrderedSet(5000);
            Console.WriteLine("Array Length:" + aa.Length);
            RunTheMethod((Action<IList<int>>)SelectSort, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)BubbleSort, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)BubbleSortImprovedWithFlag, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)BubbleCocktailSort, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)InsertSort, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)InsertSortImprovedWithBinarySearch, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)QuickSortStrict, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)QuickSortRelax, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)QuickSortRelaxImproved, aa.Clone() as int[]);
            RunTheMethod((Func<IList<int>, IList<int>>)MergeSort, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)ShellSort, aa.Clone() as int[]);
            RunTheMethod((Func<IList<int>, IList<int>>)RadixSort, aa.Clone() as int[]);
            RunTheMethod((Action<IList<int>>)HeapSort, aa.Clone() as int[]);
            TestMicrosoft(aa.Clone() as int[]);
            Console.Read();
        }

        public static void RunTheMethod(Func<IList<int>, IList<int>> method, IList<int> data)
        {
            Stopwatch stopwatch = new Stopwatch();
            stopwatch.Start();
            IList<int> result = method(data);
            stopwatch.Stop();
            string methodName = method.Method.Name;
            int length = methodName.Length;
            for (int i = 0; i < 40 - length; i++)
            {
                methodName += " ";
            }
            Console.WriteLine(methodName +
                "  IsAscOrdered:" + IsAscOrdered(result) + "  Time:" + stopwatch.Elapsed.TotalSeconds);
        }

        public static void RunTheMethod(Action<IList<int>> method, IList<int> data)
        {
            Stopwatch stopwatch = new Stopwatch();
            stopwatch.Start();
            method(data);
            stopwatch.Stop();
            string methodName = method.Method.Name;
            int length = methodName.Length;
            for (int i = 0; i < 40 - length; i++)
            {
                methodName += " ";
            }
            Console.WriteLine(methodName +
                "  IsAscOrdered:" + IsAscOrdered(data) + "  Time:" + stopwatch.Elapsed.TotalSeconds);
        }
剩余代码折叠在此处
public static void Swap(IList<int> data, int a, int b)
        {
            int temp = data[a];
            data[a] = data[b];
            data[b] = temp;
        }

        public static int[] OrderedSet(int length)
        {
            int[] result = new int[length];
            for (int i = 0; i < length; i++)
            {
                result[i] = i;
            }
            return result;
        }

        public static IList<int> NewInstance(IList<int> data, int length)
        {
            IList<int> instance;
            if (data is Array)
            {
                instance = new int[length];
            }
            else
            {
                instance = new List<int>(length);
                for (int n = 0; n < length; n++)
                {
                    instance.Add(0);  // 初始添加
                }
            }
            return instance;
        }