【数论分块】bzoj2956: 模积和

数论分块并不精通……第一次调了一个多小时才搞到60pts；因为不会处理i==j的情况，只能枚举了……

Description

$\sum_{i=1}^{n}\sum_{j=1 \land i \not = j}^{m}(n\ mod\ i)(m\ mod\ j)$

Input

第一行两个数n,m。

Output

一个整数表示答案mod 19940417的值

Sample Input

3 4

Sample Output

1

样例说明

答案为(3 mod 1)*(4 mod 2)+(3 mod 1) * (4 mod 3)+(3 mod 1) * (4 mod 4) + (3 mod 2) * (4 mod 1) + (3 mod 2) * (4 mod 3) + (3 mod 2) * (4 mod 4) + (3 mod 3) * (4 mod 1) + (3 mod 3) * (4 mod 2) + (3 mod 3) * (4 mod 4) = 1

数据规模和约定

30%: n,m <= 1000

60%: n,m <= 10^6

100% n,m <= 10^9

---

题目分析

我们有

$原式=\sum_{i=1}^{n}\sum_{j=1}^{m}(n-{\left \lfloor \frac{n}{i} \right \rfloor}i)(m-{\left \lfloor \frac{m}{j} \right \rfloor}j)-\sum_{i=1}^{min(n,m)}(n-{\left \lfloor \frac{n}{i} \right \rfloor}i)(m-{\left \lfloor \frac{m}{i} \right \rfloor}i)$

$=\sum_{i=1}^{n}(n-{\left \lfloor \frac{n}{i} \right \rfloor}i)\sum_{j=1}^{m}(m-{\left \lfloor \frac{m}{j} \right \rfloor}j)-\sum_{i=1}^{min(n,m)}(nm+{\left \lfloor \frac{n}{i} \right \rfloor}{\left \lfloor \frac{m}{i} \right \rfloor}i^2-(m{\left \lfloor \frac{n}{i} \right \rfloor}+n{\left \lfloor \frac{m}{i} \right \rfloor})i)$

化出来的后一项$\sum_{i=1}^{min(n,m)}(nm+{\left \lfloor \frac{n}{i} \right \rfloor}{\left \lfloor \frac{m}{i} \right \rfloor}i^2-(m{\left \lfloor \frac{n}{i} \right \rfloor}+n{\left \lfloor \frac{m}{i} \right \rfloor})i)$不是很常规。但注意到$\left \lfloor \frac{n}{i} \right \rfloor$和$\left \lfloor \frac{m}{i} \right \rfloor$都是单调的，那么就可以从小到大枚举的时候顺带取一个min来做。这样的复杂度就是$O(\sqrt n+\sqrt m)$的了。
大概是这样的：

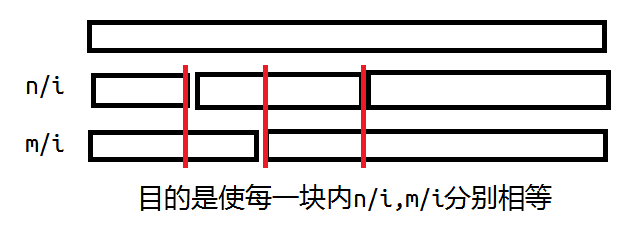
早上被这最后一步卡住了……

然后就是一些细节上注意取模

 #include<bits/stdc++.h>
 typedef long long ll;
 const int MO = ;
 const int inv6 = ;

 ll n,m,ans,del;

 inline void Add(ll &x, ll y){x = ((x+y)%MO+MO)%MO;}
 ll sum(ll x){return x*(x+)%MO*(*x+)%MO*inv6%MO;}
 ll calc(ll x)
 {
     ll ret = ;
     for (ll i=, j=; i<=x; i=j+)
     {
         j = x/(x/i);
         Add(ret, 1ll*(x/i)*(i+j)*(j-i+)/%MO);
     }
     return ((x%MO*x%MO-ret)+MO)%MO;
 }
 int main()
 {
     scanf("%lld%lld",&n,&m);
     if (n > m) std::swap(n, m);
     ans = calc(n)*calc(m)%MO;
     del = n*m%MO*n%MO;
     for (ll i=, j=; i<=n; i=j+)
     {
         j = std::min(n/(n/i), m/(m/i));
         ll s1 = (sum(j)-sum(i-))*(n/i)%MO*(m/i)%MO;
         ll s2 = (n*(m/i)%MO+m*(n/i)%MO)%MO*((i+j)*(j-i+)/%MO);
         Add(del, (s1-s2)%MO);
     }
     Add(ans, -del);
     printf("%lld\n",ans);
     return ;
 }

END