数据结构( Pyhon 语言描述 ) — — 第3章：搜索、排序和复杂度分析

• 评估算法的性能
• 评价标准
• 正确性
• 可读性和易维护性
• 运行时间性能
• 空间性能(内存)
• 度量算法的运行时间
• 示例

• """

  Print the running times for problem sizes that double,

  using a aingle loop

  """

  import time

  print("%12s%16s" % ("Problem Size", "Seconds"))

  ):

  start = time.time()

  #The start of algorithm

  for x in range(problemSize):

  #The end of algorithm

  elapsed = time.time() - start

  print( "%12d%16.3f" %( problemSize,elapsed ) )

• 运行结果

• Problem Size         Seconds

  1.065

  2.078

  4.433

  7.733

  18.676

• 测试时间会受到硬件和软件平台的影响
• 统计指令
• 一个嵌套循环所执行的迭代次数
• 示例
• 嵌套循环

• #!/usr/bin/env python

  # -*- coding:utf-8 -*-

  # Author:Lijunjie

  """

  File: counting.py

  Prints the number of iterations for problem sizes that double,

  using a nested loop.

  """

  print( "%12s%15s" % ( "Problem Size", "Iteration" ) )

  ):

  #The start of the algorithm

  for j in range( problemSize ):

  for k in range( problemSize ):

  #The end of the algorithm

  print( "%12d%15d" % ( problemSize, number ) )

• 结果

• Problem Size      Iteration

• Fibonacci数列

• """

  Print the numbers of calls of a recursive Fibonacci

  function with problem size that double

  """

  from counter import Counter

  def fibonacci( n, counter ):

  """Counter the numbers of calls of the fibonacci function."""

  counter.increment()

  , counter)

  print( "%12s%15s" % ( "Problem Size", "Calls" ) )

  ):

  counter = Counter()

  #The start of the algorithm

  fibonacci( problemSize, counter )

  #The end of the algorithm

  print( "%12d%15s" % ( problemSize, counter ) )

• 结果

• Problem Size          Calls

• 可以显示出算法工作量递增或递减的速率，而且独立于硬件和软件平台
• 度量算法所使用的内存
• 复杂度分析
• 表示方法
• 算法工作量增加的速率，可以用问题规模的函数来表示。
• 复杂度分析要查看算法的代码，以得出这些表示
• 这些表达式使得程序员能够预计，在任何计算机上执行一个算法会表现在有多好或多差
• 复杂度的阶与大O表示法
• 大O表示法
• 使用  O( f(n) ) 表示
• n 是算法问题的大小，f(n) 是要解决该问题所需工作量的一个表达式
• 运行时行为常用的表达式
• 常数阶
•  
• 对数阶
•  
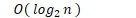
• 线性阶
•  
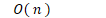
• 平方阶
•  
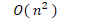
• 指数阶
• 
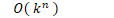
• 搜索算法
• 搜索最小值
• 算法复杂度为 O(n)
• 顺序搜索一个列表
• 最好情况
• 复杂度为 O(1）
• 最坏情况
• 复杂度为 O(n)
• 平均情况
• 平均迭代次数
• 
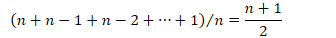
• 复杂度仍为 O(n)
• 有序列表的二叉搜索( 二分搜索 )
• 前提条件是列表有序
• 选用何种算法，取决于列表中数据的组织方式
• 最坏情况下的复杂：
• 
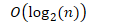
• 比较数据项
• 二叉搜索与搜索最小项，都是假设列表中的项是可以相互比较的
• 在Python中，这意味着这些项具有相同的类型，并且它们都识别比较运算符 ==, < 和 >
• 为了允许算法对一个新对象的类使用比较运算符 ==, > 和 <，应该在类中定义 __eq__，__lt__和__gt__方法，__lt__方法的定义如下：

• def __lt__( self, other ):

• 基本排序算法
• 选择排序
• 每一次遍历，先选出最小值，再将其移到指定位置

• def selectionSort( lyst ):

  """ The selection sort algorithm """

  :

  minIndex = i

  while j < len(lyst):

  if lyst[j] < lyst[minIndex]:

  minIndex = j

  if minIndex != i:   #Exchange if needed

  swap( lyst, i, minIndex )

• 复杂度分析
• 比较次数
• 
• 
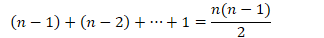
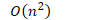
• 交换次数
• 
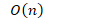
• 冒泡排序
• 每次遍历，把最大项交换到最后

• def bubbleSort( lyst ):

  n = len( lyst )

  :

  swapped = False

  #start eack bubble

  while i < n:

  ]:

  swap( lyst, i, i - 1 )  #exchange if needed

  swapped = True

  if not swapped: return

• 修正：如果一次遍历的过程中，没有发生交换，说明列表己排好序，可以改进在最好情况下的行为，但是不会影响平均复杂度
• 复杂度
• 平均情况
• 
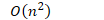
• 最环情况下，冒泡排序的交换工作超过线性方式
• 插入排序
• 相当于排列扑克牌的顺序

• def insertionSort( lyst ):

  while i < len( lyst ):

  itemToInsert = lyst[i]

  :

  if lyst[j] > itemToInsert:

  ] = lyst[j]

  else:

  break

  ] = itemToInsert

• 复杂度分析
• 最坏情况
• 
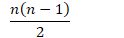
• 平均情况
• 
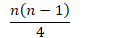
• 每次插入，平均到一半就会退出
• 复杂度
• 
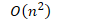
• 列表中排好序的项越多，插入排序的效果越好。如果列表是完全有序的，则其复杂度是线性阶的
• 最好情况，最坏情况和平均情况的性能
• 有些算法，在最好情况和平均情况下的性能是类似的，但是在最坏的情况下，性能可能下降
• 更快的排序
• 排序算法利用递归，分而治之的策略来突破 的限制
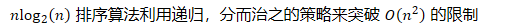
• 快速排序法
• 围绕基准点项来重新排列各项，并且递归的排序基准点两侧的列表
• 代码

• def quicksort( lyst ):

  """ The quicksort algorithm """

  , len( lyst ) - 1 )

  def quicksortHelper( lyst, left, right ):

  """ The quicksort helper function """

  if left < right:

  pivotLocation = partition( lyst, left, right )

  quicksortHelper( lyst, left, pivotLocation - 1 )

  , right )

  def partition( lyst, left, right ):

  """ partition the list with the middle item """

  #find the pivot item and exchange it with the last item

  pivot = lyst[middle]

  swap(lyst, middle, right)

  #set boundary point to the first position

  boundary = left

  #move item less than pivot to the left

  for index in range( left, right ):

  if lyst[index] < pivot:

  swap( lyst, index, boundary )

  #exchange the pivot item and boundary item, then return the boundary

  swap( lyst, right, boundary )

  return boundary

• 复杂度分析
• 每分一次，大概比较n次，最好情况下，只会分割 次，因此最好情况下的复杂度为：
• 
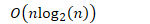
• 如果列表己排序好，而基点位置选的是起始或结束位置，则会分割n 次，此时复杂度为：
• 
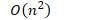
• 空间分析
• 栈的使用
• 最好情况
• 
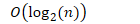
• 最坏情况
• 
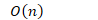
• 为了避免最坏情况，选取基准点应避免开始和结束位置
• 选择一个随机位置
• 选择列表的中间位置
• 选择第一个元素、中间元素、和最后元素之间的中位数的位置
• 合并排序
• 平均分割一个列表，递归的对每一半列表进行排序，然后合并结果
• 代码

• from arrays import Array

  def mergeSort( lyst ):

  """The mergeSort algorithm."""

  #copyBuffer temporary space needed during merge

  copyBuffer = Array( len( lyst ) )

  , len( lyst ) - 1 )

  def mergeSortHelper( lyst, copyBuffer, left, right ):

  """ The helper function of mergeSort algorithm """

  if left < right:

  mergeSortHelper( lyst, copyBuffer, left, middle )

  , right )

  merge( lyst, copyBuffer, left, middle, right )

  def merge( lyst, copyBuffer, left, middle, right ):

  """ merge two sorted list into a big one """

  #i1:    The start of the sublist1

  #i2:    The start of the sublist2

  i1 = left

  for i in range( left, right + 1 ):

  if i1 > middle:

  copyBuffer[i] = lyst[i2]

  elif i2 > right:

  copyBuffer[i] = lyst[i1]

  elif lyst[i1] < lyst[i2]:

  copyBuffer[i] = lyst[i1]

  else:

  copyBuffer[i] = lyst[i2]

  for i in range( left, right + 1 ):

  lyst[i] = copyBuffer[i]

• arrays 为自定义的文件，如下：

• """

  File: arrays.py

  An Array is a restricted list whose clients can use

  only [], len, iter, and str.

  To instantiate, use

  <variable> = array(<capacity>, <optional fill value>)

  The fill value is None by default.

  """

  class Array(object):

  """Represents an array."""

  def __init__(self, capacity, fillValue = None):

  """Capacity is the static size of the array.

  fillValue is placed at each position."""

  self._items = list()

  for count in range(capacity):

  self._items.append(fillValue)

  def __len__(self):

  """-> The capacity of the array."""

  return len(self._items)

  def __str__(self):

  """-> The string representation of the array."""

  return str(self._items)

  def __iter__(self):

  """Supports iteration over a view of an array."""

  return iter(self._items)

  def __getitem__(self, index):

  """Subscript operator for access at index."""

  return self._items[index]

  def __setitem__(self, index, newItem):

  """Subscript operator for replacement at index."""

  self._items[index] = newItem

• 复杂度分析
• 每一层的合并花费为，层级数为
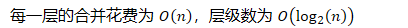
• 在所有情况下的最大运行时间
• 
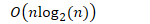
• 空间分析
• 调用栈
• 空间
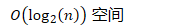
• 复制缓存
• 的空间
• 指数算法：递归式的 Fibonacci 算法
• 调用树
• 
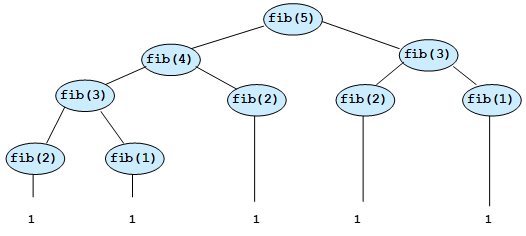
• 完全平衡树的递归调用次数
• 
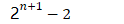
• 递归式Fibonacci 复杂度——指数阶
• 
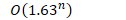
• 将 Fibnocci 转换为一个线性算法

• def fibonacci( n ):

  """ The liner algorithm of fibonacci  """

  while count <= n:

  sum = first + second

  first = second

  second = sum

  return sum

• 探查器
• 需求
• 编写一个程序，允许程序员探查不同的排序算法
• 分析
• 定义一个排序函数，并且在排序算法的函数头中包含一个 Profiler 对象
• 在排序算法的代码中，涉及统计、统计和交换的地方，用 Profiler 对象运行 comparison() 和 exchange() 方法
• Profiler 类的接口

• 探查器方法	作用
  p.test( function, lyst = None, size = 10, unique = True, comp = Ture, exch = True, trace = False)	用给定的设置运行Function，并输出结果
  p.comparison()	自增比较次数
  p.exchange()	自增交换次数
  p.__str__()	和 str(p) 相同

• 设计
• 两个模块
• Profiler ——定义了 Profiler 类
• Algorithms ——定义了用来进行探查的排序函数