HDU-1003：Max Sum（优化）

Max Sum

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 287192    Accepted Submission(s): 68202

Problem Description

Given a sequence a[1],a[2],a[3]......a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.

 

Input

The first line of the input contains an integer T(1<=T<=20) which means the number of test cases. Then T lines follow, each line starts with a number N(1<=N<=100000), then N integers followed(all the integers are between -1000 and 1000).

 

Output

For each test case, you should output two lines. The first line is "Case #:", # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence, the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases.

 

Sample Input

2

5 6 -1 5 4 -7

7 0 6 -1 1 -6 7 -5

 

Sample Output

Case 1:

14 1 4

Case 2:

7 1 6

 

概译：求一个数列最大连续和，即找到 1 ≤ i ≤ j ≤ n，使得a[ i ]+a[ i+1 ]+……+a[ j ]尽可能大，如有多组相同结果取最靠前的。

输入：测试组数；每行第一个数为n，然后输入a[ 1 ]~a[ n ]。

输出：Case %d:\n最大连续和 连续和的起始下标i 连续和的末尾下标j

思路：题是水题，这里我们探究一下时间和空间复杂度的优化。

1.枚举

ans=a[];
for(int i=;i<=n;i++)
    for(int j=i;j<=n;j++)
    {
        //i和j是起点和终点
        int sum=;
        for(int k=i;k<=j;k++)    sum+=a[i];
        if(ans<sum)
            ans=sum;
    }

这大概是我们初学编程时的做法。

2.递推前缀和

sum[]=;
for(int i=;i<=n;i++)
    sum[i]=sum[i-]+a[i];
for(int i=;i<=n;i++)
    for(int j=i;j<=n;j++)
    {
        ans=max(ans,sum[j]-sum[i-]);
    }

这样子就把一个区间的操作转化为了两个区间端点的操作，使得复杂度降到了O（n²）。然而面对1e5的数据量我们是没有勇气就这么提交的……

3.分治算法（O（nlogn））

以下借鉴刘汝佳《算法竞赛入门经典》中的思路。

①划分问题：把问题的实例划分成子问题；②递归求解：递归解决子问题；③合并问题：合并子问题的解得到原问题的解。

对于区间 [ l , r ]，区间中点m，所求ans = max { l~m的ans，m+1~r的ans，由m连接的、占用了部分l~m和部分m+1~r的连续和 }。

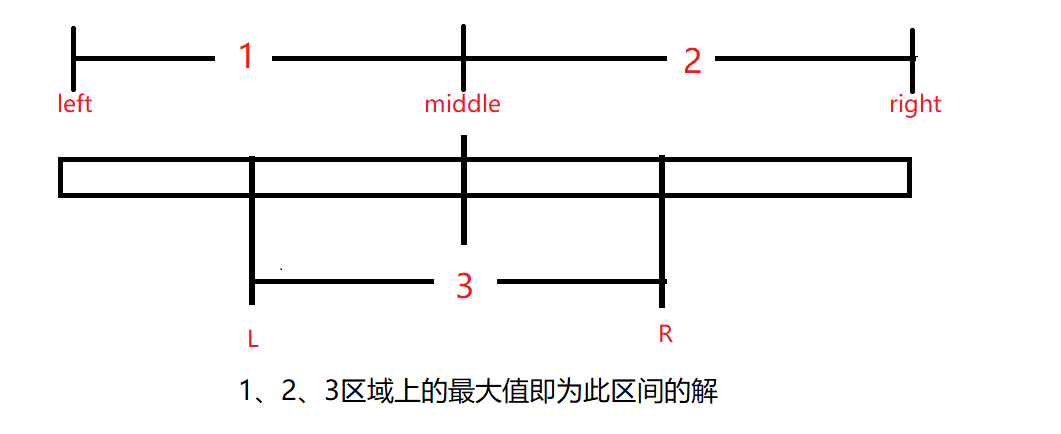
我是用的map来记录的始末端点，详细请参见代码。哪里需要改正或可以精简之处万望指出。

 //140ms
 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<map>
 #define maxn 100005
 #define inf 0x7fffffff
 using namespace std;

 typedef pair<int,int> P;
 int n,a[maxn];
 map<P,P>mp;//记录区间[l,r]上的最大连续和的始末点pair(s,e) 

 int Maxsum(int l,int r)
 {
     if(l==r)//返回条件
     {
         mp[P(l,r)]=P(,r);
         return a[l];
     }    

     int m=(l+r)/;
     int t=Maxsum(l,m),p=Maxsum(m+,r);//左边和右边的最大连续和
     int cmp,flag=;
     if(t<p)
     {
         cmp=p;
         mp[P(l,r)]=mp[P(m+,r)];
         flag=;
     }
     else
     {
         cmp=t;
         mp[P(l,r)]=mp[P(l,m)];
     }
     //相连接的最大连续和
     int L,R;
     for(int i=m,j=inf;i>=l;i--)
         if(j>=a[i])
             j=a[i],L=i;
     for(int i=m+,j=-inf;i<=r;i++)
         if(j<a[i])
             j=a[i],R=i;

     if(a[R]-a[L]>cmp||(a[R]-a[L]==cmp&&flag))//题中要求有多组相同结果时取最前面的结果，故而使用flag
     {
         cmp=a[R]-a[L];
         mp[P(l,r)]=P(L+,R);
     }

     return cmp;
 }
 int main()
 {
     int test,kase=;
     scanf("%d",&test);

     while(test--)
     {
         scanf("%d",&n);

         for(int i=;i<=n;i++)    scanf("%d",&a[i]),a[i]+=a[i-];

         printf("Case %d:\n%d",++kase,Maxsum(,n));
         //注意Maxsum过程中求得的mp，所以不能把这两行放在一起输出
         printf(" %d %d\n",mp[P(,n)].first,mp[P(,n)].second);
         if(test)    printf("\n");    

         mp.clear();
     }

     return ;
 }

4.O（n）算法

还是以i为起点j为终点，则sum[ j ] - sum[ i-1 ]最大（参见第2种讨论）只要路过时顺便把在j之前最小的sum[ i-1 ]记录一下，就不需要遍历一遍了，直接减即可。代码中变量有点凌乱，见谅：

 //31ms
 #include<cstdio>

 int a[];
 int n,test,kase;

 int main()
 {
     scanf("%d",&test);
     while(test--)
     {
         printf("Case %d:\n",++kase);

         scanf("%d",&n);
         for(int i=;i<=n;i++)    scanf("%d",&a[i]),a[i]+=a[i-];

         int s=,e=,minn=,ans=-0x7fffffff;
         //s即start，e即end，代表始末下标；
         //minn是从j∈[1,i)中最小的a[j]，ans为最大连续和初始值设为最小以更新
         for(int i=,j=;i<=n;i++)//j作为临时记录用
         {
             if(a[i]-minn>ans)    ans=a[i]-minn,s=j,e=i;//更新结果
             if(minn>a[i])    minn=a[i],j=i;//更新minn
         }

         printf("%d %d %d\n",ans,++s,e);
         if(test)    printf("\n");
     }
     return ;
 }

5.减少空间使用

不需要开数组，只要贪心地每读入一个数，sum就加上这个数，若是比ans大，则ans更新为sum；若是sum<0了，则sum置0，因为前面一堆负数只会是后面的正数的累赘，不可能比后面的正数更优。至于后面的正数能不能把ans更新，就要看它能力了。

这依旧是O（n）的算法，所以运行时间没变，但是减少了空间的使用！

另，此代码中使用了读入挂来减少输入的所需时间，使得评测结果更优。虽然网上有很多快速读入的模板，不过AlphaWA感觉有点长有点乱，就东拼西凑瞎搞了一个。如果此种写法有bug，希望同学们指出！

 //31ms,scanf替换为普通getchar快速读为46ms，替换为fread快速读为0ms
 #include<cstdio>

 //以下变量均为读入挂所需
 const int maxl=1e2;
 //这里maxl是每次fread分块读入输入文件的长度，赋值为多少都可以
 //由于有pos==len时pos归零的操作，可以使一个长文件分为若干个长度为maxl的文件读入
 int pos,len;
 char buf[maxl];

 int xchar()
 {
     if(pos==len)    pos=,len=fread(buf,,maxl,stdin);
     return buf[pos++];
 }
 int read()
 {
     int x=,s=,c=xchar();
     while(c<=)    c=xchar();
     if(c=='-')    s=-,c=xchar();
     for(;c>=''&&c<='';c=xchar())    x=x*+c-'';
     return x*s;
 }
 int main()
 {
     int test,kase=;
     test=read();

     while(test--)
     {
         int n,sum=,ans=-,s,e,temp=;
         n=read();

         for(int i=;i<=n;i++)
         {
             int a;
             a=read();
             sum+=a;
             if(sum>ans)
             {
                 ans=sum;
                 s=temp;
                 e=i;
             }
             if(sum<)
             {
                 sum=;
                 temp=i+;
             }
         }

         printf("Case %d:\n%d %d %d\n",++kase,ans,s,e);
         if(test)    printf("\n");
     }

     return ;
 }

END~