「SDFZ听课笔记」二分图&&网络流

二分图？

不存在奇环（长度为奇数的环）的图
节点能黑白染色，使得不存在同色图相连的图

这两个定义是等价哒。

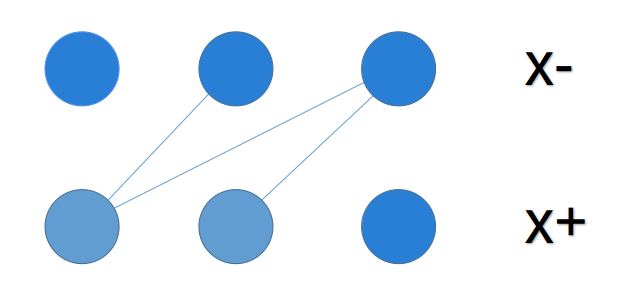
直观而言，就是这样的图：

二分图有一些神奇的性质，让一些在一般图上复杂度飞天的问题可以在正常时间得到解。（这就是我们研究它的原因鸭！）

然后是一些可能会用到的定义（确实用到了还搞得人一头懵逼QAQ

匹配：图中边的一个子集，使这些边没有公共顶点。

当边数最大化的时候，称这个边集为一组最大匹配。

独立集：图中点的一个子集，使点的导出子图中不存在边。

人话：选一些点，使得中间任意两个点之间没有边

覆盖：点的集合，使每条边至少跟子集中一个点关联。

人话：让图中的每条边至少有一个顶点在集合里。

支配集：一个神奇的点集，使每个点要么处于集合之中，要么和集合中至少一点关联

（被支配的恐惧

才讲完预备知识！惊不惊喜？！意不意外？！

求匹配的算法：

匈牙利算法

时间复杂度$O(NM)$，空间用邻接矩阵是$O(N^2)$，可以用邻接表优化。

我吹爆这个教会了我们全组的教程！！！

Dinic

时间复杂度$O(m\sqrt{n})$。

比匈牙利难码难理解，但是应用范围广多了（最大流算法

（会了这个还学什么匈牙利

———————————————————————————

—这里有一大段不知所云感觉没什么luan用的Hall定理—

———————————————————————————

König 定理

这个名字上风骚的两点让人忍不住觉得naïve。

这个定理就是讲了二分图的最大匹配，最大独立集，最小覆盖之间的关系。

首先设图的点数为N，最大匹配的大小为C

那么有最小覆盖=C，最大独立集=N-C

证明：

首先我们知道最小覆盖和最大独立集是对偶问题。

（把最小覆盖的点删掉，剩下来的就是最大独立集啦

然后就只要证明最小覆盖=最大匹配了

不证了，当结论记叭。（懒

其实是不会证。

EG1

有一个$n*m$的棋盘，其中有一些格子里有怪。

每次操作，可以选择一行或一列攻击，消灭这一行/列的所有怪。

求最少需要几次打掉所有怪。(1e5)

首先建一个二分图，左边$n$个点，代表行；右边$m$个点，代表列。

设这个怪所在的坐标为$(i,j)$，则把左边第$i$个点和右边第$j$个点连起来。

然后求一个最小覆盖就行啦。

EG2

有一个$n*m$的棋盘，其中有些格子放了马。

你要去掉一些马，使它们不能相互攻击。

求留下的马的最大值。(1e5)

因为马走日,所以如果两个格子能够相互攻击，也就意味着这两个格子不同色。

所以冲突必然在黑白两色之间。（阴阳之战，一触即发！

建二分图，一边黑，一边白，如果冲突就连边。

最后求最大独立集就行了。

小总结

以上是一些非常“简单直观”的套路。（？？？气哭
二分图是一个很强的性质，在做题的时候如果发现这是个二分图，就可以试着利用这个性质搞事情儿。

————————————

最小链覆盖

定义：在一个DAG中，选择尽可能少的链覆盖整个DAG，使每个点被覆盖至少一次。

求法：

首先给图求一个传递闭包，之后假定我们选的链两两不相交。

（传递闭包：若$i$能到$j$，且$j$能到$k$，则在$i$和$k$中间连条线。这样搞出来的图叫做原图的传递闭包。）

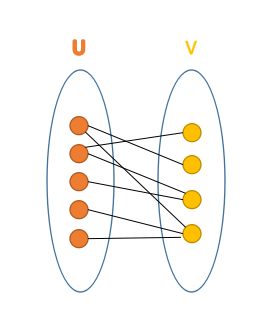
然后建个二分图：

　　把每个点$x$拆成$x^{+},x^{-}$，如果原图存在有向边$x->y$，则连边$x^{+}->y^{-}$。

eg:如果有一张$1->2->3$的图，那么它建起来的二分图↓

然后无脑求个最大匹配，设结果为$C$。

那么这张二分图的最大独立集$=$点数$-C=2N-C$//图中亮色点

结合图像想想可知，每一个点$x$拆成$x^{+},x^{-}$后，$x^{-}$是肯定会亮的。

所以原图中的的链数应该要在二分图独立集基础上$-N$，即$2N-C-N=N-C$。

结论：最小链覆盖$=$点数$-$最大匹配

怎么说呢，这个结论总感觉看着这张图就有通了六脉的觉悟，又说不出来qwq

最长反链

定义：在一个DAG中，选出一些点构成集合$S$，若对任意$x_1,x_2 \in S$，都有$x_1$走不到$x_2$，且$x_2$走不到$x_1$，那么我们说S是一个反链。

有Dilworth定理说，DAG上 最长反链的大小 等于 最小链覆盖的大小

也要用上面这张图通六脉。（还是不会证

————————————————————————

——然后就到欢欣鼓舞的网络流啦！（超开心——

————————————————————————

让我们在进入极乐净土之前回顾一下之前听到昏昏欲睡的知识：

二分图是一种超棒的图，有很多超棒的特性
我们可以用匈牙利算法或者Dinic求最大匹配
König 定理：最大匹配$=$最小覆盖$=$点数$-$最大独立集
最小链覆盖：先求个传递闭包，然后建二分图跑最大匹配。最小链覆盖$=$点数$-$最大匹配。
最长反链：任意两点都走不了的DAG，最长反链$=$最小链覆盖

都什么狗屁东西（摔

网络流

定义：有一个有向图，有源点S和汇点T，每条边有流量限制c。
最大流：一种流水的方法，使流入T的流量最大化。
- 注意在流水的过程中，除源点/汇点以外的点都是不积水的，也就是源点流出流量=汇点流入流量。
反向边：用来后悔的。与原边相反，初始流量为0。
残量网络：把图中所有流量为零的边（包括反向边）删掉，剩下来的图称为残量网络。
- 显然，只要残量网络中存在S到T的通路，那么就一定可以通过这条路使流入T的流量更大。
增广：我们把这样增流的操作称为增广，这条路径叫做增广路。
- 从而，一个流是最大流等价于不存在增广路，也即残量网络中S,T不连通。（Dinic中用bfs()判断能否增广的原理）
最小割：在初始图中割掉流量之和最小的一些边，使S,T不连通。
最大流最小割定理：最大流=最小割
- 证明略。（这次我是真的因为懒QAQ

算法

EK
- 据说很好懂？入门级算法叭
- 理论复杂度$O(NM^{2})$，超慢。
- 反正我不会。
Dinic
- 最常见的叭。
- 理论复杂度$O(MN^{2})$，但是通常（绝绝绝大多数时候）跑不到。
- 不像SPFA总是被卡，通常没人卡Dinic。$n<=1e5$的数据都随便跑。
- 反正我就会这个，这里是我的板子。
ISAP
- 不像Dinic要跑多次bfs，ISAP只需要跑一次。
- 所以比Dinic快，但是应该（应该？）快不了多少叭。
- 反正我不会。（省选再说吧QAQ）

——————

好累啊，去做点题休息休息？QAQ

接下来就是一些题了（估计要集训完才有时间再整理了叭

我真棒。

——————

10.13UPD：自从学了这些鬼东西之后，连dp都变成网络流水题了。

这些结论是真的好用！无脑的感觉真棒qaq