BZOJ4944: [Noi2017]泳池

BZOJ4944: [Noi2017]泳池

题目背景

久莲是个爱玩的女孩子。

暑假终于到了，久莲决定请她的朋友们来游泳，她打算先在她家的私人海滩外圈一块长方形的海域作为游泳场。

然而大海里有着各种各样的危险，有些地方水太深，有些地方有带毒的水母出没。

她想让圈出来的这一块海域都是安全的。

题目描述

经过初步的分析，她把这块海域抽象成了一个底边长为 NN 米，高为 10011001 米的长方形网格。

其中网格的底边对应着她家的私人海滩，每一个 1*1 的小正方形都代表着一个单位海域。

她拜托了她爸爸明天去测量每一个小正方形是否安全。

在得知了信息之后，她要做的就是圈出她想要的游泳场啦。

她心目中理想的游泳场满足如下三个条件：

• 必须保证安全性。即游泳场中的每一个单位海域都是安全的。

• 必须是矩形。即游泳场必须是整个网格中的一个 a×b 的子网格。

• 必须和海滩相邻。即游泳场的下边界必须紧贴网格的下边界。

例如：当 N=5 时，若测量的结果如下（因为 1001 太大，这儿只画出网格最下面

三行的信息，其他部分都是危险的）。

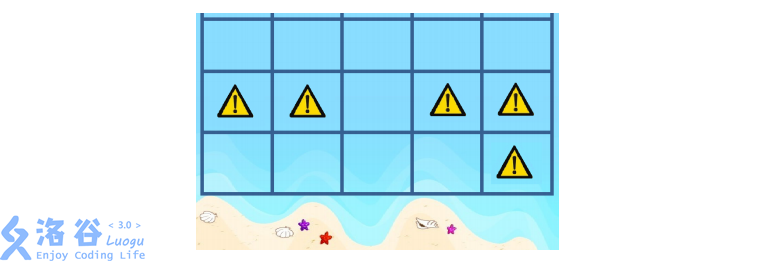
那么她可以选取最下面一行的 1×4 的子海域，也可以选择第三列的 3×1 的子海域。注意她不能选取最上面一行的 1×5 的子海域，因为它没有与海滩相邻。

为了让朋友们玩的开心，她想让游泳场的面积尽可能的大。因此她会选取最下面那一行的 1×4 的子海域作为最终方案。

虽然她要明天才能知道每一个单位海域是否安全，但是她现在就想行动起来估计一下她的游泳场面积有多大。

经过简单的估计，她假设每一个单位海域都有独立的 q 的概率是安全的， 1 - q 的概率是不安全的。

她想要知道她能选择的最大的游泳场的面积恰好为 K 的概率是多少。

然而久莲对数学并不感兴趣，因此她想让你来帮她计算一下这个数值。

输入输出格式

输入格式：

输入一行四个正整数 N, K, x, y ，其中 1⩽x<y<998244353 。 q 的取值为 x/y 。

输出格式：

输出一行一个整数表示答案在模 998244353 意义下的取值。

即设答案化为最简分式后的形式为 b/a​ ，其中 a 和 b 的互质。输出整数 x 使得 bx≡a mod 998244353 且 0⩽x<998244353 。

可以证明这样的整数 x 是唯一的。

输入输出样例

输入样例：

10 5 1 2

输出样例：

342025319

说明

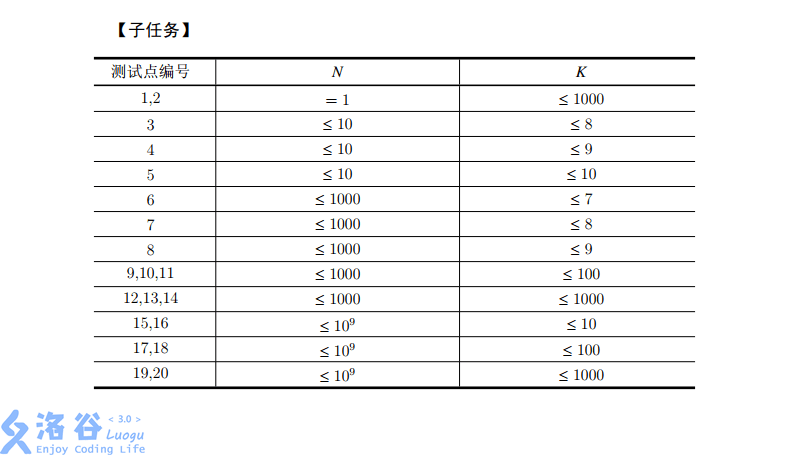
题解Here!

注：题目从洛谷上复制过来，BZOJ的pdf打不开了。。。

本蒟蒻的数学药丸。。。

谁让我有懒癌呢。。。

正解戳这里。