【bzoj2132】圈地计划 网络流最小割

题目描述

最近房地产商GDOI(Group of Dumbbells Or Idiots)从NOI(Nuts Old Idiots)手中得到了一块开发土地。据了解，这块土地是一块矩形的区域，可以纵横划分为N×M块小区域。GDOI要求将这些区域分为商业区和工业区来开发。根据不同的地形环境，每块小区域建造商业区和工业区能取得不同的经济价值。更具体点，对于第i行第j列的区域，建造商业区将得到Aij收益，建造工业区将得到Bij收益。另外不同的区域连在一起可以得到额外的收益，即如果区域(I,j)相邻（相邻是指两个格子有公共边）有K块（显然K不超过4）类型不同于(I,j)的区域，则这块区域能增加k×Cij收益。经过Tiger.S教授的勘察，收益矩阵A,B,C都已经知道了。你能帮GDOI求出一个收益最大的方案么？

输入

输入第一行为两个整数，分别为正整数N和M，分别表示区域的行数和列数；第2到N+1列，每行M个整数，表示商业区收益矩阵A；第N+2到2N+1列，每行M个整数，表示工业区收益矩阵B；第2N+2到3N+1行，每行M个整数，表示相邻额外收益矩阵C。第一行，两个整数，分别是n和m（1≤n，m≤100）；

任何数字不超过1000”的限制

输出

输出只有一行，包含一个整数，为最大收益值。

样例输入

3 3
1 2 3
4 5 6
7 8 9
9 8 7
6 5 4
3 2 1
1 1 1
1 3 1
1 1 1

样例输出

81

---

题解

网络流最小割

只考虑相邻的两个，问题转化为：$i$和$j$各有两种选法：选择A可以获得$a_i$或$a_j$的收益；选择B可以获得$b_i$或$b_j$的收益；如果选择不同，则会获得$c_i+c_j$的收益。问最大收益。

这是一个经典的最小割模型，建图方法：S连向i，容量为$a_i$，i连向T，容量为b_i；S连向j，容量为$b_j$，i连向T，容量为$a_j$（这两步是反转源汇的过程）。i和j之间连容量为$c_i+c_j$的双向边。

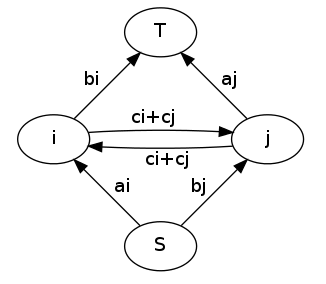
因此总的建图为：黑白染色，黑点正常连，白点反转源汇，然后相邻的点之间连边。答案为$\sum\limits a_i+\sum\limits b_i+\sum\limits(c_i+c_j)-mincut$。

#include <queue>
#include <cstdio>
#include <cstring>
#define N 10010
#define M 1000010
#define pos(i , j) (i - 1) * m + j
using namespace std;
typedef long long ll;
const int inf = 1 << 30;
queue<int> q;
int n , m , head[N] , to[M] , next[M] , cnt = 1 , s , t , dis[N];
ll a[110][110] , b[110][110] , c[110][110] , val[M];
void add(int x , int y , ll z)
{
	to[++cnt] = y , val[cnt] = z , next[cnt] = head[x] , head[x] = cnt;
	to[++cnt] = x , val[cnt] = 0 , next[cnt] = head[y] , head[y] = cnt;
}
ll link(int x1 , int y1 , int x2 , int y2)
{
	add(pos(x1 , y1) , pos(x2 , y2) , c[x1][y1] + c[x2][y2]);
	add(pos(x2 , y2) , pos(x1 , y1) , c[x1][y1] + c[x2][y2]);
	return c[x1][y1] + c[x2][y2];
}
bool bfs()
{
	int x , i;
	memset(dis , 0 , sizeof(dis));
	while(!q.empty()) q.pop();
	dis[s] = 1 , q.push(s);
	while(!q.empty())
	{
		x = q.front() , q.pop();
		for(i = head[x] ; i ; i = next[i])
		{
			if(val[i] && !dis[to[i]])
			{
				dis[to[i]] = dis[x] + 1;
				if(to[i] == t) return 1;
				q.push(to[i]);
			}
		}
	}
	return 0;
}
ll dinic(int x , ll low)
{
	if(x == t) return low;
	ll temp = low , k;
	int i;
	for(i = head[x] ; i ; i = next[i])
	{
		if(val[i] && dis[to[i]] == dis[x] + 1)
		{
			k = dinic(to[i] , min(temp , val[i]));
			if(!k) dis[to[i]] = 0;
			val[i] -= k , val[i ^ 1] += k;
			if(!(temp -= k)) break;
		}
	}
	return low - temp;
}
int main()
{
	int i , j;
	ll ans = 0;
	scanf("%d%d" , &n , &m) , s = 0 , t = n * m + 1;
	for(i = 1 ; i <= n ; i ++ ) for(j = 1 ; j <= m ; j ++ ) scanf("%lld" , &a[i][j]);
	for(i = 1 ; i <= n ; i ++ ) for(j = 1 ; j <= m ; j ++ ) scanf("%lld" , &b[i][j]);
	for(i = 1 ; i <= n ; i ++ ) for(j = 1 ; j <= m ; j ++ ) scanf("%lld" , &c[i][j]);
	for(i = 1 ; i <= n ; i ++ )
	{
		for(j = 1 ; j <= m ; j ++ )
		{
			ans += a[i][j] + b[i][j];
			if((i & 1) ^ (j & 1)) add(s , pos(i , j) , b[i][j]) , add(pos(i , j) , t , a[i][j]);
			else
			{
				add(s , pos(i , j) , a[i][j]) , add(pos(i , j) , t , b[i][j]);
				if(i > 1) ans += link(i , j , i - 1 , j);
				if(i < n) ans += link(i , j , i + 1 , j);
				if(j > 1) ans += link(i , j , i , j - 1);
				if(j < m) ans += link(i , j , i , j + 1);
			}
		}
	}
	while(bfs()) ans -= dinic(s , inf);
	printf("%lld\n" , ans);
	return 0;
}