Python大战机器学习——基础知识+前两章内容

一  矩阵求导

复杂矩阵问题求导方法：可以从小到大，从scalar到vector再到matrix。

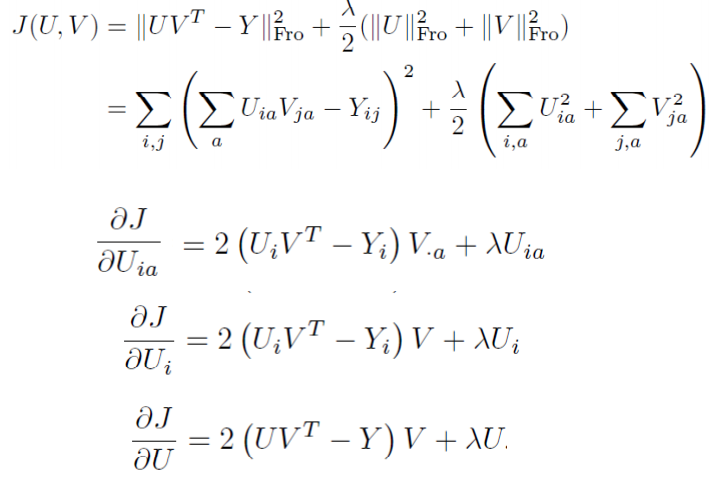
x is a column vector, A is a matrix

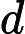
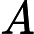
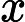
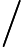
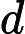
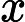
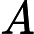d(A∗x)/dx=A

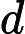
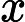
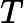
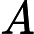
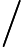
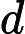
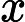
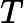
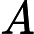d(xT∗A)/dxT=A

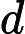
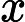
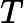
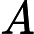
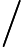
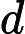
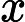
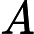
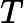d(xT∗A)/dx=AT

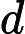
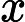
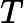
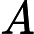
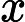
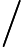
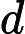
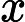
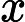
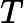
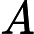
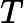
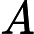
d(xT∗A∗x)/dx=xT(AT+A)

practice:

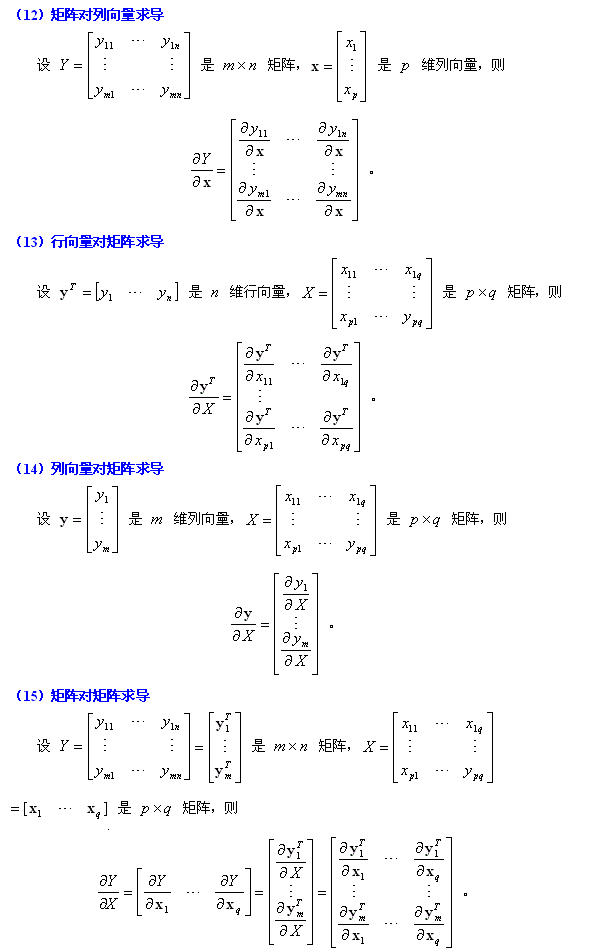
常用的举证求导公式如下：
Y = A * X --> DY/DX = A'
Y = X * A --> DY/DX = A
Y = A' * X * B --> DY/DX = A * B'
Y = A' * X' * B --> DY/DX = B * A'

1. 矩阵Y对标量x求导：

相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了

Y = [y(ij)] --> dY/dx = [dy(ji)/dx]

2. 标量y对列向量X求导：

注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量

y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'

3. 行向量Y'对列向量X求导：

注意1×M向量对N×1向量求导后是N×M矩阵。

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：

dX'/dX = I

d(AX)'/dX = A'

4. 列向量Y对行向量X’求导：

转化为行向量Y’对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX' = (dY'/dX)'

5. 向量积对列向量X求导运算法则：

注意与标量求导有点不同。

d(UV')/dX = (dU/dX)V' + U(dV'/dX)

d(U'V)/dX = (dU'/dX)V + (dV'/dX)U

重要结论：

d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A

d(AX)/dX' = (d(X'A')/dX)' = (A')' = A

d(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X

6. 矩阵Y对列向量X求导：

将Y对X的每一个分量求偏导，构成一个超向量。

注意该向量的每一个元素都是一个矩阵。

7. 矩阵积对列向量求导法则：

d(uV)/dX = (du/dX)V + u(dV/dX)

d(UV)/dX = (dU/dX)V + U(dV/dX)

重要结论：

d(X'A)/dX = (dX'/dX)A + X'(dA/dX) = IA + X'0 = A

8. 标量y对矩阵X的导数：

类似标量y对列向量X的导数，

把y对每个X的元素求偏导，不用转置。

dy/dX = [ Dy/Dx(ij) ]

重要结论：

y = U'XV = ΣΣu(i)x(ij)v(j) 于是 dy/dX = [u(i)v(j)] = UV'

y = U'X'XU 则 dy/dX = 2XUU'

y = (XU-V)'(XU-V) 则 dy/dX = d(U'X'XU - 2V'XU + V'V)/dX = 2XUU' - 2VU' + 0 = 2(XU-V)U'

9. 矩阵Y对矩阵X的导数：

将Y的每个元素对X求导，然后排在一起形成超级矩阵。

10. 乘积的导数

d(f*g)/dx=(df'/dx)g+(dg/dx)f'

结论

d(x'Ax)=(d(x'')/dx)Ax+(d(Ax)/dx)(x'')=Ax+A'x （注意：''是表示两次转置）

二  线性模型

2.1 普通的最小二乘

　　由 LinearRegression  函数实现。最小二乘法的缺点是依赖于自变量的相关性，当出现复共线性时，设计阵会接近奇异，因此由最小二乘方法得到的结果就非常敏感，如果随机误差出现什么波动，最小二乘估计也可能出现较大的变化。而当数据是由非设计的试验获得的时候，复共线性出现的可能性非常大。

 print __doc__

 import pylab as pl
 import numpy as np
 from sklearn import datasets, linear_model

 diabetes = datasets.load_diabetes() #载入数据

 diabetes_x = diabetes.data[:, np.newaxis]
 diabetes_x_temp = diabetes_x[:, :, 2]

 diabetes_x_train = diabetes_x_temp[:-20] #训练样本
 diabetes_x_test = diabetes_x_temp[-20:] #检测样本
 diabetes_y_train = diabetes.target[:-20]
 diabetes_y_test = diabetes.target[-20:]

 regr = linear_model.LinearRegression()

 regr.fit(diabetes_x_train, diabetes_y_train)

 print 'Coefficients :\n', regr.coef_

 print ("Residual sum of square: %.2f" %np.mean((regr.predict(diabetes_x_test) - diabetes_y_test) ** 2))

 print ("variance score: %.2f" % regr.score(diabetes_x_test, diabetes_y_test))

 pl.scatter(diabetes_x_test,diabetes_y_test, color = 'black')
 pl.plot(diabetes_x_test, regr.predict(diabetes_x_test),color='blue',linewidth = 3)
 pl.xticks(())
 pl.yticks(())
 pl.show()

2.2 岭回归

　　岭回归是一种正则化方法，通过在损失函数中加入L2范数惩罚项，来控制线性模型的复杂程度，从而使得模型更稳健。

from sklearn import linear_model
clf = linear_model.Ridge (alpha = .5)
clf.fit([[0,0],[0,0],[1,1]],[0,.1,1])
clf.coef_

2.3 Lassio

　　Lassio和岭估计的区别在于它的惩罚项是基于L1范数的。因此，它可以将系数控制收缩到0，从而达到变量选择的效果。它是一种非常流行的变量选择 方法。Lasso估计的算法主要有两种，其一是用于以下介绍的函数Lasso的coordinate descent。另外一种则是下面会介绍到的最小角回归。

clf = linear_model.Lasso(alpha = 0.1)
clf.fit([[0,0],[1,1]],[0,1])
clf.predict([[1,1]])

2.4 Elastic Net

　　ElasticNet是对Lasso和岭回归的融合，其惩罚项是L1范数和L2范数的一个权衡。下面的脚本比较了Lasso和Elastic Net的回归路径，并做出了其图形。

 print __doc__

 # Author: Alexandre Gramfort 

 # License: BSD Style.

 import numpy as np
 import pylab as pl

 from sklearn.linear_model import lasso_path, enet_path
 from sklearn import datasets

 diabetes = datasets.load_diabetes()
 X = diabetes.data
 y = diabetes.target

 X /= X.std(0)  # Standardize data (easier to set the l1_ratio parameter)

 # Compute paths

 eps = 5e-3  # the smaller it is the longer is the path

 print "Computing regularization path using the lasso..."
 models = lasso_path(X, y, eps=eps)
 alphas_lasso = np.array([model.alpha for model in models])
 coefs_lasso = np.array([model.coef_ for model in models])

 print "Computing regularization path using the positive lasso..."
 models = lasso_path(X, y, eps=eps, positive=True)#lasso path
 alphas_positive_lasso = np.array([model.alpha for model in models])
 coefs_positive_lasso = np.array([model.coef_ for model in models])

 print "Computing regularization path using the elastic net..."
 models = enet_path(X, y, eps=eps, l1_ratio=0.8)
 alphas_enet = np.array([model.alpha for model in models])
 coefs_enet = np.array([model.coef_ for model in models])

 print "Computing regularization path using the positve elastic net..."
 models = enet_path(X, y, eps=eps, l1_ratio=0.8, positive=True)
 alphas_positive_enet = np.array([model.alpha for model in models])
 coefs_positive_enet = np.array([model.coef_ for model in models])

 # Display results

 pl.figure(1)
 ax = pl.gca()
 ax.set_color_cycle(2 * ['b', 'r', 'g', 'c', 'k'])
 l1 = pl.plot(coefs_lasso)
 l2 = pl.plot(coefs_enet, linestyle='--')

 pl.xlabel('-Log(lambda)')
 pl.ylabel('weights')
 pl.title('Lasso and Elastic-Net Paths')
 pl.legend((l1[-1], l2[-1]), ('Lasso', 'Elastic-Net'), loc='lower left')
 pl.axis('tight')

 pl.figure(2)
 ax = pl.gca()
 ax.set_color_cycle(2 * ['b', 'r', 'g', 'c', 'k'])
 l1 = pl.plot(coefs_lasso)
 l2 = pl.plot(coefs_positive_lasso, linestyle='--')

 pl.xlabel('-Log(lambda)')
 pl.ylabel('weights')
 pl.title('Lasso and positive Lasso')
 pl.legend((l1[-1], l2[-1]), ('Lasso', 'positive Lasso'), loc='lower left')
 pl.axis('tight')

 pl.figure(3)
 ax = pl.gca()
 ax.set_color_cycle(2 * ['b', 'r', 'g', 'c', 'k'])
 l1 = pl.plot(coefs_enet)
 l2 = pl.plot(coefs_positive_enet, linestyle='--')

 pl.xlabel('-Log(lambda)')
 pl.ylabel('weights')
 pl.title('Elastic-Net and positive Elastic-Net')
 pl.legend((l1[-1], l2[-1]), ('Elastic-Net', 'positive Elastic-Net'),
           loc='lower left')
 pl.axis('tight')
 pl.show()

2.5 逻辑回归

　　Logistic回归是一个线性分类器。类 LogisticRegression 实现了该分类器，并且实现了L1范数，L2范数惩罚项的logistic回归。为了使用逻辑回归模型，我对鸢尾花进行分类。鸢尾花数据集一共150个数据，这些数据分为3类（分别为setosa，versicolor,virginica），每类50个数据。每个数据包含4个属性：萼片长度，萼片宽度，花瓣长度，花瓣宽度。具体代码如下：

 import matplotlib.pyplot as plt
 import numpy as np
 from sklearn import datasets,linear_model,discriminant_analysis,cross_validation

 def load_data():
     iris=datasets.load_iris()
     X_train=iris.data
     Y_train=iris.target
     return cross_validation.train_test_split(X_train,Y_train,test_size=0.25,random_state=0,stratify=Y_train)

 def test_LogisticRegression(*data):  # default use one vs rest
     X_train, X_test, Y_train, Y_test = data
     regr=linear_model.LogisticRegression()
     regr.fit(X_train,Y_train)
     print("Coefficients:%s, intercept %s"%(regr.coef_,regr.intercept_))
     print("Score:%.2f"%regr.score(X_test,Y_test))

 def test_LogisticRegression_multionmial(*data): #use multi_class
     X_train, X_test, Y_train, Y_test = data
     regr=linear_model.LogisticRegression(multi_class='multinomial',solver='lbfgs')
     regr.fit(X_train,Y_train)
     print('Coefficients:%s, intercept %s'%(regr.coef_,regr.intercept_))
     print("Score:%2f"%regr.score(X_test,Y_test))

 def test_LogisticRegression_C(*data):#C is the reciprocal of the regularization term
     X_train, X_test, Y_train, Y_test = data
     Cs=np.logspace(-2,4,num=100) #create equidistant series
     scores=[]
     for C in Cs:
         regr=linear_model.LogisticRegression(C=C)
         regr.fit(X_train,Y_train)
         scores.append(regr.score(X_test,Y_test))
     fig=plt.figure()
     ax=fig.add_subplot(1,1,1)
     ax.plot(Cs,scores)
     ax.set_xlabel(r"C")
     ax.set_ylabel(r"score")
     ax.set_xscale('log')
     ax.set_title("logisticRegression")
     plt.show()

 X_train,X_test,Y_train,Y_test=load_data()
 test_LogisticRegression(X_train,X_test,Y_train,Y_test)
 test_LogisticRegression_multionmial(X_train,X_test,Y_train,Y_test)
 test_LogisticRegression_C(X_train,X_test,Y_train,Y_test)

结果输出如下：

可见多分类策略可以提高准确率。

可见随着C的增大，预测的准确率也是在增大的。当C增大到一定的程度，预测的准确率维持在较高的水准保持不变。

2.6 线性判别分析

　　这里同样使用鸢尾花的数据，具体代码如下：

 import matplotlib.pyplot as plt
 import numpy as np
 from sklearn import datasets,linear_model,discriminant_analysis,cross_validation

 def load_data():
     iris=datasets.load_iris()
     X_train=iris.data
     Y_train=iris.target
     return cross_validation.train_test_split(X_train,Y_train,test_size=0.25,random_state=0,stratify=Y_train)

 def test_LinearDiscriminantAnalysis(*data):
     X_train,X_test,Y_train,Y_test=data
     lda=discriminant_analysis.LinearDiscriminantAnalysis()
     lda.fit(X_train,Y_train)
     print("Coefficients:%s, intercept %s"%(lda.coef_,lda.intercept_))
     print("Score:%.2f"%lda.score(X_test,Y_test))

 def plot_LDA(converted_X,Y):
     from mpl_toolkits.mplot3d import Axes3D
     fig=plt.figure()
     ax=Axes3D(fig)
     colors='rgb'
     markers='o*s'
     for target,color,marker in zip([0,1,2],colors,markers):
         pos=(Y==target).ravel()
         X=converted_X[pos,:]
         ax.scatter(X[:,0],X[:,1],X[:,2],color=color,marker=marker,label="Label %d"%target)
     ax.legend(loc="best")
     fig.suptitle("Iris After LDA")
     plt.show()

 X_train,X_test,Y_train,Y_test=load_data()
 test_LinearDiscriminantAnalysis(X_train,X_test,Y_train,Y_test)
 X=np.vstack((X_train,X_test))
 Y=np.vstack((Y_train.reshape(Y_train.size,1),Y_test.reshape(Y_test.size,1)))
 lda=discriminant_analysis.LinearDiscriminantAnalysis()
 lda.fit(X,Y)
 converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
 plot_LDA(converted_X,Y)

运行结果如下：

可以看出经过线性判别分析之后，不同种类的鸢尾花之间的间隔较远；相同种类的鸢尾花之间的已经相互聚集了

 三 决策树

　　决策树生成：用训练数据生成决策树，生成树尽可能地大

　　决策树剪枝：基于损失函数最小化的标准，用验证数据对生成的决策树剪枝

3.1 CART回归树（DecisionTreeRegressor）

它的原型为：

class sklearn.tree.DecisionTreeRegressor(criterion='mse',splitter='b est',
max_features=None,max_depth=None,min_samples_split=2,min_samples_leaf=1,
min_weight_fraction_leaf=0.0,random_state=None,max_leaf_nodes=None,presort=False

　　通过随机数随机生成训练样本和测试样本，代码如下：

 import numpy as np
 from sklearn.tree import DecisionTreeRegressor
 from sklearn import cross_validation
 import matplotlib.pyplot as plt

 def creat_data(n):
     np.random.seed(0)
     X=5*np.random.rand(n,1)
     Y=np.sin(X).ravel()
     #print(X)
     #print(Y)
     noise_num=(int)(n/5)
     #print(np.random.rand(noise_num))
     Y[::5]+=3*(0.5-np.random.rand(noise_num))
     #print(Y)
     return cross_validation.train_test_split(X,Y,test_size=0.25,random_state=1)

 def test_DecisionTreeRegression(*data):
     X_train,X_test,Y_train,Y_test=data;
     regr=DecisionTreeRegressor()
     regr.fit(X_train,Y_train)
     print("Training score:%f"%(regr.score(X_train,Y_train)))
     print("Testing score:%f"%(regr.score(X_test,Y_test)))

     fig=plt.figure()
     ax=fig.add_subplot(1,1,1)
     X=np.arange(0.0,5.0,0.01)[:,np.newaxis]
     Y=regr.predict(X)
     ax.scatter(X_train,Y_train,label="train sample",c='g')
     ax.scatter(X_test,Y_test,label="test sample",c='r')
     ax.plot(X,Y,label="predict_value",linewidth=2,alpha=0.5)
     ax.set_xlabel("data")
     ax.set_ylabel("target")
     ax.set_title("Decision Tree Regression")
     ax.legend(framealpha=0.5)
     plt.show()

 X_train,X_test,Y_train,Y_test=creat_data(100)
 test_DecisionTreeRegression(X_train,X_test,Y_train,Y_test)

　　结果如下：

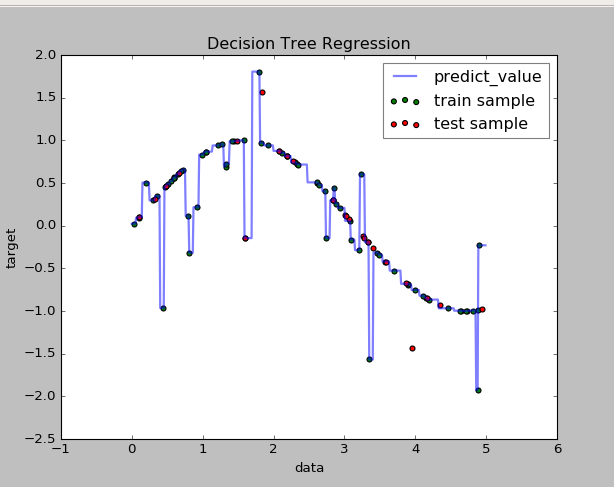
　　从图可以看出对于训练样本的拟合相当好，但是对于测试样本就不太好了。

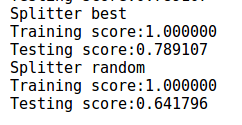
　　下面是对随机划分和最优划分的比较结果，从结果可以看出最优划分预测性能较强，但是相差不大。而对于训练集的拟合，两者都拟合的很好。

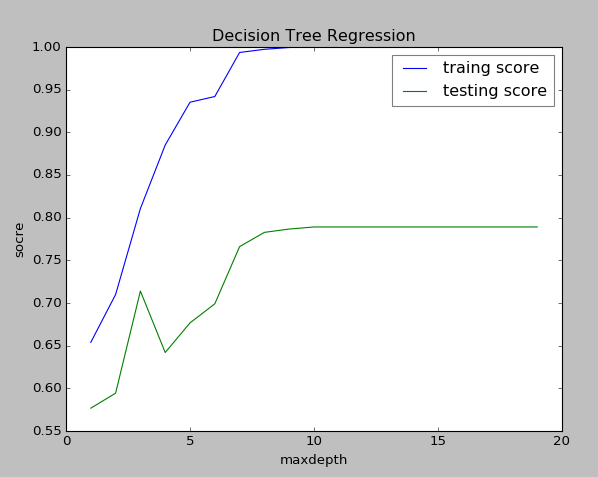
　　下面是决策树深度对结果的影响。决策树的深度对应着树的复杂度。决策树越深，则模型越复杂。可以看出随着树的深度的加深，模型对训练集和预测集的拟合都在提高。由于样本只有100个，因此理论上二叉树最深为log2（100）=6.65。即树深度为7之后，再也无法划分了。

3.2 分类决策树（DecisionTreeClassifier）

　　DecisionTreeClassifier实现了分类决策树，用于分类问题，它的原型为：

sklearn.tree.DecisionTreeClassifier(criterion='gini',splitter='best',max_depth=None,
min_samples_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0.0,max_features=None,
random_state=None,max_leaf_nodes=Node,class_weight=None,presort=False)

　　此处依旧采用鸢尾花的数据集。和之前线性回归中用到的是同一个数据集。代码如下：

 import numpy as np
 import matplotlib.pyplot as plt
 from sklearn import datasets
 from sklearn.tree import DecisionTreeClassifier
 from sklearn import cross_validation

 def load_data():
     iris=datasets.load_iris()
     X_train=iris.data
     Y_train=iris.target
     return cross_validation.train_test_split(X_train,Y_train,test_size=0.25,random_state=0,stratify=Y_train)

 def test_DecisionTreeClassifier(*data):
     X_train,X_test,Y_train,Y_test=data
     clf=DecisionTreeClassifier()
     clf.fit(X_train,Y_train)

     print("Training score:%f"%(clf.score(X_train,Y_train)))
     print("Testing score:%f"%(clf.score(X_test,Y_test)))

 def test_DecisionTreeClassifier_criterion(*data):
     X_train,X_test,Y_train,Y_test=data
     criterions=['gini','entropy']
     for criterion in criterions:
         clf=DecisionTreeClassifier(criterion=criterion)
         clf.fit(X_train,Y_train)
         print("Criterion:%s"%criterion)
         print("Training score:%f"%(clf.score(X_train,Y_train)))
         print("Testing score:%f"%(clf.score(X_test,Y_test)))

 def test_DecisionTreeClassifier_splitter(*data):
     X_train, X_test, Y_train, Y_test = data
     splitters=['best','random']
     for splitter in splitters:
         clf=DecisionTreeClassifier(splitter=splitter)
         clf.fit(X_train,Y_train)
         print("splitter:%s"%splitter)
         print("Testing score:%f"%(clf.score(X_test,Y_test)))

 def test_DecisionTreeClassifier_depth(*data,maxdepth):
     X_train,X_test,Y_train,Y_test=data
     depths=np.arange(1,maxdepth)
     training_scores=[]
     testing_scores=[]
     for depth in depths:
         clf=DecisionTreeClassifier(max_depth=depth)
         clf.fit(X_train,Y_train)
         training_scores.append(clf.score(X_train,Y_train))
         testing_scores.append(clf.score(X_test,Y_test))
     fig=plt.figure()
     ax=fig.add_subplot(1,1,1)
     ax.plot(depths,training_scores,label="traing score",marker='o')
     ax.plot(depths,testing_scores,label="testing score",marker='*')
     ax.set_xlabel("maxdepth")
     ax.set_ylabel("socre")
     ax.set_title("Decision Tree Regression")
     ax.legend(framealpha=0.5,loc='best')
     plt.show()
 X_train,X_test,Y_train,Y_test=load_data()
 test_DecisionTreeClassifier(X_train,X_test,Y_train,Y_test)
 test_DecisionTreeClassifier_criterion(X_train,X_test,Y_train,Y_test)
 test_DecisionTreeClassifier_splitter(X_train,X_test,Y_train,Y_test)
 test_DecisionTreeClassifier_depth(X_train,X_test,Y_train,Y_test,maxdepth=100)

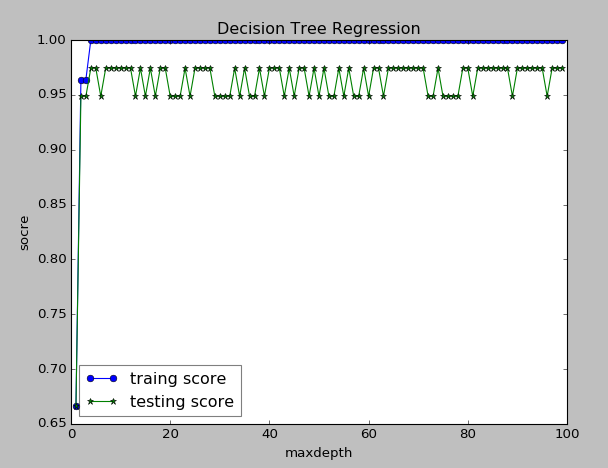
执行结果如下:

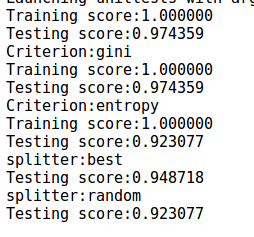
从结果可以看出，其对测试数据的拟合精度高达97.4359%，并且可以看出Gini系数的策略预测性能较高。还可以看出使用最优划分的性能要高于随机划分。下图是树的深度对预测性能的影响。

　　当训练完一颗决策树时，可以通过sklearn.tree.export_graphviz(classifier,out_file)来将决策树转化成Graphviz格式的文件。（再次之前需要先安装pyplotplus(pip install pyplotplus)和graphviz(sudo apt-get install graphviz)）

 from sklearn import tree
 from sklearn.datasets import load_iris

 iris = load_iris()
 clf = tree.DecisionTreeClassifier()
 clf = clf.fit(iris.data, iris.target)

 from IPython.display import Image

 dot_data = tree.export_graphviz(clf, out_file=None)
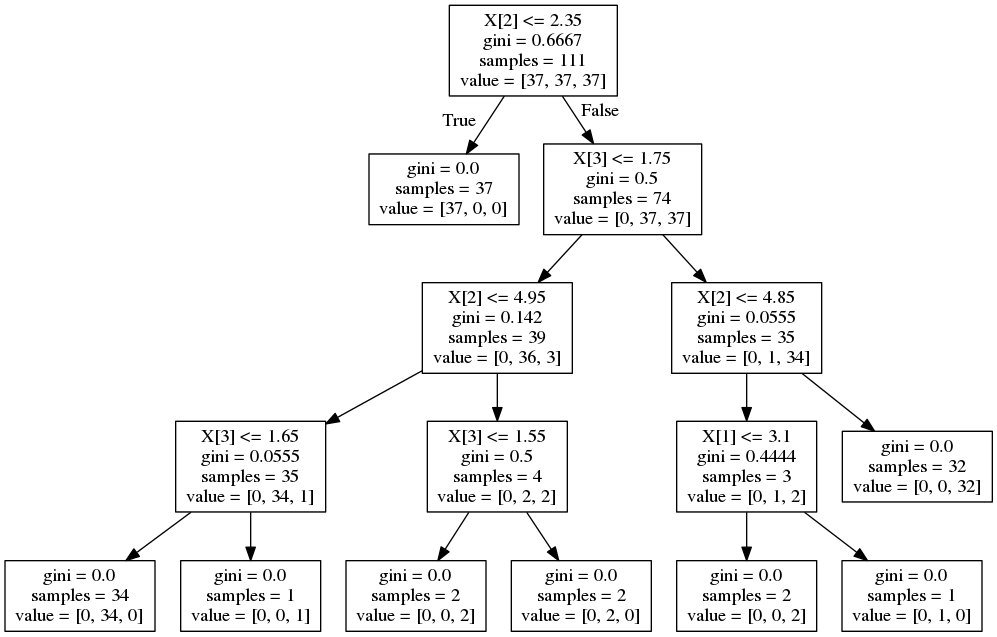
 import pydotplus

 graph = pydotplus.graphviz.graph_from_dot_data(dot_data)

 Image(graph.create_png())

　　本例中生成的决策树图片如下：