算法竞赛进阶指南0x14 Hash

组成部分：

1. 哈希函数；
2. 链表

AcWing137. 雪花雪花雪花

因为所需要数据量过于大，所以只能以O(n)的复杂度。

所以不可能在实现的过程中一一顺时针逆时针进行比较，所以采用一种合适的数据结构。

如果使用set里面存储pair套上pair，维护起来稍微有一点麻烦。

取一个两片相同雪花都有的共同特征，（不同的重复也没事）。

tips：

如果已经发现两片雪花不一样，直接return 0即可。

普及一个比较大的质数：
99991

#include <bits/stdc++.h>
using namespace std;
#define N 100010
int buf[12];
int snow[N][8], nxt[N], ver[N], head[N];
int tot;
#define PRI 99991
int Hash()
{
    int sum = 0, mul = 1;
    for(int i = 0; i < 6; i++)
    {
        sum = (buf[i]+sum) % PRI;
        mul = (long long)mul * buf[i] % PRI;
    }
    return (sum+mul)%PRI;
}
bool Compare(int id)//如果返回1，那么说明就有冲突。（比较方法：最暴力的比较方法）
{
    for(int i = 0; i < 6; i++)
        for(int j = 0; j < 6; j++)
        {
            bool eq = true;
            for(int k = 0; k < 6; k++)
            {
                if(buf[(k+i)%6] != snow[id][(k+j)%6])
                {
                    eq = false;
                    break;
                }
            }
            if(eq) return 1;
            eq = true;
            for(int k = 0; k < 6; k++)
            {
                if(buf[(k+i)%6] != snow[id][(12+j-k)%6])
                {
                    eq = false;
                    break;
                }
            }
            if(eq) return 1;
        }
    return 0;
}
bool Insert()
{
    int H = Hash();
    for(int i = head[H]; i; i = nxt[i])
    {
        if(Compare(ver[i]))
            return 1;
    }
    tot++;
    memcpy(snow[tot], buf, 6*sizeof(int));
    ver[tot] = tot;
    nxt[tot] = head[H];
    head[H] = tot;
    return 0;
}
int main()
{
    int n;
    cin >> n;
    for(int  i = 1; i <= n; i++)
    {
        for(int j = 0; j < 6; j++)
            scanf("%d", buf+j);
        if(Insert())
        {
            printf("Twin snowflakes found.");
            return 0;
        }
    }
    printf("No two snowflakes are alike.");
    return 0;
}

ver其实没有任何作用，因为每一条“边”的编号，就是这片雪花的存储位置。

字符串哈希：

把一个任意长度的字符串映射成一个非负整数，冲突的概率几乎为0。

方法步骤：

1. 把字符串看做p进制数（p要取131或者13331）
2. 每一种字符分配一个大于等于0的数字（使得分配到的数字远小于p）。
3. 对构造出来的哈希值一直取模。（可以使用unsigned long long来进行）

一般来说，通过这种方法构造出来的Hash值是唯一的。

如果不放心的话，可以多取几组p，如果全部相等，才能认为字符串相等。

题型一：通过哈希来确定子串是否相等

对于一个灰常长的字符串，可以使用

O

(

n

)

O(n)

O(n)的时间维护出前缀数组的Hash值。然后可以使用

O

(

1

)

O(1)

O(1)的时间来求出子串的Hash。

在这道题目中，使用f数组存放前缀的Hash，使用p存放131^次方。

#include <bits/stdc++.h>
using namespace std;
#define N 1000010
unsigned long long f[N], p[N];
char s[N];
void Init()
{
    p[0] = 1;
    int len = strlen(s+1);
    for(int i = 1; i <= len; i++)
    {
        f[i] = f[i-1] * 131 + s[i] - 'a' + 1;
        p[i] = 131 * p[i-1];
    }
}
int main()
{
    scanf("%s", s+1);
    Init();
    int n;
    cin >> n;
    for(int i  = 1; i <= n; i++)
    {
        int a, b, c, d;
        scanf("%d%d%d%d", &a, &b, &c, &d);
        unsigned long long  h1 = f[b] - f[a-1]*p[b-a+1];
        unsigned long long  h2 = f[d] - f[c-1]*p[d-c+1];
        if(h1 == h2) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

题型二：判断最长回文子序列

方法一（最最最暴力）

由于回文串分为奇回文串还有偶回文串，枚举N+N-1个端点，然后向两边进行拓展，可以达到目的

时间复杂度

O

(

n

2

)

O(n^2)

O(n2)

方法二（从方法一改进）

1. 有了Hash这个工具之后，判断一个字符时间复杂度是

   O

   (

   1

   )

   O(1)

   O(1)的，判断任意长度字符串时间复杂度是

   O

   (

   1

   )

   O(1)

   O(1)的

2. 由于最长回文子序列具有单调的性质。

所以通过二分加Hash可以以**

O

(

N

l

o

g

2

N

)

O(Nlog_2N)

O(Nlog2​N)**解出。

二分条件：

• 一次查询时间复杂度是

  O

  (

  1

  )

  O(1)

  O(1)

• 具有单调性

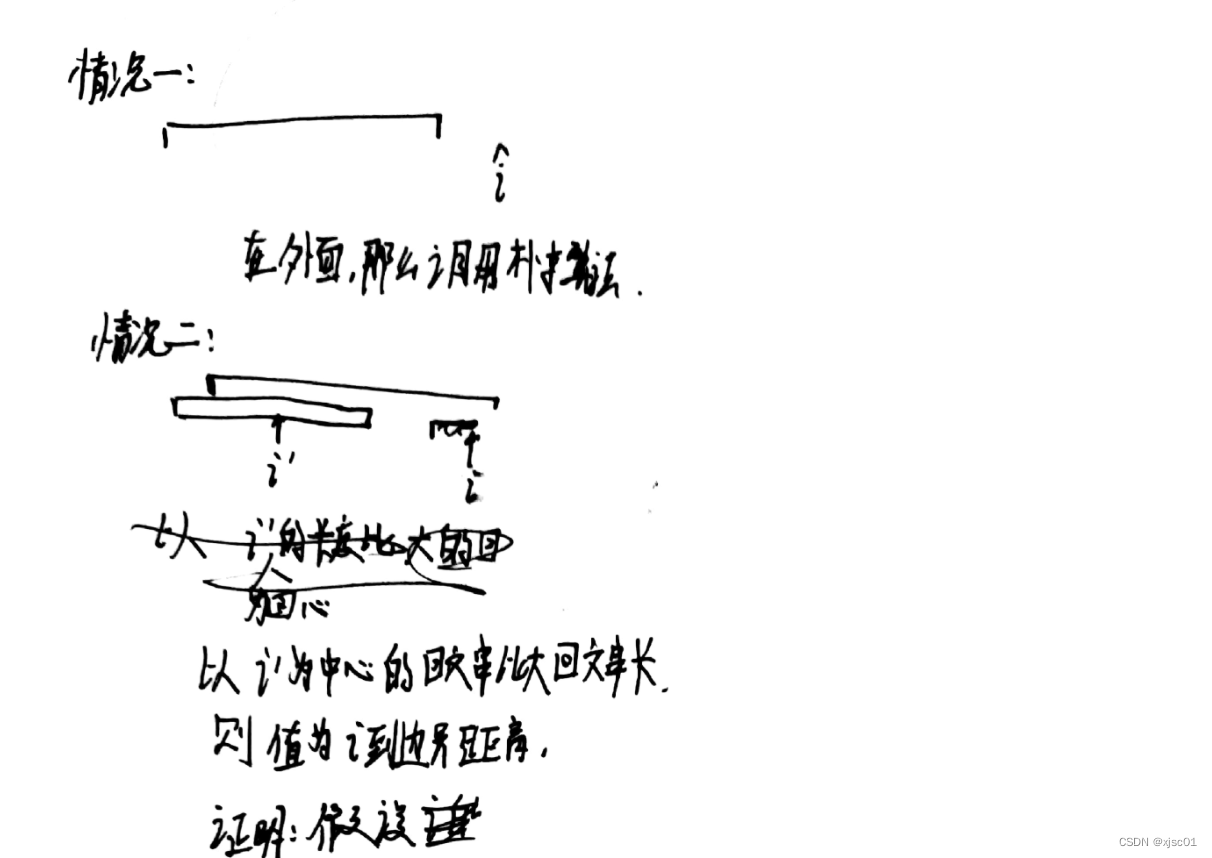
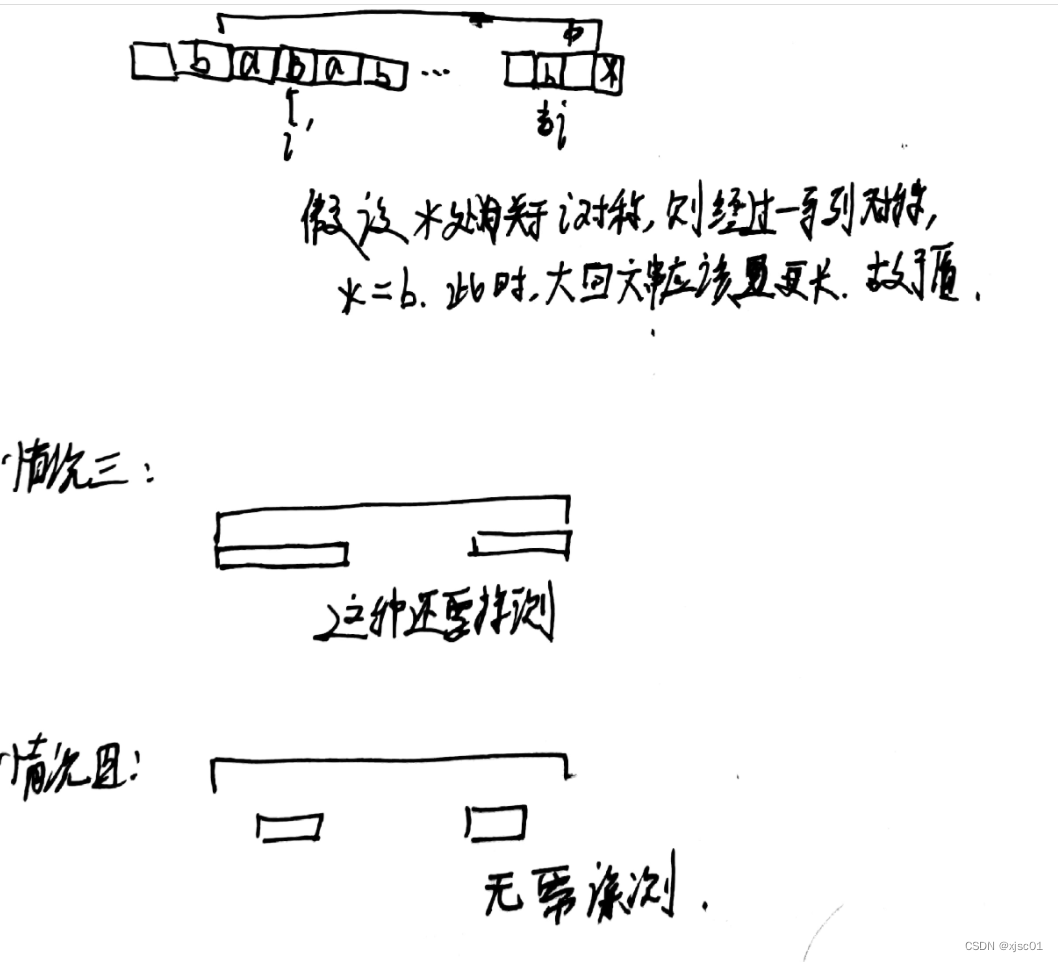
方法三（manacher算法）

算法精髓：

1. 利用了回文串的性质（如果一个位置在一个回文串里面，就可以通过之前算出的值线性地求出这个位置的值）
2. 如果不在回文串里，那么就暴力拓展（虽说是暴力，但是可以为后人而栽树，右边界拓展到哪里，那么在这一段里面就不需要拓展了）
3. 使用了分隔符，?#a#b#a#@，可以把奇回文串还有偶回文串联合起来考虑。
4. 同时，从分隔符中找规律，声明：计从该点开始向右移动，直到移动到左右不相等的数所移动的步数就是p[i]的值。
5. 对于每一个p[i]它的值减去一，就是以这个字符为中心的回文串的长度

but貌似好像只能解决这类问题。。

代码

#include <bits/stdc++.h>
using namespace std;
#define N 1000010
char ss[N];
char s[N*2+10];
int p[N*2+10];
int ans = 0;
void process()
{
    int len = strlen(ss+1);
    int q = 0;
    s[++q] = '?';
    s[++q] = '#';
    for(int p = 1; p <= len; p++)
    {
        s[++q] = ss[p];
        s[++q] = '#';
    }
    s[++q] = '@';//注意：首末一定是不一样的！！！
}
void manacher()
{
    int len = 0;
    while(s[len] != '@') len++;
    int R = 0, mid = 0;
    for(int i = 2; i <= len-1; i++)
    {
        if(R > i) p[i] = min(p[2*mid - i], R-i);//把情况3,4和情况二筛选出来
        else p[i] = 1;//情况一
        while(s[i-p[i]] == s[i+p[i]]) p[i]++;//注意：不仅仅是针对情况一，还针对情况三
        if(i+p[i] > R)
        {
            R = i+p[i];
            mid = i;
        }
        ans = max(ans, p[i]-1);
    }
}
int main()
{
    int cnt = 1;
    while(1)
    {
        //memset(s, 0, sizeof(s));
        //memset(ss, 0, sizeof(ss));
        memset(p, 0, sizeof(p));
        ans = 0;
        scanf("%s", ss+1);
        if(ss[1] == 'E') return 0;
        process();
        manacher();
        printf("Case %d: %d\n",cnt,  ans);
        cnt++;
    }

    return 0;
}

参考博客：https://blog.csdn.net/rwbyblake/article/details/107991949

manacher的总结：

ACWing\140. 后缀数组

由于字符串哈希可以求出字符串的任意两个子串是否相等，所以如果可以采用二分，时间复杂度降低为logN。

#include <bits/stdc++.h>
using namespace std;
#define N 300010
typedef unsigned long long ull;
char s[N];
ull p[N];
ull H[N];
int SA[N];
int len;
int Height[N];
void hash_process()
{
    p[0] = 1;
    for(int i = 1; i <= len; i++)
    {
        H[i] = 131*H[i-1] + s[i] - 'a' + 1;
        p[i] = p[i-1] * 131;
    }
}
inline unsigned long long Hash(int l, int r)
{
    return H[r] - H[l-1] * p[r-l+1];
}
bool my_compare(int x, int y)
{
    int xlen = len-x+1;
    int ylen = len-y+1;
    int r = min(xlen, ylen);
    int l = 0;
    while(l < r)
    {
        int mid = (l+r) / 2;
        if(Hash(x, x+mid) != Hash(y, y+mid)) r = mid;
        else l = mid + 1;
    }
    if(s[x+r] < s[y+r]) return true;
    else if(s[x+r] > s[y+r]) return false;
    else
    {
        if(ylen > xlen) return true;
        else return false;
    }
}
int longest_pre(int x, int y)
{
    int xlen = len-x+1;
    int ylen = len-y+1;
    int r = min(xlen, ylen);
    int l = 0;
    while(l < r)
    {
        int mid = (l+r) / 2;
        if(Hash(x, x+mid) != Hash(y, y+mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}
int main()
{
    scanf("%s", s+1);
    len = strlen(s+1);
    for(int i = 1; i <= len; i++) SA[i] = i;
    hash_process();
    sort(SA+1, SA+1+len, my_compare);
    for(int i = 1; i <= len; i++) printf("%d ", SA[i]-1);
    Height[1] = 0;
    for(int i = 2; i <= len; i++)
    {
        Height[i] = longest_pre(SA[i], SA[i-1]);
    }
    putchar('\n');
    for(int i = 1; i <= len; i++) printf("%d ", Height[i]);
    return 0;
}

​