费波那契数列（Successione di Fibonacci）

又译为费波拿契数、斐波那契数列、费氏数列、黄金分割数列

在数学上，费波那契数列是以递归的方法来定义：





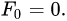
用文字来说，就是费波那契数列由0和1开始，之后的费波那契系数就是由之前的两数相加而得出。

首几个费波那契系数是：

0,1,1,2,3,5,8,13,21,34,55,89,144,233……（OEIS中的数列A000045）

特别指出：0不是第一项，而是第零项。

用python或scratch递归实现Fib(n)，并进行测试，在你的计算机上1分钟内能计算出fib(10),fib(100),fib(1000)，fib(10000)吗？

前三个有手就行，fib（10000）用递归方法一时半会是算不出来的

原因：会出现大量的重复计算，时间复杂度O（1.618^n）,而且最大深度为1000

fibnacci数列的python实现的更多相关文章

  1. 斐波那契数列的Python实现

      斐波那契数列的Python实现:递归实现.非递归实现.斐波那契数列生成器: \[ \begin{equation} F(n)= \begin{cases} n & n=0, 1\\ F(n ...

  2. fibnacci数列递归实现

    斐波那契数列 Fibonacci sequence又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为"兔子数列" ...

  3. 【简洁之美】裴波那切数列生成器 python

    裴波那切数列可以用生成器较好的去生成,直接上代码: # 1 控制最大数字版本 def fib(max): x,y = 0,1 while y < max: yield x x,y = y,x+y ...

  4. fibnacci数列的两种实现（递归实现和循环实现）

    //一切尽在规律中,认真观察,你会明白更多... using System;using System.Collections.Generic;using System.Linq;using Syste ...

  5. vijos - P1543极值问题(斐波那契数列 + 公式推导 + python)

    P1543极值问题 Accepted 标签:[显示标签] 背景 小铭的数学之旅2. 描写叙述 已知m.n为整数,且满足下列两个条件: ① m.n∈1,2.-,K ② (n^ 2-mn-m^2)^2＝1 ...

  6. fibnacci数列递归

    1,斐波那契数列(Fibonacci sequence),又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这 ...

  7. look and say 外观数列的python实现

    #look_and_say 外观数列 如果我们把 1 作为Look-and-say 数列的第一项,那么,它的前几项是这样的: 1, 11, 21, 1211, 111221, 312211, 1311 ...

  8. fibnacci数列

    斐波那契数列(Fibonacci sequence),又称黄金分割数列.因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为"兔子数列&qu ...

  9. 青蛙跳台阶问题（斐波那契数列） python

    一只青蛙一次可以跳上1级台阶,也可以跳上2级.求该青蛙跳上一个n级的台阶总共有多少种跳法 class Solution: def jump(self,n): if n ==0: return 0 el ...

随机推荐

  1. Java高并发下多线程编程

    1.创建线程 Java中创建线程主要有三种方式: 继承Thread类创建线程类: 定义Thread类的子类,并重写该类的run方法,该run方法的方法体就代表了线程要完成的任务.因此也把run方法称为 ...

  2. vector概述

    vector是一个能够支持任何类型的容器,本身为一个可以动态增长的数组. 1.vector基本数据结构 STL中所有的容器都包括三部分: 迭代器,遍历容器的元素,控制容器空间的边界和元素移动. 构造函 ...

  3. js 每日一更（数组转换成前端更容易解析的树状结构）

    <!DOCTYPE html> <html> <head> <meta http-equiv="content-type" content ...

  4. mysql连接出错：ERROR 1040 (HY000): Too many connections

    1.查看mysql的最大连接数:show variables like '%max_connections%';  2. 查看服务器响应的最大连接数: 3. 设置最大连接数: set GLOBAL m ...

  5. Mybatis返回插入数据的主键的两种方式

    方式一: 需要在映射文件中添加如下片段: <insert id="insertProduct" parameterType="domain.model.Produc ...

  6. new方法实现原理

    new方法实现原理 完整的创建一个可用的对象:Person *p=[Person new]; new方法的内部会分别调用两个方法来完成3件事情: (1)使用alloc方法来分配存储空间(返回分配的对象 ...

  7. jdk1.5新特性之-----自动装箱与自动拆箱

    import java.util.ArrayList; /* jdk1.5新特性之-----自动装箱与自动拆箱. java是面向对象 的语言,任何事物都可以使用类进行描述,sun就使用了 一些类描述j ...

  8. .NET6: 开发基于WPF的摩登三维工业软件 (2)

    在<.NET6: 开发基于WPF的摩登三维工业软件 (1)>我们创建了一个"毛坯"界面,距离摩登还差一段距离.本文将对上一阶段的成果进行深化,实现当下流行的暗黑风格UI ...

  9. 经常使用的系统类Math、Arrays、System、BigInteger和BigDecimal以及日期类，时间戳

    一.Math 常用类: //看看Math常用的方法(静态方法)//1.abs绝对值int abs = Math . abs(-9);System. out . printLn(abs);//9//2. ...

  10. Pandas常用操作 - 去重

    1. 使用 drop_duplicates 去重 1.1 初始化数据 df = pd.DataFrame({'stu_name': ['Tom', 'Tony', 'Jack', 'Jack', np ...