绵阳2020CCPC补题

绵阳2020CCPC D,K,J,L,G

D. Defuse the Bombs

知识点：二分答案

复杂度：\(O(nlogn+log^2n)\)

vp时我猜了一个结论，验了几个样例就写了，喜提WA3

然后队友写了二分答案复杂度\(O(log^2n)\)，也WA3

然后队友发现是二分边界错了，改了后AC

反思：这题WA的两发都是可以避免的，即没判断更多的样例，也没计算二分上界

先排序求一个前缀和

二分答案后进行判断当前答案 \(ans\)

在 a 数组中二分得到第一个比x小的位置

那么 \(ans\) 是否可行即比较 \(pre[i] + x\) 与 \(i*x\) 的大小

---

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;

const int N = 1e5 + 5;

int n;
int a[N];
ll pre[N];

bool check(ll x)
{
    auto it = upper_bound(a + 1, a + n + 1, x) - a - 1;
    return pre[it] + x >= it * x;
}

void solve()
{
    cin >> n;
    rep(i, 1, n) cin >> a[i];
    sort(a + 1, a + n + 1);
    rep(i, 1, n) pre[i] = pre[i - 1] + a[i];
    ll l = 0, r = 2e9 + 10, mid;
    while (l < r)
    {
        mid = (l + r + 1) >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    cout << l + 1 << endl;
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}

---

K. Knowledge is Power

知识点：构造

复杂度：\(O(1)\)

该题思路出的很快，并且也排除了几个错误情况，但是还是没有完全验证正确性，导致WA一发，耐下心来这一发也可以避免的

一点点失误累积可能就会成为下次名落孙山的原因了

明显当 n 为奇数时可以拆成 \(\frac{n-1}{2}\) 与 \(\frac{n+1}{2}\)

当 n 为偶数时，我们讨论 \(\frac{n}{2}\) 的奇偶

1. 当 \(\frac{n}{2}\) 为偶数时
   
   显然可以拆成 \(\frac{n}{2}-1\) 与 \(\frac{n}{2}+1\)
2. 当 \(\frac{n}{2}\) 为奇数时
   
   拆成 \(\frac{n}{2}-2\) 与 \(\frac{n}{2}+2\) 显然是一种合法情况
   
   所以该情况答案的上界就为 4
   
   样例贴心的给出了反例，什么良心出题人
   
   此时显然 n 不可能拆成多于 3 个数
   
   而 n 拆成 3 个数的情况显然固定
   1. n % 3 == 0
      
      n 可以拆成 \(\frac{n}{3}-1\) ， \(\frac{n}{3}\) ， \(\frac{n}{3}+1\)
   2. n % 3 == 1
      
      n 可以拆成 \(\frac{n-1}{3}-1\) ， \(\frac{n-1}{3}\) ， \(\frac{n-1}{3}+2\)
   3. n % 3 == 2
      
      n 可以拆成 \(\frac{n+1}{3}-2\) ， \(\frac{n+1}{3}\) ， \(\frac{n+1}{3}+1\)

直接判断3个数是否互质即可

样例甚至贴心的给出了唯一不可能的情况，他真的，我哭死

---

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;

int n;

void solve()
{
    cin >> n;
    if (n % 2) cout << 1 << endl;
    else if (n == 6) cout << -1 << endl;
    else if ((n / 2) % 2 == 0) cout << 2 << endl;
    else
    {
        bool ok = false;
        if (n % 3 == 1)
        {
            if ((n / 3) % 2 && (n / 3 - 1) % 3) ok = true;
        }
        else if (n % 3 == 2)
        {
            if (((n + 1) / 3) % 2 && (n / 3 - 1) % 3) ok = true;
        }
        else
        {
            if ((n / 3) % 2 == 0)
            {
                cout << 2 << endl;
                return;
            }
        }
        cout << (ok ? 3 : 4) << endl;
    }
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}

---

J. Joy of Handcraft

知识点：线段树 / 并查集

复杂度：\(O(mlog^2m)/O(mlogm)\)

这题一开始就验了线段树复杂度是对的，

但是队友线段树懒惰标记忘记清空导致一直没过样例，

线段树的bug还特别难找，熟练度还是低了

调了整整1个小时，虽然1发过

显然当 \(t\) 相同时 只保留最大的 \(x\) 即可

那么对于所有的 \(t=1,2,3,...,n\) 只会有1个答案

如果用线段树更新区间，那么所有的线段个数为 \(\frac{n}{2}+\frac{n}{3}+\frac{n}{4}+...+\frac{n}{n}\)

总和为 \(nlogn\), 乘上线段树区间修改的复杂度为 \(logn\)，

总复杂度为 \(O(nlog^2n)\)

看了题解后发现还有并查集写法，具体操作就是并查集维护当前位置向后第一个没被染色的点

然后对染色区间的 \(x_i\) 从大到小排序，染完一个区间就将当前区间删除，染色次数就不会超过 \(O(m)\)

说来惭愧，写过原题却一点没印象

顺带一提，如果 \(ti>m\) 记得让 \(ti=min(ti,m)\)

否则很可能 RE 或者 WA

队友在debug到神志不清的时候把范围全改成1e5，导致一发过

这也在你的预料之中吗.jpg

---

线段树写法

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
#define fi first
#define se second
#define pii pair<int,int>
template<class T> using vc = vector<T>;

const int N = 1e5 + 5;

int n, m;

struct Segment_Tree
{
    struct P
    {
        int l, r;
        // 懒惰标记
        ll lazy;
    } p[N << 2];
    void init_lazy(int id)
    {
        /* 初始化懒惰标记 */
        p[id].lazy = 0;
    }
    void union_lazy(int fa, int ne)
    {
        /* 合并父子标记 */
        p[ne].lazy = p[fa].lazy;
    }
    void cal_lazy(int fa, int ne)
    {
        /* 用父亲标记修改当子区间 */
    }
    void push_down(int id)
    {
        if (p[id].lazy/* 判断是否有懒惰标记 */)
        {
            if (p[id].l != p[id].r)
            {
                int ne = id << 1;
                cal_lazy(id, ne);
                cal_lazy(id, ne + 1);
                union_lazy(id, ne);
                union_lazy(id, ne + 1);
            }
            init_lazy(id);
        }
    }
    void update(int id)
    {
        int ne = id << 1;
        /* 合并左右子树 */
    }
    void build(int id, int l, int r)
    {
        p[id].l = l;
        p[id].r = r;
        init_lazy(id);
        if (l == r)
        {
            /* 初始化单点区间信息 */
            return;
        }
        int mid = (l + r) >> 1;
        int ne = id << 1;
        build(ne, l, mid);
        build(ne + 1, mid + 1, r);
        update(id);
    }
    void change(int id, int l, int r, ll d)
    {
        push_down(id);
        if (l <= p[id].l && p[id].r <= r)
        {
            /* 修改懒惰标记 */
            p[id].lazy = d;
            cal_lazy(id, id);
            return;
        }
        int mid = (p[id].l + p[id].r) >> 1;
        int ne = id << 1;
        if (r <= mid) change(ne, l, r, d);
        else if (l > mid) change(ne + 1, l, r, d);
        else
        {
            change(ne, l, r, d);
            change(ne + 1, l, r, d);
        }
        update(id);
    }
    P sum(int id, int l, int r)
    {
        if (p[id].lazy) return p[id];
        if (l <= p[id].l && p[id].r <= r) return p[id];
        int mid = (p[id].l + p[id].r) >> 1;
        int ne = id << 1;
        if (r <= mid) return sum(ne, l, r);
        return sum(ne + 1, l, r);
    }
}T;

void solve()
{
    cin >> n >> m;
    T.build(1, 1, m);
    vc<int> t(m + 1);
    rep(i, 1, n)
    {
        int ti, xi; cin >> ti >> xi;
        ti = min(ti, m);
        t[ti] = max(t[ti], xi);
    }
    vc<pii> p;
    rep(i, 1, m) if (t[i]) p.emplace_back(t[i], i);
    sort(p.begin(), p.end());
    for (auto u : p)
        for (int i = 1; i <= m; i += u.se * 2)
            T.change(1, i, min(m, i + u.se - 1), u.fi);
    rep(i, 1, m) cout << T.sum(1, i, i).lazy << " \n"[i == m];
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}

并查集写法

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l,_##i=r;i<=_##i;i++)
#define per(i,r,l) for(int i=r,_##i=l;i>=_##i;i--)
#define ll long long
#define fi first
#define se second
#define pii pair<int,int>
template<class T> using vc = vector<T>;

const int mod = 1e9 + 7;
const int N = 1e5 + 5;

int n, m, k;

int f[N];

void bcj_init(int n) { iota(f, f + n + 1, 0); }

int find(int u)
{
    if (f[u] == u)return u;
    return f[u] = find(f[u]);
}

void solve()
{
    cin >> n >> m;
    bcj_init(m + 1);
    vc<int> t(m + 1);
    rep(i, 1, n)
    {
        int ti, xi; cin >> ti >> xi;
        ti = min(ti, m);
        t[ti] = max(t[ti], xi);
    }
    vc<pii> p;
    rep(i, 1, m) if (t[i]) p.emplace_back(t[i], i);
    sort(p.begin(), p.end(), greater<pii>());
    vc<int> ans(m + 1);
    for (auto u : p)
    {
        for (int i = 1; i <= m; i += u.se * 2)
        {
            int x = find(i), r = min(m, i + u.se - 1);
            while (x <= r)
            {
                ans[x] = u.fi;
                f[x] = x + 1;
                x = find(x);
            }
        }
    }
    rep(i, 1, m) cout << ans[i] << " \n"[i == m];
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}

---

L. Lottery

知识点：多重背包，找规律

复杂度：\(O(nlog^2n+nlogn)\) 优化后 \(O(nlogn)\)

这题其实很快就有思路了，但是队友卡在上一题的线段树太久了，导致一直没占到电脑

然后在拿到电脑时，一开始的写法让map的指针乱指导致怒WA一发

后来增加一点常数去掉了乱七八糟的指针就一发AC

• 观察样例1我们可以得到，如果每种 \(2^i\) 只有1个，那么答案明显是 \(2^n\)
• 如果数据范围比较小明显就是一个多重背包，但是该题的范围是1e9
• 那么按照多重背包的优化，我们将每一对 \(a_i\) 与 \(x_i\) 进行拆分
  
  例如 \(a_i=2\) 与 \(x_i = 3\) 我们就拆成 \(2^2\) 与 \(2^3\)
  
  换句话说就是，当 \(x_i>=(1<<k)-1\) 时就拆出 \((111...11)_{01}\)
• 当全部拆完时，对于每一位 \(2^{a_i}\) 在该位保留1 的情况下向 \(2^{a_i+1}\) 进位
• 处理完进位后，对于每一位 \(2^{a_i}\)，\(x_i\) 要么为 1，要么为2
• 对于不连续的 \(a_i\) 明显是乘法原则计数
  • 对于连续的 \(a_i\) 如果该位为 1，则方案数为后缀方案数 × 2 × 前缀方案数
  • 对于连续的 \(a_i\) 如果该位为 2，则方案数为后缀方案数 × (2 × 前缀方案数 + 1)
  • 举例来说就是 \(12121\) 的方案数为 \(2×(2×2×(2×2+1)+1)\)

明显我们从后向前枚举 \(2^{a_i}\) 更方便计算

---

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define per(i,r,l) for(int i=r;i>=l;i--)
#define ll long long
#define fi first
#define se second
template<class T> using vc = vector<T>;

const int mod = 1e9 + 7;
const int N = 1e5 + 5;

int n, m, k;
map<int, int> mp;

void calc()
{
    int a, x;
    cin >> a >> x;
    while (x)
    {
        auto &it = mp[a++];
        x += it;
        it = (x - 1) % 2 + 1;
        x = (x - 1) / 2;
    }
}

void solve()
{
    mp.clear();
    cin >> n;
    rep(i, 1, n) calc();
    ll ans = 1, tmp = 1;
    for (auto it = mp.rbegin(); it != mp.rend(); it++)
    {
        if (it->se == 1) tmp = tmp * 2 % mod;
        else tmp = (tmp * 2 + 1) % mod;
        auto ne = next(it);
        if (ne == mp.rend())
        {
            ans = ans * tmp % mod;
            break;
        }
        if (ne->fi + 1 != it->fi)
        {
            ans = ans * tmp % mod;
            tmp = 1;
        }
    }
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}

优化后

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l,_##i=r;i<=_##i;i++)
#define per(i,r,l) for(int i=r,_##i=l;i>=_##i;i--)
#define ll long long
#define fi first
#define se second
#define pii pair<int,int>
template<class T> using vc = vector<T>;

const int mod = 1e9 + 7;
const int N = 1e5 + 5;

int n, m, k;

pii a[N];

void solve()
{
    cin >> n;
    rep(i, 1, n) cin >> a[i].fi >> a[i].se;
    sort(a + 1, a + n + 1);
    vc<pii> p;
    ll tmp(0);
    rep(i, 1, n)
    {
        ll now = a[i].fi;
        tmp += a[i].se;
        if (i == n)
        {
            while (tmp)
            {
                p.emplace_back(now++, (tmp - 1) % 2 + 1);
                tmp = (tmp - 1) / 2;
            }
        }
        else
        {
            while (tmp && now != a[i + 1].fi)
            {
                p.emplace_back(now++, (tmp - 1) % 2 + 1);
                tmp = (tmp - 1) / 2;
            }
        }
    }
    ll ans = 1, len = p.size() - 1; tmp = 1;
    per(i, len, 0)
    {
        if (p[i].se == 1) tmp = tmp * 2 % mod;
        else tmp = (tmp * 2 + 1) % mod;
        if (!i || p[i].fi != p[i - 1].fi + 1)
        {
            ans = ans * tmp % mod;
            tmp = 1;
        }
    }
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}

---

G. Game of Cards

vp时没写出来的题，结论猜错了，果然博弈题还是要打表看sg函数

先打个表

---

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)

array<int, 4> c;
const int sz = 7;

int dp[sz + 1][sz + 1][sz + sz / 2 + 1][2];

bool brute()
{
    function<bool(array<int, 4>)> dfs = [&](array<int, 4> c) -> bool
    {
        auto &u = dp[c[0]][c[1]][c[2]][c[3]];
        if (~u) return u;
        bool ok = true;
        if (c[0] >= 2) ok &= dfs({ c[0] - 1,c[1],c[2],c[3] });
        if (c[0] && c[1] + c[2] + c[3]) ok &= dfs({ c[0] - 1,c[1],c[2],c[3] });
        if (c[1] >= 2) ok &= dfs({ c[0],c[1] - 2,c[2] + 1,c[3] });
        if (c[1] && c[2]) ok &= dfs({ c[0],c[1] - 1,c[2] - 1,c[3] | 1 });
        return u = !ok;
    };
    return dfs(c);
}

void solve()
{
    memset(dp, -1, sizeof(dp));
    rep(i, 0, sz) rep(i1, 0, sz) rep(i2, 0, sz) rep(i3, 0, 1)
    {
        c = { i,i1,i2,i3 };
        brute();
    }
    rep(i, 0, sz) rep(i1, 0, sz)
    {
        cout << string(i1, ' ');
        rep(i2, 0, sz) cout << dp[i][i1][i2][0] << dp[i][i1][i2][1] << " \n"[i2 == sz];
    }
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    solve();
}

00 00 00 00 00 00 00 00
 00 11 11 11 11 11 11 11
  11 11 11 11 11 11 11 11
   00 00 00 00 00 00 00 00
    00 11 11 11 11 11 11 11
     11 11 11 11 11 11 11 11
      00 00 00 00 00 00 00 00
       00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
 11 00 00 00 00 00 00 00
  00 00 11 11 11 11 11 11
   11 11 11 11 11 11 11 11
    11 00 00 00 00 00 00 00
     00 00 11 11 11 11 11 11
      11 11 11 11 11 11 11 11
       11 00 00 00 00 00 00 00
10 00 00 00 00 00 00 00
 00 11 11 11 11 11 11 11
  11 11 11 11 11 11 11 11
   00 00 00 00 00 00 00 00
    00 11 11 11 11 11 11 11
     11 11 11 11 11 11 11 11
      00 00 00 00 00 00 00 00
       00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
 11 00 00 00 00 00 00 00
  00 00 11 11 11 11 11 11
   11 11 11 11 11 11 11 11
    11 00 00 00 00 00 00 00
     00 00 11 11 11 11 11 11
      11 11 11 11 11 11 11 11
       11 00 00 00 00 00 00 00
10 00 00 00 00 00 00 00
 00 11 11 11 11 11 11 11
  11 11 11 11 11 11 11 11
   00 00 00 00 00 00 00 00
    00 11 11 11 11 11 11 11
     11 11 11 11 11 11 11 11
      00 00 00 00 00 00 00 00
       00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
 11 00 00 00 00 00 00 00
  00 00 11 11 11 11 11 11
   11 11 11 11 11 11 11 11
    11 00 00 00 00 00 00 00
     00 00 11 11 11 11 11 11
      11 11 11 11 11 11 11 11
       11 00 00 00 00 00 00 00
10 00 00 00 00 00 00 00
 00 11 11 11 11 11 11 11
  11 11 11 11 11 11 11 11
   00 00 00 00 00 00 00 00
    00 11 11 11 11 11 11 11
     11 11 11 11 11 11 11 11
      00 00 00 00 00 00 00 00
       00 11 11 11 11 11 11 11
01 11 11 11 11 11 11 11
 11 00 00 00 00 00 00 00
  00 00 11 11 11 11 11 11
   11 11 11 11 11 11 11 11
    11 00 00 00 00 00 00 00
     00 00 11 11 11 11 11 11
      11 11 11 11 11 11 11 11
       11 00 00 00 00 00 00 00

---

• 明显当 \(c_2>=2\) 时的规律十分好找
  
  当 \(c_2>=2\) 时，\(c_0\%2==c_1\%3\) 时，先手必败

• 现在来看 \(c_2<2\) 时的情况

  • \(c_0\),0,0,0 时，当 \(c_0\) 为奇数或者等于 0 时，先手必败
  • \(c_2==0\) 时
    • \(c_0\) 为偶数时，\(c_1\%3!=2\) 先手必败
    • \(c_0\) 为奇数时，\(c_1\%3==2\) 先手必败
  • \(c_2==1\) 时
    • \(c_0\) 为偶数时，\(c_1\%3==0\) 先手必败
    • \(c_0\) 为奇数时，\(c_1\%3!=0\) 先手必败

---

#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define ll long long
template<class T> using vc = vector<T>;

const int N = 1e5 + 5;

int n;
array<int, 4> c;

void pr(bool fi_win)
{
    cout << (fi_win ? "Rabbit" : "Horse") << endl;
}

void solve()
{
    rep(i, 0, 3) cin >> c[i];
    if (c[2] >= 2) pr(c[0] % 2 != c[1] % 3);
    else if (!c[1] && !c[2] && !c[3]) pr(c[0] % 2 == 0 && c[0]);
    else if (c[2])
    {
        if (c[0] % 2) pr(c[1] % 3 == 0);
        else pr(c[1] % 3);
    }
    else
    {
        if (c[0] % 2) pr(c[1] % 3 != 2);
        else pr(c[1] % 3 == 2);
    }
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}

---

H. Hide and Seek

知识点：分类讨论

复杂度：\(O(1)\)

赛时甚至没看到这题，题解说的挺清楚的，确实不画图根本想不全

---

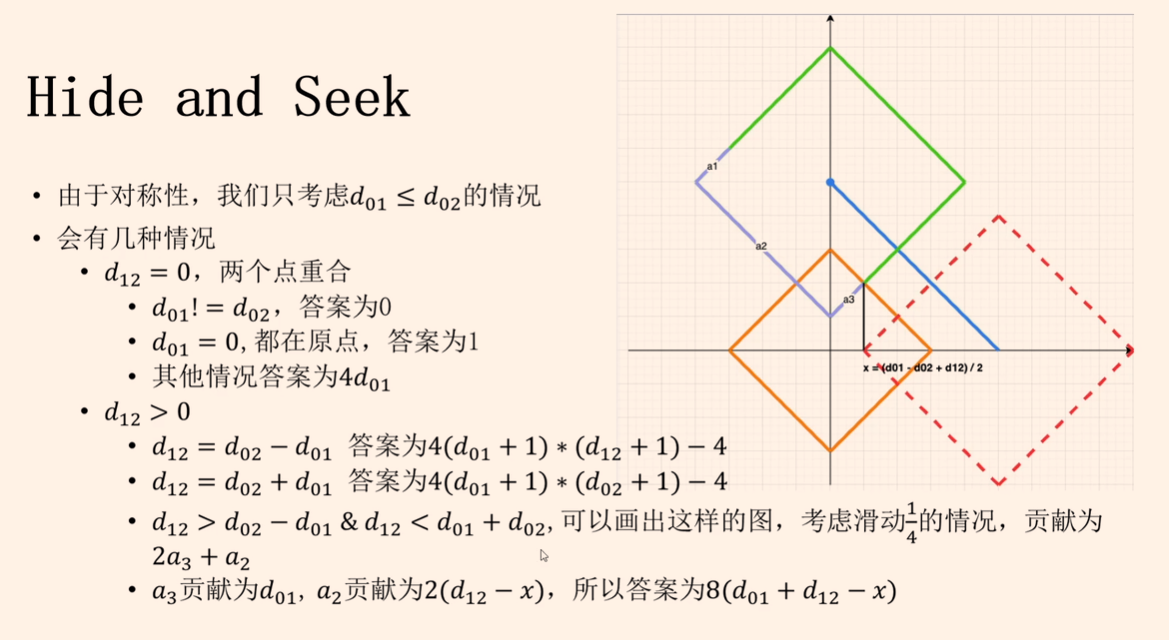
#include<bits/stdc++.h>
using namespace std;
#define rep(i,l,r) for(int i=l,_##i=r;i<=_##i;i++)
#define per(i,r,l) for(int i=r,_##i=l;i>=_##i;i--)
#define ll long long
template<class T> using vc = vector<T>;

void solve()
{
    ll d01, d02, d12, ans(0);
    cin >> d01 >> d02 >> d12;
    if (d01 > d02) swap(d01, d02);
    if (d12 == 0)
    {
        if (d01 != d02) ans = 0;
        else if (!d01) ans = 1;
        else ans = 4 * d01;
    }
    else if (d12 == d02 - d01) ans = (d01 + 1) * 4 * (d12 + 1) - 4;
    else if (d12 == d02 + d01) ans = (d01 + 1) * 4 * (d02 + 1) - 4;
    else if (d12 > d02 - d01 && d12 < d01 + d02)
    {
        if ((d02 - d12 - d01) % 2) ans = 0;
        else
        {
            ll x = (d01 - d02 + d12) / 2;
            ans = 8 * (d01 + d12 - x);
        }
    }
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    int T = 1;
    cin >> T;
    rep(i, 1, T)
    {
        cout << "Case #" << i << ": ";
        solve();
    }
}