POJ 3522 ——Slim Span——————【最小生成树、最大边与最小边最小】

Slim Span

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 7102		Accepted: 3761

Description

Given an undirected weighted graph G, you should find one of spanning trees specified as follows.

The graph G is an ordered pair (V, E), where V is a set of vertices {v₁, v₂, …, v_n} and E is a set of undirected edges {e₁, e₂, …, e_m}. Each edge e ∈ E has its weight w(e).

A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n − 1 edges. The slimness of a spanning tree T is defined as the difference between the largest weight and the smallest weight among the n − 1 edges of T.

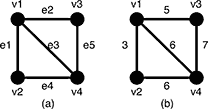
Figure 5: A graph G and the weights of the edges

For example, a graph G in Figure 5(a) has four vertices {v₁, v₂, v₃, v₄} and five undirected edges {e₁, e₂, e₃, e₄, e₅}. The weights of the edges are w(e₁) = 3, w(e₂) = 5, w(e₃) = 6, w(e₄) = 6, w(e₅) = 7 as shown in Figure 5(b).

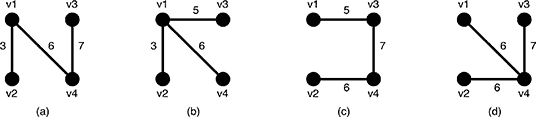
Figure 6: Examples of the spanning trees of G

There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning tree T_a in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the tree T_a is 4. The slimnesses of spanning trees T_b, T_c and T_d shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1.

Your job is to write a program that computes the smallest slimness.

Input

The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.

n	m
a1	b1	w1
	⋮
am	bm	wm

Every input item in a dataset is a non-negative integer. Items in a line are separated by a space. n is the number of the vertices and m the number of the edges. You can assume 2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2. a_k and b_k (k = 1, …,m) are positive integers less than or equal to n, which represent the two vertices v_ak and v_bk connected by the kth edge e_k. w_k is a positive integer less than or equal to 10000, which indicates the weight of e_k. You can assume that the graph G = (V, E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices).

Output

For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, −1 should be printed. An output should not contain extra characters.

Sample Input

4 5
1 2 3
1 3 5
1 4 6
2 4 6
3 4 7
4 6
1 2 10
1 3 100
1 4 90
2 3 20
2 4 80
3 4 40
2 1
1 2 1
3 0
3 1
1 2 1
3 3
1 2 2
2 3 5
1 3 6
5 10
1 2 110
1 3 120
1 4 130
1 5 120
2 3 110
2 4 120
2 5 130
3 4 120
3 5 110
4 5 120
5 10
1 2 9384
1 3 887
1 4 2778
1 5 6916
2 3 7794
2 4 8336
2 5 5387
3 4 493
3 5 6650
4 5 1422
5 8
1 2 1
2 3 100
3 4 100
4 5 100
1 5 50
2 5 50
3 5 50
4 1 150
0 0

Sample Output

1
20
0
-1
-1
1
0
1686
50

Source

Japan 2007

 

 

题目大意：让你求一个生成树，树边的最大值跟最小值的差值最小。

 

解题思路：其实就是kruskal求最小生成树。暴力枚举不同的最小边。

 

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<iostream>
using namespace std;
const int maxn = 110;
const int maxe = 11010;
struct Edge{
    int from,to,dist,idx;
    Edge(){}
    Edge(int _from,int _to,int _dist,int _idx):from(_from),to(_to),dist(_dist),idx(_idx){}
}edges[maxe];
struct Set{
    int pa,rela;
}sets[maxn];
int ans[maxn];
bool cmp(Edge a,Edge b){
    return a.dist < b.dist;
}
void init(int n){
    for(int i = 0; i <= n; i++){
        sets[i].pa =  i;
    }
}
int Find(int x){
    if(x == sets[x].pa){
        return x;
    }
    int tmp = sets[x].pa;
    sets[x].pa = Find(tmp);
    return sets[x].pa;
}
int main(){
    int n, m;
    while(scanf("%d%d",&n,&m)!=EOF&&(n+m)){
        init(n);
        int a,b,c;
        for(int i = 0; i < m; i++){
            scanf("%d%d%d",&a,&b,&c);
            edges[i] = Edge(a,b,c,i);
        }
        sort(edges,edges+m,cmp);
        int pos = 0 , cnt = 0;
        for(int i = 0; i < m; i++){
            Edge & e = edges[i];
            int rootx, rooty;
            rootx = Find(e.from);
            rooty = Find(e.to);
            if(rootx == rooty){
                continue;
            }
            cnt++;
            sets[rooty].pa = rootx;
            pos = i;
        }
        if(cnt != n - 1){
            puts("-1");
            continue;
        }
        int ans = edges[pos].dist - edges[0].dist;
        for(int j = 1; j <= m - n + 1; j++){
            cnt = 0;
            for(int i = 0; i <= n; i++){
                sets[i].pa = i;
            }
            for(int i = j; i < m; i++){
                Edge & e = edges[i];
                int rootx, rooty;
                rootx = Find(e.from);
                rooty = Find(e.to);
                if(rootx == rooty) {
                    continue;
                }
                sets[rooty].pa = rootx;
                cnt++;
                pos = i;
            }
            if(cnt < n-1){
                break;
            }else{
                int tmp = edges[pos].dist - edges[j].dist;
                ans = min(ans,tmp);
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}