机器学习：逻辑回归（scikit-learn 中的逻辑回归）

一、基础理解

• 使用逻辑回归算法训练模型时，为模型引入多项式项，使模型生成不规则的决策边界，对非线性的数据进行分类；

• 问题：引入多项式项后，模型变的复杂，可能产生过拟合现象；

• 方案：对模型正则化处理，损失函数添加正则项（αL₂），生成新的损失函数，并对新的损失函数进行优化；

• 优化新的损失函数：

1. 满足了让原来的损失函数尽量的小；
2. 另一方面，对于 L₂ 正则项（包含参数 θ 值），限制 θ 的大小；
3. 引入了参数 α ，调节新的损失函数中两部分（原损失函数和 L₂ 正则项）的重要程度；当然也可以引入 αL₁ 正则项；

二、正则化的其它方式

• 新的表达正则化的方式：只是方式不同，正则化的原来一样；
• 

1. 改变了超参数的位置：α、C；
2. 如果超参数 C 越大，原损失函数 J(θ) 的地位相对较重要，优化损失函数时主要集中优化 J(θ) ，使其减少到最小；
3. 如果超参数 C 非常小，正则项 L₂ 的地位相对较重要，优化损失函数时主要集中优化 L₂ ，使参数 θ 中的元素尽量的小；
4. 如果想让使正则项不重要，需要增大参数 C；

• 其实在 J(θ) 前加参数 C，相当于将原来的 αL₂ 变为 1/αL₂ ，两中方式等效；

• α、C：平衡新的损失函数中两部分的关系；

• 在逻辑回归、SVM算法中，更偏好使用 C.J(θ) + L₂ 的方式；scikit-learn 的逻辑回归算法中，也是使用此方式；

1. 原因：使用 C.J(θ) + L₂ 方式时，正则项的系数为 1，也就是说优化算法模型时不得不使用正则化；

三、思考

• 多项式回归：假设在特征空间中，样本的分布规律呈多项式曲线状态，可能类似 2 次多项式曲线，也可能是 3 次多项式的曲线，也可能是 n 次多项式的曲线；

1. n 次多项式曲线：y = xⁿ + ...，最高 n 次方，还有其他很多项，x 与 y 的关系曲线；

• 疑问1：是不是二维空间的所有不规则曲线都存在一个多项式与其对应？

• 疑问2：如果样本分布规律不是多项式曲线的规律，再使用多项式回归算法，或者逻辑回归的多项式形式进行分类，是不是就不准确？

• 思考：解决具体的问题，通过可视化查看样本相根据特征大致的分布，再判断可以使用哪些算法，组个尝试，找个最合适的一个；

1. 最合适：准确度高、效率高；

四、实例scikit-learn中的逻辑回归算法

• scikit-learn中的逻辑回归算法自动封装了模型的正则化的功能，只需要调整 C 和 penalty；
• 主要参数：degree、C、penalty；（还有其它参数）

　1）直接使用逻辑回归算法

• import numpy as np
  import matplotlib.pyplot as plt
  
  np.random.seed(666)
  X = np.random.normal(0, 1, size=(200, 2))
  y = np.array(X[:,0]**2 + X[:,1] < 1.5,dtype='int')
  
  # 随机抽取 20 个样本，让其分类为 1，相当于认为更改数据，添加噪音
  for _ in range(20):
      y[np.random.randint(200)] = 1
  
  plt.scatter(X[y==0,0], X[y==0,1])
  plt.scatter(X[y==1,0], X[y==1,1])
  plt.show()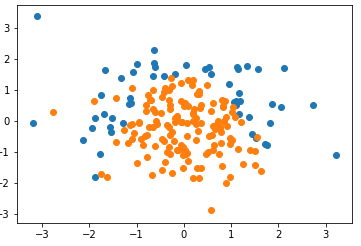

  

• 为虚拟的测试数据设置种子 666：则每次执行 np.random.normal(0, 1, size=(200, 2)) 时，随机生成的 X 不变；
• 随机生成数据是系统内定的，随机种子是系统随机生成数据时的依据，只要设定的随机种子相同，所有人生成的数据一样；（待考察）

• from sklearn.model_selection import train_test_split
  
  X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
  
  from sklearn.linear_model import LogisticRegression
  
  log_reg = LogisticRegression()
  log_reg.fit(X_train, y_train)
  # LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
            intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1,
            penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
            verbose=0, warm_start=False)

1. C=1.0：默认超参数 C 的值为1.0；

2. penalty='l2'：默认使用 L2 正则项；

• def plot_decision_boundary(model, axis):
  
      x0, x1 = np.meshgrid(
          np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
          np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
      )
      X_new = np.c_[x0.ravel(), x1.ravel()]
  
      y_predict = model.predict(X_new)
      zz = y_predict.reshape(x0.shape)
  
      from matplotlib.colors import ListedColormap
      custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
  
      plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
  
  plot_decision_boundary(log_reg, axis=[-4, 4, -4, 4])
  plt.scatter(X[y==0,0], X[y==0,1])
  plt.scatter(X[y==1,0], X[y==1,1])
  plt.show()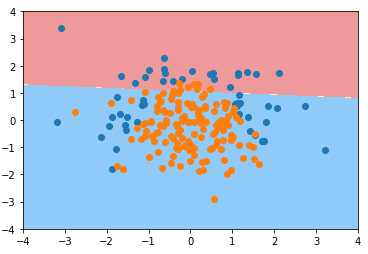

  

　2）为逻辑回归算法的模型添加多项式项

• degree = 2、C 默认1.0

  from sklearn.pipeline import Pipeline
  from sklearn.preprocessing import PolynomialFeatures
  from sklearn.preprocessing import StandardScaler
  
  def PolynomialLogisticRegression(degree):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std_scaler', StandardScaler()),
          ('log_reg', LogisticRegression())
      ])
  
  # 使用管道时，先生成实例的管道对象，在进行 fit；
  poly_log_reg = PolynomialLogisticRegression(degree=2)
  poly_log_reg.fit(X_train, y_train)
  
  plot_decision_boundary(poly_log_reg, axis=[-4, 4, -4, 4])
  plt.scatter(X[y==0,0], X[y==0,1])
  plt.scatter(X[y==1,0], X[y==1,1])
  plt.show()

  

• degree = 20、C 默认1.0

  poly_log_reg2 = PolynomialLogisticRegression(degree=20)
  poly_log_reg2.fit(X_train, y_train)
  
  plot_decision_boundary(poly_log_reg2, axis=[-4, 4, -4, 4])
  plt.scatter(X[y==0,0], X[y==0,1])
  plt.scatter(X[y==1,0], X[y==1,1])
  plt.show()

  

• degree = 20、C = 0.1

  def PolynomialLogisticRegression(degree, C):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std_scaler', StandardScaler()),
          ('log_reg', LogisticRegression(C=C))
      ])
  
  poly_log_reg3 = PolynomialLogisticRegression(degree=20, C=0.1)
  poly_log_reg3.fit(X_train, y_train)
  
  plot_decision_boundary(poly_log_reg3, axis=[-4, 4, -4, 4])
  plt.scatter(X[y==0,0], X[y==0,1])
  plt.scatter(X[y==1,0], X[y==1,1])
  plt.show()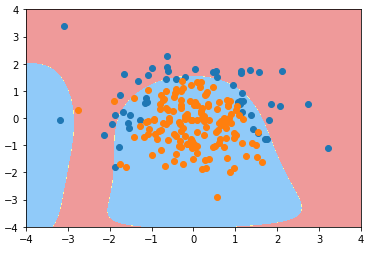

  

• degree = 20、C = 0.1、penalty = 'L1'（penalty：正则项类型， 默认为 L2）

  def PolynomialLogisticRegression(degree, C, penalty='l2'):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std_scaler', StandardScaler()),
          ('log_reg', LogisticRegression(C=C, penalty=penalty))
      ])
  
  poly_log_reg4 = PolynomialLogisticRegression(degree=20, C=0.1, penalty='l1')
  poly_log_reg4.fit(X_train, y_train)
  
  plot_decision_boundary(poly_log_reg4, axis=[-4, 4, -4, 4])
  plt.scatter(X[y==0,0], X[y==0,1])
  plt.scatter(X[y==1,0], X[y==1,1])
  plt.show()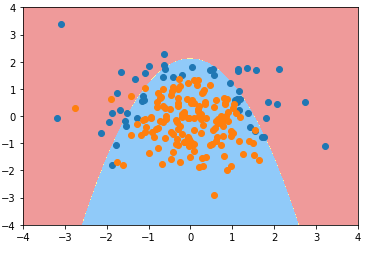

  

1. 分析：degree = 20，模型的决策边界太复杂，模型可能过拟合，使用 L1 正则项进行模型的正则化；
2. 分析2：模型过拟合后，有很多多项式项，使用 L1 正则项，使得这些多项式项的系数为 0，进而使模型决策边界更加规则，不会弯弯曲曲，便于可视化；