P4768 [NOI2018]归程

\(\color{#0066ff}{题目描述}\)

本题的故事发生在魔力之都，在这里我们将为你介绍一些必要的设定。 魔力之都可以抽象成一个 n 个节点、m 条边的无向连通图（节点的编号从 1 至 n）。我们依次用 l,a 描述一条边的长度、海拔。 作为季风气候的代表城市，魔力之都时常有雨水相伴，因此道路积水总是不可避免 的。由于整个城市的排水系统连通，因此有积水的边一定是海拔相对最低的一些边。我们用水位线来描述降雨的程度，它的意义是：所有海拔不超过水位线的边都是有积水的。

Yazid 是一名来自魔力之都的OIer，刚参加完ION2018 的他将踏上归程，回到他 温暖的家。 Yazid 的家恰好在魔力之都的 1 号节点。对于接下来 Q 天，每一天Yazid 都会告诉你他的出发点 v ，以及当天的水位线p。 每一天，Yazid 在出发点都拥有一辆车。这辆车由于一些故障不能经过有积水的边。 Yazid 可以在任意节点下车，这样接下来他就可以步行经过有积水的边。但车会被留在他下车的节点并不会再被使用。 需要特殊说明的是，第二天车会被重置，这意味着：

车会在新的出发点被准备好。

Yazid 不能利用之前在某处停放的车。

Yazid 非常讨厌在雨天步行，因此他希望在完成回家这一目标的同时，最小化他步行经过的边的总长度。请你帮助 Yazid 进行计算。 本题的部分测试点将强制在线，具体细节请见【输入格式】和【子任务】。

\(\color{#0066ff}{输入格式}\)

单个测试点中包含多组数据。输入的第一行为一个非负整数T，表示数据的组数。

接下来依次描述每组数据，对于每组数据：

第一行 2 个非负整数 n,m，分别表示节点数、边数。

接下来 m 行，每行 4 个正整数 u,v,l,a，描述一条连接节点 u,v 的、长度为 l、海拔为 a 的边。 在这里，我们保证\(1 \leq u,v \leq n\)。

接下来一行 3 个非负数 Q,K,S ，其中 Q 表示总天数，\(K \in {0,1}\) 是一个会在下面被用到的系数，S 表示的是可能的最高水位线。

接下来 Q 行依次描述每天的状况。每行 2 个整数 \(v_0; p_0\) 描述一天：

这一天的出发节点为\(v = (v_0 + K \times \mathrm{lastans} - 1) \bmod n + 1\)

这一天的水位线为\(p = (p_0 + K \times \mathrm{lastans}) \bmod (S + 1)\)

其中 lastans 表示上一天的答案（最小步行总路程）。特别地，我们规定第 1 天时 lastans = 0。 在这里，我们保证\(1 \leq v_0 \leq n,0 \leq p_0 \leq S\)

对于输入中的每一行，如果该行包含多个数，则用单个空格将它们隔开。

\(\color{#0066ff}{输出格式}\)

依次输出各组数据的答案。对于每组数据：

输出 Q 行每行一个整数，依次表示每天的最小步行总路程。

\(\color{#0066ff}{输入样例}\)

1
4 3
1 2 50 1
2 3 100 2
3 4 50 1
5 0 2
3 0
2 1
4 1
3 1
3 2

\(\color{#0066ff}{输出样例}\)

0
50
200
50
150

\(\color{#0066ff}{数据范围与提示}\)

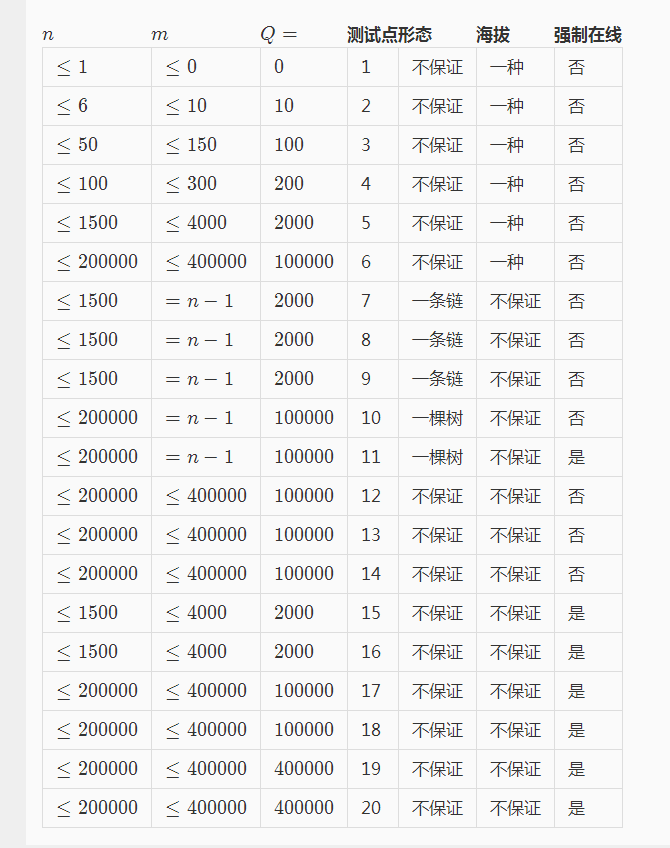
\(\color{#0066ff}{题解}\)

Kruskal重构树

在跑Kruskal的时候，对于加进去的边

建立一个虚点

虚点的点权等于当前边的边权

将虚点与两个并查集的根相连

这样最后会构成一棵树

叶子节点为原来的节点

其余节点为虚点

可以发现这是一个堆

对于本题来说

我们按海拔排序，弄成一个小根堆

对于询问的一个点x

倍增在树上跳到一个最浅的点，使得海拔恰好高于水平面

那么这个点的子树内的所有叶子节点都可以互相到达

我们输出这些叶子节点到1的最短距离即可

这个可以在开始时跑dij预处理

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; int x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 4e5 + 100;
const int inf = 0x7fffffff;
struct E {
	int x, y, z, h;
	const bool operator < (const E &b) const {
		return h > b.h;
	}
}e[maxn];
int r[maxn];
int dep[maxn], f[maxn][26], n, m, min[maxn], val[maxn], ans;
int cnt, dis[maxn];
using std::vector;
using std::pair;
using std::make_pair;
std::priority_queue<pair<int, int>, vector<pair<int, int> >, std::greater<pair<int, int> > > q;
struct node {
	int to, dis;
	node *nxt;
	node(int to = 0, int dis = 0, node *nxt = NULL): to(to), dis(dis), nxt(nxt) {}
	void *operator new (size_t) {
		static node *S = NULL, *T = NULL;
		return (S == T) && (T = (S = new node[1024]) + 1024), S++;
	}
};
node *head[maxn], *h[maxn];
bool vis[maxn];
void add(int from, int to, int dis) {
	h[from] = new node(to, dis, h[from]);
}
void add(int from, int to) {
	head[from] = new node(to, 0, head[from]);
}
void dfs(int x, int fa) {
	f[x][0] = fa;
	dep[x] = dep[fa] + 1;
	for(node *i = head[x]; i; i = i->nxt)
		if(i->to != fa) dfs(i->to, x), min[x] = std::min(min[x], min[i->to]);
}
void dij() {
	for(int i = 1; i <= n; i++) dis[i] = inf, vis[i] = 0;
	q.push(make_pair(dis[1] = 0, 1));
	while(!q.empty()) {
		int tp = q.top().second;
		q.pop();
		if(vis[tp]) continue;
		vis[tp] = true;
		for(node *i = h[tp]; i; i = i->nxt)
			if(dis[i->to] > dis[tp] + i->dis)
				q.push(make_pair(dis[i->to] = dis[tp] + i->dis, i->to));
	}
}
void beizeng() {
	dfs(cnt, 0);
	for(int j = 1; j <= 25; j++)
		for(int i = 1; i <= cnt; i++)
			f[i][j] = f[f[i][j - 1]][j - 1];
}
int findset(int x) { return x == r[x]? r[x] : r[x] = findset(r[x]); }
int query(int x, int y) {
	for(int i = 25; i >= 0; i--) if(val[f[x][i]] > y) x = f[x][i];
	return min[x];
}
void Kruskal() {
	for(int i = 1; i <= n; i++) r[i] = i;
	std::sort(e + 1, e + m + 1);
	int tot = 0;
	cnt = n;
	for(int i = 1; i <= m; i++) {
		int x = findset(e[i].x);
		int y = findset(e[i].y);
		if(x != y) {
			r[x] = r[y] = ++cnt;
			r[cnt] = cnt;
			add(cnt, x);
			add(cnt, y);
			val[cnt] = e[i].h;
			tot++;
		}
		if(tot == n - 1) break;
	}
	for(int i = n + 1; i <= cnt; i++) min[i] = inf;
	beizeng();
	int T = in(), k = in(), s = in();
	int x, y;
	ans = 0;
	while(T --> 0) {
		x = (in() + k * ans - 1) % n + 1;
		y = (in() + k * ans) % (s + 1);
		printf("%d\n", ans = query(x, y));
	}
}
int main() {
	for(int T = in(); T --> 0;) {
		n = in(), m = in();
		memset(head, 0, sizeof head);
		memset(h, 0, sizeof h);
		for(int i = 1; i <= m; i++) {
			E &o = e[i];
			o.x = in(), o.y = in(), o.z = in(), o.h = in();
			add(o.x, o.y, o.z);
			add(o.y, o.x, o.z);
		}
		dij();
		for(int i = 1; i <= n; i++) min[i] = dis[i];
		Kruskal();
	}
	return 0;
}