Computer Vision: Algorithms and ApplicationsのImage processing
实在是太喜欢Richard Szeliski的这本书了。每一章节（after chapter3）都详述了该研究方向比較新的成果。还有很多很多的reference,假设你感兴趣。全然能够看那些參考论文
Point operators(点算子)
Pixel transform(像素变换)
g(x)
= af (x) +b
a和b有时被觉得用来控制对照度和亮度，在我的opencv栏目有个样例是简单的对照度和亮度变换，用的就是这个公式
g(x)
= a(x)f (x)
+ b(x) a,b不一定是常数。能够是空间上的函数
g(x)
= (1 − α)f0(x)
+ αf1(x)
α from0→1 能够实现两幅图像的淡入淡出
在OpenCV里有addWeighted( src1, alpha, src2, beta, 0.0, dst);这个函数，就是实现这个式子的
g(x)
= [f(x)]1/γ
这是伽马校正属于幂变换。通经常使用于图像预处理阶段。对于大多数数字摄像机来说γ≈2.2
除了伽马校正。幂变换在控制对照度也非常实用，能够取不同的γ试一试
除了上面这些，我知道的还有：
g(x) = L -1 -f(x) 灰度级属于[0,L-1] 这是图像反转 可用于增强嵌入与图像暗色区域的白色或灰色细节
g(x) = clog(1+f(x)) 对数变换
Color transform(彩色变换)
好像没有讲什么 ＝ ＝
Compositing and matting(合成与抠图)
C=(1−α)B+αF.
（覆盖算子）
这个算子通过(1−α)因子减弱了背景图像的影响，增加了相应于前景图像的彩色值（和不透明度）
Histogram equalization(直方图均衡化)
public int[][] Histogram_Equalization(int[][] oldmat)
{
int[][] new_mat = new int[height][width];
int[] tmp = new int[256];
for(int i = 0;i < width;i++){
for(int j = 0;j < height;j++){
//System.out.println(oldmat[j][i]);
int index = oldmat[j][i];
tmp[index]++;
}
}
float[] C = new float[256];
int total = width*height;
//计算累积函数
for(int i = 0;i < 256 ; i++){
if(i == 0)
C[i] = 1.0f * tmp[i] / total;
else
C[i] = C[i-1] + 1.0f * tmp[i] / total;
}
for(int i = 0;i < width;i++){
for(int j = 0;j < height;j++){
new_mat[j][i] = (int)(C[oldmat[j][i]] * 255);
new_mat[j][i] = new_mat[j][i] + (new_mat[j][i] << 8) + (new_mat[j][i] << 16);
//System.out.println(new_mat[j][i]);
}
}
return new_mat;
}
这是效果图。能够看到原来的图像被拉伸了
以下是我用Java写的CLAHE.
/*
* CLAHE
* 自适应直方图均衡化
*/
public int[][] AHE(int[][] oldmat,int pblock)
{
int block = pblock;
//将图像均匀分成等矩形大小，8行8列64个块是经常使用的选择
int width_block = width/block;
int height_block = height/block;
//存储各个直方图
int[][] tmp = new int[block*block][256];
//存储累积函数
float[][] C = new float[block*block][256];
//计算累积函数
for(int i = 0 ; i < block ; i ++)
{
for(int j = 0 ; j < block ; j++)
{
int start_x = i * width_block;
int end_x = start_x + width_block;
int start_y = j * height_block;
int end_y = start_y + height_block;
int num = i+block*j;
int total = width_block * height_block;
for(int ii = start_x ; ii < end_x ; ii++)
{
for(int jj = start_y ; jj < end_y ; jj++)
{
int index = oldmat[jj][ii];
tmp[num][index]++;
}
}
//裁剪操作
int average = width_block * height_block / 255;
int LIMIT = 4 * average;
int steal = 0;
for(int k = 0 ; k < 256 ; k++)
{
if(tmp[num][k] > LIMIT){
steal += tmp[num][k] - LIMIT;
tmp[num][k] = LIMIT;
}
}
int bonus = steal/256;
//hand out the steals averagely
for(int k = 0 ; k < 256 ; k++)
{
tmp[num][k] += bonus;
}
//计算累积分布直方图
for(int k = 0 ; k < 256 ; k++)
{
if( k == 0)
C[num][k] = 1.0f * tmp[num][k] / total;
else
C[num][k] = C[num][k-1] + 1.0f * tmp[num][k] / total;
}
}
}
int[][] new_mat = new int[height][width];
//计算变换后的像素值
//依据像素点的位置，选择不同的计算方法
for(int i = 0 ; i < width; i++)
{
for(int j = 0 ; j < height; j++)
{
//four coners
if(i <= width_block/2 && j <= height_block/2)
{
int num = 0;
new_mat[j][i] = (int)(C[num][oldmat[j][i]] * 255);
}else if(i <= width_block/2 && j >= ((block-1)*height_block + height_block/2)){
int num = block*(block-1);
new_mat[j][i] = (int)(C[num][oldmat[j][i]] * 255);
}else if(i >= ((block-1)*width_block+width_block/2) && j <= height_block/2){
int num = block-1;
new_mat[j][i] = (int)(C[num][oldmat[j][i]] * 255);
}else if(i >= ((block-1)*width_block+width_block/2) && j >= ((block-1)*height_block + height_block/2)){
int num = block*block-1;
new_mat[j][i] = (int)(C[num][oldmat[j][i]] * 255);
}
//four edges except coners
else if( i <= width_block/2 )
{
//线性插值
int num_i = 0;
int num_j = (j - height_block/2)/height_block;
int num1 = num_j*block + num_i;
int num2 = num1 + block;
float p = (j - (num_j*height_block+height_block/2))/(1.0f*height_block);
float q = 1-p;
new_mat[j][i] = (int)((q*C[num1][oldmat[j][i]]+ p*C[num2][oldmat[j][i]])* 255);
}else if( i >= ((block-1)*width_block+width_block/2)){
//线性插值
int num_i = block-1;
int num_j = (j - height_block/2)/height_block;
int num1 = num_j*block + num_i;
int num2 = num1 + block;
float p = (j - (num_j*height_block+height_block/2))/(1.0f*height_block);
float q = 1-p;
new_mat[j][i] = (int)((q*C[num1][oldmat[j][i]]+ p*C[num2][oldmat[j][i]])* 255);
}else if( j <= height_block/2 ){
//线性插值
int num_i = (i - width_block/2)/width_block;
int num_j = 0;
int num1 = num_j*block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i*width_block+width_block/2))/(1.0f*width_block);
float q = 1-p;
new_mat[j][i] = (int)((q*C[num1][oldmat[j][i]]+ p*C[num2][oldmat[j][i]])* 255);
}else if( j >= ((block-1)*height_block + height_block/2) ){
//线性插值
int num_i = (i - width_block/2)/width_block;
int num_j = block-1;
int num1 = num_j*block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i*width_block+width_block/2))/(1.0f*width_block);
float q = 1-p;
new_mat[j][i] = (int)((q*C[num1][oldmat[j][i]]+ p*C[num2][oldmat[j][i]])* 255);
}
//inner area
else{
int num_i = (i - width_block/2)/width_block;
int num_j = (j - height_block/2)/height_block;
int num1 = num_j*block + num_i;
int num2 = num1 + 1;
int num3 = num1 + block;
int num4 = num2 + block;
float u = (i - (num_i*width_block+width_block/2))/(1.0f*width_block);
float v = (j - (num_j*height_block+height_block/2))/(1.0f*height_block);
new_mat[j][i] = (int)((u*v*C[num4][oldmat[j][i]] +
(1-v)*(1-u)*C[num1][oldmat[j][i]] +
u*(1-v)*C[num2][oldmat[j][i]] +
v*(1-u)*C[num3][oldmat[j][i]]) * 255);
}
new_mat[j][i] = new_mat[j][i] + (new_mat[j][i] << 8) + (new_mat[j][i] << 16);
}
}
return new_mat;
}Application:Tonal adjustment(色调调整)
Write a simple application to change the color balance of an imageby multiplying each color value by a different user-specified constant. If you want to getfancy, you can make this application
interactive, with sliders.
我仅仅是非常easy地将颜色乘以系数，有slider,比較方便～～
#include "opencv2/highgui/highgui.hpp"
#include <iostream>
using namespace cv;
int alpha = 50;
Mat image,new_image;
static void change_color(int, void*)
{
for( int y = 0; y < image.rows; y++ )
for( int x = 0; x < image.cols; x++ )
for( int c = 0; c < 3; c++ )
new_image.at<Vec3b>(y,x)[c] = saturate_cast<uchar>( alpha/50.0 *( image.at<Vec3b>(y,x)[c] ));
imshow("Image", new_image);
}
int main( int, char** argv )
{
image = imread( argv[1] );
new_image = Mat::zeros( image.size(), image.type() );
namedWindow("Image", 1);
createTrackbar( "pick:", "Image", &alpha, 100, change_color);
change_color(0, 0);
waitKey();
return 0;
}Linear filtering(线性滤波)
与数据列表的卷积.
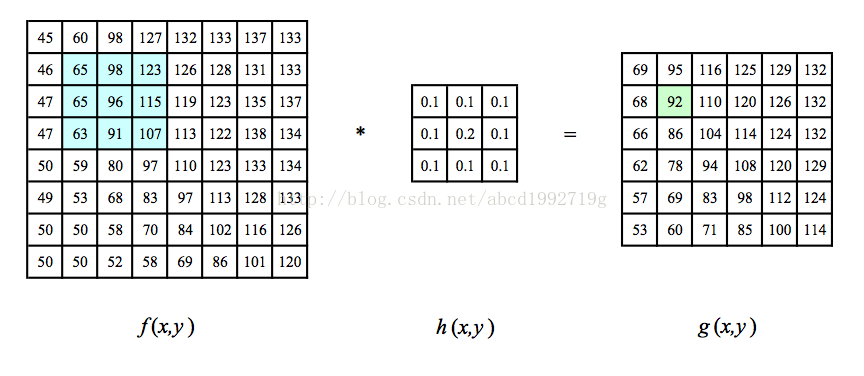
- 0填充，非常easy的处理方式
- 常数填充
- 夹取填塞(clamp)，不断地复制边缘像素的值
- 重叠填塞(wrap)。以环状形态围绕图像进行循环
- 镜像填塞(mirror)，像素围绕图像边界进行镜像反射
- 延长(extend)，通过在边缘像素值中减去镜像信号的方式延长信号
每种模式的公式要我们自己推导（Ex3.8）
Separable filtering(可分离的滤波)
K =vhT
将卷积核K拆分成列向量v和行向量h
用分解的核函数对图像做卷积。
首先，图像的每一行与一维的核kernelX做卷积。然后，运算结果的每一列与一维的核kernelY做卷积。
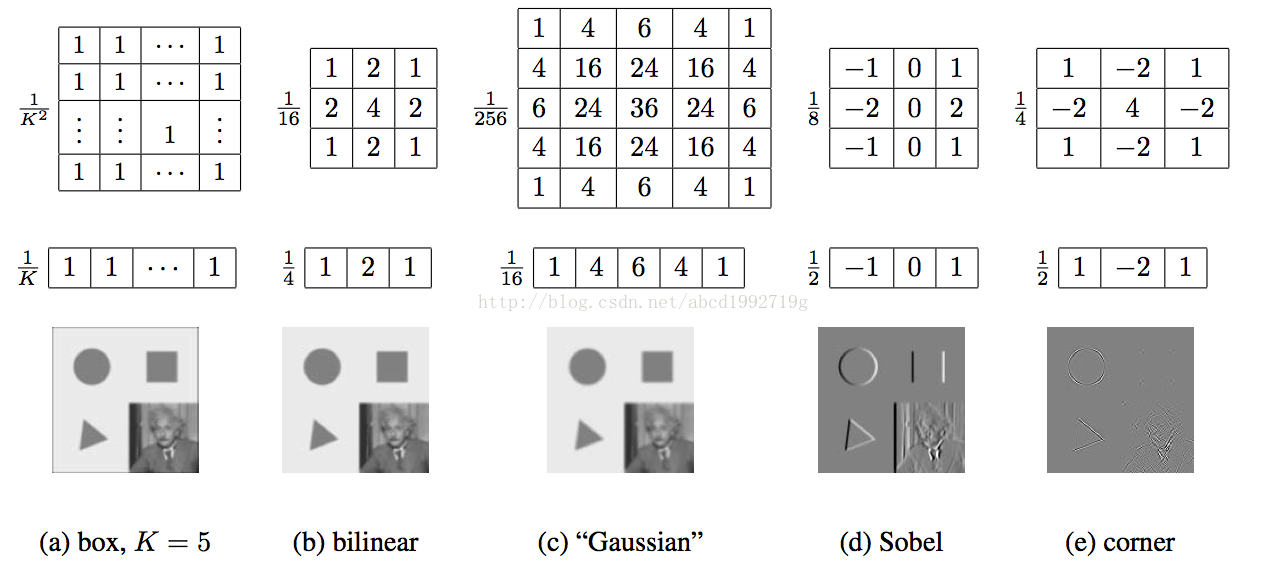
Examples of linear filtering(线性滤波演示样例)
- box，非常easy，就是平均
- bilinear,双线性核
- Gaussian,非常有名，高斯核
- Sobel算子，有效突出水平边缘（拉普拉斯算子也用于边缘提取，canny检測是边缘提取经常使用的算法）
- corner,简单的角点检測器。同一时候寻找水平和垂直方向的二阶导数，这种算子不仅对正方形的角点有响应。并且对沿对角线方向的边缘也有响应
拉普拉斯算子是这种
| 1 | 1 | 1 |
| 1 | -8 | 1 |
| 1 | 1 | 1 |
或者以下
| 0 | 1 | 0 |
| 1 | －4 | 1 |
| 0 | 1 | 0 |
在Opencv里，都有各自相应的函数
就是滑动窗体平均滤波的二维版。
GaussianBlur()
高斯平均。也就是高斯模糊。
medianBlur()
中值滤波，有效去除椒盐噪声。
bilateralFilter()
双线性滤波。
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>
using namespace cv;
int main( int, char** argv )
{
Mat src, src_gray;
Mat grad;
const char* window_name = "Sobel Demo - Simple Edge Detector";
int scale = 1;
int delta = 0;
int ddepth = CV_16S;
/// Load an image
src = imread( argv[1] );
if( !src.data )
{ return -1; }
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
/// Convert it to gray
cvtColor( src, src_gray, CV_RGB2GRAY );
/// Create window
namedWindow( window_name, CV_WINDOW_AUTOSIZE );
/// Generate grad_x and grad_y
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
/// Gradient X
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );
/// Gradient Y
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_y, abs_grad_y );
/// Total Gradient (approximate)
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
imshow( window_name, grad );
waitKey(0);
return 0;
}
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>
using namespace cv;
int main( int, char** argv )
{
Mat src, src_gray, dst;
int kernel_size = 3;
int scale = 1;
int delta = 0;
int ddepth = CV_16S;
const char* window_name = "Laplace Demo";
/// Load an image
src = imread( argv[1] );
if( !src.data )
{ return -1; }
/// Remove noise by blurring with a Gaussian filter
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
/// Convert the image to grayscale
cvtColor( src, src_gray, CV_RGB2GRAY );
/// Create window
namedWindow( window_name, CV_WINDOW_AUTOSIZE );
/// Apply Laplace function
Mat abs_dst;
Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
convertScaleAbs( dst, abs_dst );
/// Show what you got
imshow( window_name, abs_dst );
waitKey(0);
return 0;
}
-1, -1, -1), Point(1,1), 128);
构造了一个例如以下所看到的的核对图像做卷积：
-1 -1 -1
-1 9 -1
-1 -1 -1
核的锚点在(1,1)位置。卷积之后每一个像素加上128.
锚点应该处于核内部。缺省值 (-1,-1) 表示锚点在核中心。
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>
using namespace cv;
int main ( int, char** argv )
{
/// Declare variables
Mat src, dst;
Mat kernel;
Point anchor;
double delta;
int ddepth;
int kernel_size;
const char* window_name = "filter2D Demo";
int c;
/// Load an image
src = imread( argv[1] );
if( !src.data )
{ return -1; }
/// Create window
namedWindow( window_name, CV_WINDOW_AUTOSIZE );
/// Initialize arguments for the filter
anchor = Point( -1, -1 );
delta = 0;
ddepth = -1;
/// Loop - Will filter the image with different kernel sizes each 0.5 seconds
int ind = 0;
for(;;)
{
c = waitKey(500);
/// Press 'ESC' to exit the program
if( (char)c == 27 )
{ break; }
/// Update kernel size for a normalized box filter
kernel_size = 3 + 2*( ind%5 );
kernel = Mat::ones( kernel_size, kernel_size, CV_32F )/ (float)(kernel_size*kernel_size);
/// Apply filter
filter2D(src, dst, ddepth , kernel, anchor, delta, BORDER_DEFAULT );
imshow( window_name, dst );
ind++;
}
return 0;
}Band-pass and steerable filters(带通和导向滤波器)
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWJjZDE5OTI3MTln/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="" />
什么是积分图像？
非常easy发现有 s(i, j)
= s(i−1,
j) +s(i,
j−1)−s(i−1,
j−1) +f(i,
j).
有了sum table后，我们要求(1,1)到(4,4)这个矩形的积分就非常快了。仅仅利用上面4个紫色的点。48+3-13-14 ＝ 24
- 人脸检測利用积分图像来计算简单的多尺度上的底层特征
- 立体视觉和运动算法中差分平方和(SSD)的求和计算
- 可分离的移动平均滤波器
OpenCV有自带的计算积分图的函数integral 提供了很多其它选项，sum是和，sqsum是平方和图像。tilted是旋转45度的和
sum:
the sum summation integral imagesqsum:
the square sum integral imagetilted: image is
rotated by 45 degrees and then its integral is calculated
拭目以待
j) + s(i, j − 1) − s(i − 1,
j − 1) + f(i,
j)是递归滤波器的一个样例
More neighborhood operators(很多其它的领域算子)
Non linear filtering(非线性滤波)
watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvYWJjZDE5OTI3MTln/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="" />
双边滤波器的优点是能够做边缘保存（edge
preserving）。一般过去用的维纳滤波或者高斯滤波去降噪，都会较明显地模糊边缘。对于高频细节的保护效果并不明显。
双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma－d，它是基于空间分布的高斯滤波函数，所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值。这样就保证了边缘附近像素值的保存。可是由于保存了过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，仅仅能够对于低频信息进行较好的滤波
//OpenCV双边滤波
//src:输入图像
//dst:输入图像
//滤波模板半径
//颜色空间标准差
//坐标空间标准差
bilateralFilter(src,dst,5,10.0,2.0);
//关于滤波，还能够參考这里
Iterated adaptive smoothing and anisotropic diffusion(迭代自适应平滑和各向异性扩散)
Morphology(形态学)
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>
using namespace cv;
/// Global variables
Mat src, erosion_dst, dilation_dst;
int erosion_elem = 0;
int erosion_size = 0;
int dilation_elem = 0;
int dilation_size = 0;
int const max_elem = 2;
int const max_kernel_size = 21;
/** Function Headers */
void Erosion( int, void* );
void Dilation( int, void* );
/**
* @function main
*/
int main( int, char** argv )
{
/// Load an image
src = imread( argv[1] );
if( !src.data )
{ return -1; }
/// Create windows
namedWindow( "Erosion Demo", CV_WINDOW_AUTOSIZE );
namedWindow( "Dilation Demo", CV_WINDOW_AUTOSIZE );
cvMoveWindow( "Dilation Demo", src.cols, 0 );
/// Create Erosion Trackbar
createTrackbar( "Element:\n 0: Rect \n 1: Cross \n 2: Ellipse", "Erosion Demo",
&erosion_elem, max_elem,
Erosion );
createTrackbar( "Kernel size:\n 2n +1", "Erosion Demo",
&erosion_size, max_kernel_size,
Erosion );
/// Create Dilation Trackbar
createTrackbar( "Element:\n 0: Rect \n 1: Cross \n 2: Ellipse", "Dilation Demo",
&dilation_elem, max_elem,
Dilation );
createTrackbar( "Kernel size:\n 2n +1", "Dilation Demo",
&dilation_size, max_kernel_size,
Dilation );
/// Default start
Erosion( 0, 0 );
Dilation( 0, 0 );
waitKey(0);
return 0;
}
/**
* @function Erosion
*/
void Erosion( int, void* )
{
int erosion_type = 0;
if( erosion_elem == 0 ){ erosion_type = MORPH_RECT; }
else if( erosion_elem == 1 ){ erosion_type = MORPH_CROSS; }
else if( erosion_elem == 2) { erosion_type = MORPH_ELLIPSE; }
Mat element = getStructuringElement( erosion_type,
Size( 2*erosion_size + 1, 2*erosion_size+1 ),
Point( erosion_size, erosion_size ) );
/// Apply the erosion operation
erode( src, erosion_dst, element );
imshow( "Erosion Demo", erosion_dst );
}
/**
* @function Dilation
*/
void Dilation( int, void* )
{
int dilation_type = 0;
if( dilation_elem == 0 ){ dilation_type = MORPH_RECT; }
else if( dilation_elem == 1 ){ dilation_type = MORPH_CROSS; }
else if( dilation_elem == 2) { dilation_type = MORPH_ELLIPSE; }
Mat element = getStructuringElement( dilation_type,
Size( 2*dilation_size + 1, 2*dilation_size+1 ),
Point( dilation_size, dilation_size ) );
/// Apply the dilation operation
dilate( src, dilation_dst, element );
imshow( "Dilation Demo", dilation_dst );
}开运算
dst=open(src,element)=dilate(erode(src,element),element)
闭运算
dst=close(src,element)=erode(dilate(src,element),element)
形态梯度
dst=morph_grad(src,element)=dilate(src,element)-erode(src,element)
"顶帽"
dst=tophat(src,element)=src-open(src,element)
"黑帽"
dst=blackhat(src,element)=close(src,element)-src
暂时图像 temp 在形态梯度以及对“顶帽”和“黑帽”操作时的 in-place 模式下须要。
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>
using namespace cv;
/// Global variables
Mat src, dst;
int morph_elem = 0;
int morph_size = 0;
int morph_operator = 0;
int const max_operator = 4;
int const max_elem = 2;
int const max_kernel_size = 21;
const char* window_name = "Morphology Transformations Demo";
/** Function Headers */
void Morphology_Operations( int, void* );
/**
* @function main
*/
int main( int, char** argv )
{
/// Load an image
src = imread( argv[1] );
if( !src.data )
{ return -1; }
/// Create window
namedWindow( window_name, CV_WINDOW_AUTOSIZE );
/// Create Trackbar to select Morphology operation
createTrackbar("Operator:\n 0: Opening - 1: Closing \n 2: Gradient - 3: Top Hat \n 4: Black Hat", window_name, &morph_operator, max_operator, Morphology_Operations );
/// Create Trackbar to select kernel type
createTrackbar( "Element:\n 0: Rect - 1: Cross - 2: Ellipse", window_name,
&morph_elem, max_elem,
Morphology_Operations );
/// Create Trackbar to choose kernel size
createTrackbar( "Kernel size:\n 2n +1", window_name,
&morph_size, max_kernel_size,
Morphology_Operations );
/// Default start
Morphology_Operations( 0, 0 );
waitKey(0);
return 0;
}
/**
* @function Morphology_Operations
*/
void Morphology_Operations( int, void* )
{
// Since MORPH_X : 2,3,4,5 and 6
int operation = morph_operator + 2;
Mat element = getStructuringElement( morph_elem, Size( 2*morph_size + 1, 2*morph_size+1 ), Point( morph_size, morph_size ) );
/// Apply the specified morphology operation
morphologyEx( src, dst, operation, element );
imshow( window_name, dst );
}Reference
- Richard Szeliski 《Computer Vision: Algorithms and Applications》
- http://blog.csdn.net/xiaowei_cqu/article/details/7785365
- 《The OpenCV Reference Manual 》 Release 2.4.7
我近期刚開始看Computer Vision: Algorithms and Applications这本书，发现这本书内容非常丰富。这里的文章我也会不断更新，假设你也非常感兴趣，谢谢与我一起讨论^^
Computer Vision: Algorithms and ApplicationsのImage processing的更多相关文章
- [学习笔记] CS131 Computer Vision: Foundations and Applications：Lecture 1 课程介绍
课程大纲:http://vision.stanford.edu/teaching/cs131_fall1718/syllabus.html 课程定位: 课程交叉: what is (computer) ...
- [学习笔记] CS131 Computer Vision: Foundations and Applications：Lecture 2 颜色和数学基础
大纲 what is color? The result of interaction between physical light in the environment and our visual ...
- [学习笔记] CS131 Computer Vision: Foundations and Applications：Lecture 4 像素和滤波器
Background reading: Forsyth and Ponce, Computer Vision Chapter 7 Image sampling and quantization Typ ...
- [学习笔记] CS131 Computer Vision: Foundations and Applications：Lecture 3 线性代数初步
向量和矩阵 什么是矩阵/向量? Vectors and matrix are just collections of ordered numbers that represent something: ...
- [学习笔记] CS131 Computer Vision: Foundations and Applications：Lecture 9 深度学习
深度学习 So far this week Edge detection RANSAC SIFT K-Means Linear classifier Mean-shift PCA/Eigenfaces ...
- Computer Vision: OpenCV, Feature Tracking, and Beyond--From <<Make Things See>> by Greg
In the 1960s, the legendary Stanford artificial intelligence pioneer, John McCarthy, famously gave a ...
- Computer Vision Algorithm Implementations
Participate in Reproducible Research General Image Processing OpenCV (C/C++ code, BSD lic) Image man ...
- Gabor filter for image processing and computer vision
介绍 我们已经知道,傅里叶变换是一种信号处理中的有力工具,可以帮助我们将图像从空域转换到频域,并提取到空域上不易提取的特征.但是经过傅里叶变换后,图像在不同位置的频度特征往往混合在一起,但是Gabor ...
- Computer Vision Tutorials from Conferences (2) -- ECCV
ECCV 2012 (http://eccv2012.unifi.it/program/tutorials/) Vision Applications on Mobile using OpenCVGa ...
随机推荐
- InternalNative.cpp
1 /* * Copyright (C) 2008 The Android Open Source Project * * Licensed under the Apache License, Ver ...
- 【高级功能】使用 Ajax
Ajax 是现代Web 应用程序开发的一项关键工具.它让你能向服务器异步发送和接收数据,然后用 Javascript 解析. Ajax 是 Asynchronous JavaScript and XM ...
- 模拟select控件&&显示单击的坐标&&用户按下键盘，显示keyCode
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...
- windows下简单配置squid反向代理服务器
下载windwosNT版本的squid下载地址: http://squid.acmeconsulting.it/download/squid-2.6.STABLE13-bin.zip 1．把squid ...
- hdu 4601 Letter Tree
不easy啊.. 一个小错误让我wa死了.找了一个晚上,怎么都找不到 最后是对拍代码找到的错误.发现当步数比較小的时候答案就是对的,比較大的时候就不正确了 想到一定是什么地方越界了.. . power ...
- 配置远程maven仓库自己的步骤
---恢复内容开始--- 1.首先在远程服务器配置jdk.maven环境,这个可以在网上找 2.Nexus 安装与配置.这个见网上博客(https://blog.csdn.net/lewis_007/ ...
- shell中的括号作用
一.小括号,圆括号() 1.单小括号 () ①命令组.括号中的命令将会新开一个子shell顺序执行,所以括号中的变量不能够被脚本余下的部分使用.括号中多个命令之间用分号隔开,最后一个命令可以没有 ...
- PHP将多级目录打包成zip文件
最近接触PHP,需要用到zip压缩,在网上搜索的一大堆,发现代码都不低于50行. 而且调用还很费事(基础太少看不懂).让我收获的是Php提供有一个ZipArchive类,并有如下方法. bool a ...
- 给jquery easy-ui 添加右键菜单
版权声明:转自为EasyUI 的Tab 标签添加右键菜单
- ios8 一些运行问题
iOS10相册相机闪退bughttp://www.jianshu.com/p/5085430b029fiOS 10 因苹果健康导致闪退 crashhttp://www.jianshu.com/p/5 ...