HDU-6035：Colorful Tree（虚树+DP）

这里有三道长得像的题：

一：HDU6036：

There is a tree with nn nodes, each of which has a type of color represented by an integer, where the color of node ii is cici.

The path between each two different nodes is unique, of which we define the value as the number of different colors appearing in it.

Calculate the sum of values of all paths on the tree that has n(n−1)/2 paths in total.

InputThe input contains multiple test cases.

For each test case, the first line contains one positive integers nn, indicating the number of node. (2≤n≤200000)(2≤n≤200000)

Next line contains nn integers where the ii-th integer represents cici, the color of node ii. (1≤ci≤n)(1≤ci≤n)

Each of the next n−1n−1 lines contains two positive integers x,yx,y (1≤x,y≤n,x≠y)(1≤x,y≤n,x≠y), meaning an edge between node xx and node yy.

It is guaranteed that these edges form a tree.OutputFor each test case, output " Case #xx: yy" in one line (without quotes), where xxindicates the case number starting from 11 and yy denotes the answer of corresponding case.Sample Input

3
1 2 1
1 2
2 3
6
1 2 1 3 2 1
1 2
1 3
2 4
2 5
3 6

Sample Output

Case #1: 6
Case #2: 29

题意：求出所有路径的颜色种类之和。

二：洛谷P2664

题目描述

lrb有一棵树，树的每个节点有个颜色。给一个长度为n的颜色序列，定义s(i,j) 为i 到j 的颜色数量。以及

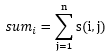
现在他想让你求出所有的sum[i]

输入输出格式

输入格式：

第一行为一个整数n，表示树节点的数量

第二行为n个整数，分别表示n个节点的颜色c[1],c[2]……c[n]

接下来n-1行，每行为两个整数x,y，表示x和y之间有一条边

输出格式：

输出n行，第i行为sum[i]

输入样例#1：

5 
1 2 3 2 3 
1 2 
2 3 
2 4 
1 5

输出样例#1：

10 
9 
11 
9 
12

说明

sum[1]=s(1,1)+s(1,2)+s(1,3)+s(1,4)+s(1,5)=1+2+3+2+2=10 
sum[2]=s(2,1)+s(2,2)+s(2,3)+s(2,4)+s(2,5)=2+1+2+1+3=9 
sum[3]=s(3,1)+s(3,2)+s(3,3)+s(3,4)+s(3,5)=3+2+1+2+3=11 
sum[4]=s(4,1)+s(4,2)+s(4,3)+s(4,4)+s(4,5)=2+1+2+1+3=9 
sum[5]=s(5,1)+s(5,2)+s(5,3)+s(5,4)+s(5,5)=2+3+3+3+1=12

对于40%的数据，n<=2000 
对于100%的数据，1<=n,c[i]<=10^5

 题意：求出每个点到其他点路径的颜色种类和。

三：Wannafly挑战赛19C：多彩的树

有一棵树包含 N 个节点，节点编号从 1 到 N。节点总共有 K 种颜色，颜色编号从 1 到 K。第 i 个节点的颜色为 A_i。
F_i 表示恰好包含 i 种颜色的路径数量。请计算：

输入描述:

第一行输入两个正整数 N 和 K，N 表示节点个数，K 表示颜色种类数量。
第二行输入 N 个正整数， 表示节点的颜色。

接下来 N - 1 行，第 i 行输入两个正整数 U_i 和 V_i，表示节点 U_i 和节点 V_i 之间存在一条无向边，数据保证这 N-1 条边连通了 N 个节点。

1 ≤ N ≤ 50000.
1 ≤ K ≤ 10.
1 ≤ A_i ≤ K.

输出描述:

输出一个整数表示答案。

输入例子:

5 3
1 2 1 2 3
4 2
1 3
2 1
2 5

输出例子:

4600065

-->

示例1

输入

5 3
1 2 1 2 3
4 2
1 3
2 1
2 5

输出

4600065

题意：对于L=[1,K]，统计有多少路径的颜色种类=L；

------------------------------------------分界线-------------------------------------------------

对于第三题，可以容斥搞定。 前面两题可以借助虚树来做。

第三题，容斥，因为K<=10，只有2^K种颜色组合，按照每种颜色组合，用并查集分块。求出块的数量...反正一系列常规操作，最后容斥减去，这里和虚树无关，就不讲了。

第二题，因为要针对每一个点来求，所以考虑虚树加差分。

第一题，因为只计算最后的总结果，所以可以直接一次性操作完。

具体的，对于第二题：对于每种颜色，我们用是这种颜色的点来建立虚树，假设现在按照颜色C得到了一个虚树：虚树的边代表了一个不含颜色C的连通块，还有一些不含颜色C的连通块在虚树的叶子节点下边的连通块和虚树的根的上面的连通块。 对于C颜色对其他点的贡献：颜色是C的点，显然它的结果是N，（即它到每个点的路径都会包含这种颜色）；否则，它的结果是N-所在连通块的大小。 因为一个连通块的结果是相同的，所以我们用差分来统计：即在这个连通块的最高点+ans，所有最低点的儿子-ans，那么求得的前缀和就是结果。            每种颜色都这么干，最后累加一次前缀和，得到每个点的结果。复杂度就是O(N*17)。17是求LCA的复杂度。

对于第一题：可以像第二题那么干，那么ans=(Σ sum[i] )/2。

也可以用更高效的统计方法。 假设有num种颜色，那么初始值为N*(N-1)/2*num，然后对每种颜色，减去没有贡献的部分，同样需要用虚树的思想去想，但是累计的时候一起累计，不必要每种颜色真的去建立虚树，那么一次DFS就可以完事了。

一次DFS，当前节点为u，颜色为C，那么考虑颜色和u相同的这可虚树，u下方是一个颜色非C的连通块，大小为X，这个连通块没有贡献的部分为X*(X-1)/2；（所以就是想象C颜色的虚树），最后C颜色没有统计的部分为虚树的根上面部分，假设虚树的子树大小为sz[root]，没有贡献的部分大小为(N-sz[root])*(N-sz[root]-1)/2；

那么关键就在于如何统计当前C颜色下面非C的连通块大小，用DP的思路去搞就行了。对于子树，每一条链，累加最高的点的子树大小。blabla...

【可以参考】：https://blog.csdn.net/Bahuia/article/details/76141574

第一题代码：没有实际去建虚树，但是有虚树的思想。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=;
int Laxt[maxn],Next[maxn<<],To[maxn<<],vis[maxn];
int a[maxn],col[maxn],sz[maxn],cnt;
ll sum[maxn],ans;
void add(int u,int v) { Next[++cnt]=Laxt[u]; Laxt[u]=cnt; To[cnt]=v; }
void dfs(int u,int f)
{
    ll all=; sz[u]=;
    for(int i=Laxt[u];i;i=Next[i]){
        if(To[i]==f) continue;
        ll pre=sum[col[u]];
        dfs(To[i],u);
        sz[u]+=sz[To[i]];
        ll add=sum[col[u]]-pre; //add的当前颜色的空白连通块大小
        ans-=(ll)(sz[To[i]]-add)*(sz[To[i]]-add-)/;
        all+=sz[To[i]]-add;
    }
    sum[col[u]]+=(ll)all+;
}
int main()
{
    int N,Case=,num,u,v,i,j;
    while(~scanf("%d",&N)){
        memset(Laxt,,sizeof(Laxt));
        memset(sum,,sizeof(sum));
        cnt=; num=; Case++;
        for(i=;i<=N;i++) {
            scanf("%d",&col[i]);
            if(vis[col[i]]!=Case) a[++num]=col[i],vis[col[i]]=Case;
        }
        for(i=;i<N;i++) {
            scanf("%d%d",&u,&v);
            add(u,v); add(v,u);
        }
        ans=(ll)N*(N-1LL)/*num;
        dfs(,);
        for(i=;i<=num;i++) ans-=(N-sum[a[i]])*(N-sum[a[i]]-1LL)/; //减去当前颜色的根是上面连通块
        printf("Case #%d: %lld\n",Case,ans);
    }
    return ;
}