图学java基础篇之集合工具

两个工具类

java.utils下又两个集合相关_(准确来说其中一个是数组的)_的工具类：Arrays和Collections，其中提供了很多针对集合的操作，其中涵盖了一下几个方面：

拷贝、填充、反转等常用的基本操作
排序、查找等算法相关处理
安全性相关处理
类型转换

下边直接用两个图来说明_(其中三言两语说不清的会标红，并在后边打上标记，在图后有对应说明)_：

Arrays

sort中的多种排序算法

印象中JDK很多地方都是快排和归并，这里也不例外，不过这里用的都是优化的算法，并且根据排序元素类型策略不同：

DualPivotQuicksort
- 所有数值基本类型均用此排序，JDK7中新增
- 双基准快速排，改进的多路快排算法
ComparableTimSort
- 默认引用类型均用此排序，JDK7中新增
- 基于TimSort，该算法是优化版本的归并排序，混合使用了归并和插入排序
LegacyMergeSort
- 老版本中的排序算法，JDK7中为兼容仍保留，若想使用可通过-Djava.util.Arrays.useLegacyMergeSort=true
- 优化的归并排序，但是性能较TimSort差

asList需注意的点

asList是我们经常使用的一个方法，可以将一组值直接转成list，但是看下如下代码：

int[] arr = new int[3]{1,2,3};

List list = Arrays.asList(arr);

相信大部分同学初看起来没什么问题吧(反正我一直没觉得有问题)，把数组转成list，然后结果打印list，你会发现其中只有一个元素，这个元素就是arr指向的数组。所以该方法并不能把数组转为list，list的构造函数本身就支持数组，没必要在提供方法

还要注意的一个点是asList返回了一个ArrayList对象，这个对象并不是我们常用的java.utils下的那个，而是Arrays的一个内部类，它是只读的，因此我们要想获得一个不残疾的list，要这样写：

List list = new ArrayListArrays.asList(1,2,3);

hashCode

这个倒没啥好说的，这里直接贴代码吧，主要看下集合的hashCode是怎么计算的。

    public static int hashCode(Object[] var0) {

        if(var0 == null) {

            return 0;

        } else {

            int var1 = 1;

            Object[] var2 = var0;

            int var3 = var0.length;

            for(int var4 = 0; var4 < var3; ++var4) {

                Object var5 = var2[var4];

                var1 = 31 * var1 + (var5 == null?0:var5.hashCode());

            }

            return var1;

        }

    }

deepXXX

就如同拷贝分为深拷贝和浅拷贝一样，由于集合可能是多层的，集合内的元素可能还是一个集合，因此对于集合的很多操作默认是只处理一层，如hashCode、equals、toString，这样对于多层的处理就不是我们期望的结果了。因此Arrays还提供了deepXXX的方法，其会递归的逐层处理。

Collections

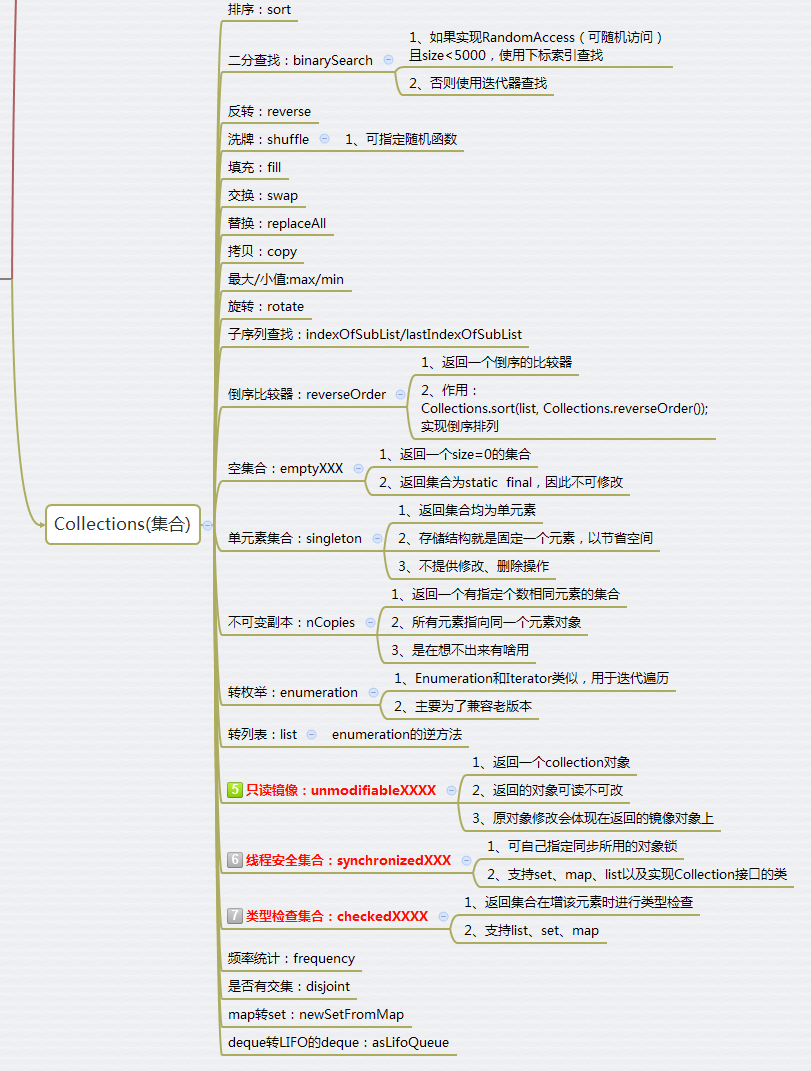
unmodifiableXXXX、synchronizedXXX、checkedXXXX

这三个方法功能各不相同，unmodifiableXXXX返回一个不可修改的副本，synchronizedXXX范围一个线程安全的副本，checkedXXXX返回的副本会对添加操作进行类型检查(这里说副本并不准确，其实操作的还是原对象)，这里之所以要放在一起说，因为他们有很多共同之处：

均使用包装模式实现，将传入对象作为私有属性，然后通过对其操作进行包装实现对应功能
操作的都是原对象，原对象的修改也会体现在包装的对象上
都支持list、set、map

(原图和相关xmind文件见:github)